Giải Bài Tập 1.26 Trang 36 SGK Toán 12 Tập 1

Giải bài tập 1.26 trang 36 SGK Toán 12 tập 1 - Cùng khám phá

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.26 trang 36 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập.

Chúng tôi sẽ cung cấp lời giải bài tập một cách rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.

Người ta cần thiết kế một cái lon có dạng hình trụ có thể tích là 1 lít (Hình 1.41). Tính tỉ lệ chiều cao và bán kính đáy hình trụ này để tổng chi phí làm vỏ lon (bao gồm cả hai đáy) là nhỏ nhất.

Đề bài

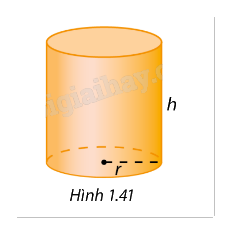
Giải bài tập 1.26 trang 36 SGK Toán 12 tập 1 - Cùng khám phá 1

Phương pháp giải - Xem chi tiết Giải bài tập 1.26 trang 36 SGK Toán 12 tập 1 - Cùng khám phá 2

- Đặt bán kính đáy là 𝑟 và chiều cao là ℎ của hình trụ.

- Tính diện tích toàn phần của hình trụ dựa trên bán kính và chiều cao.

- Viết hàm chi phí cần tối ưu và điều kiện ràng buộc.

- Khảo sát hàm chi phí để tìm giá trị tối ưu.

Lời giải chi tiết

Gọi bán kính đáy là 𝑟 (𝑟 >0) và chiều cao là ℎ (ℎ>0) của hình trụ.

Thể tích hình trụ: \(V = \pi {r^2}h = 1000(c{m^3})\)

Diện tích xung quanh của hình trụ là: \({A_{xq}} = 2\pi rh\)

Diện tích của hai đáy là: \({A_{2đáy}} = 2\pi {r^2}\)

Tổng diện tích bề mặt: \(A = {A_{xq}} + {A_{2d\'a y}} = 2\pi rh + 2\pi {r^2} = 2\pi r.\frac{{1000}}{{\pi {r^2}}} + 2\pi {r^2} = \frac{{2000}}{r} + 2\pi {r^2}\)

Tìm giá trị cực trị: \(f(r) = \frac{{2000}}{r} + 2\pi {r^2}\)

- Tính đạo hàm: \(f'(r) = - \frac{{2000}}{{{r^2}}} + 4\pi r\)

- Cho đạo hàm bằng 0: \( - \frac{{2000}}{{{r^2}}} + 4\pi r = 0 \Rightarrow 4\pi r = \frac{{2000}}{{{r^2}}} \Rightarrow {r^3} = \frac{{2000}}{{4\pi }} = \frac{{500}}{\pi } \Rightarrow r \simeq 5,42(cm)\)

Bảng biến thiên:

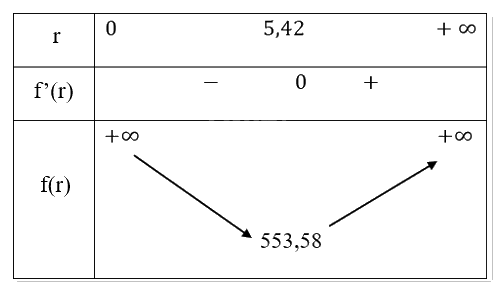
Giải bài tập 1.26 trang 36 SGK Toán 12 tập 1 - Cùng khám phá 3

Nhận thấy f(r) đạt giá trị nhỏ nhất tại r ≈ 5,42

Vậy để tổng chi phí làm vỏ lon nhỏ nhất thì:

- Bán kính đáy của hình trụ: r ≈ 5,42 cm

- Chiều cao của hình trụ: \(h = \frac{{1000}}{{\pi {r^2}}} = \frac{{1000}}{{3,14.{{(5,42)}^2}}} \approx 10,84\)cm

- Tỉ lệ chiều cao và bán kính: \(\frac{h}{r} \approx \frac{{10,84}}{{5,42}} \approx 2\)

Giải Bài Tập 1.26 Trang 36 SGK Toán 12 Tập 1: Chi Tiết và Dễ Hiểu

Bài tập 1.26 trang 36 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học về đạo hàm. Để giải bài tập này, các em cần nắm vững kiến thức về cách tính đạo hàm của hàm số, điều kiện cần và đủ để hàm số đạt cực trị, và cách khảo sát hàm số bằng đạo hàm.

Nội dung bài tập 1.26 trang 36 SGK Toán 12 tập 1

Bài tập yêu cầu các em khảo sát hàm số sau:

f(x) = x³ - 3x² + 2

Các bước giải bài tập 1.26 trang 36 SGK Toán 12 tập 1

Xác định tập xác định của hàm số: Tập xác định của hàm số f(x) = x³ - 3x² + 2 là R (tập hợp tất cả các số thực).
Tính đạo hàm cấp một của hàm số: f'(x) = 3x² - 6x
Tìm điểm dừng của hàm số: Giải phương trình f'(x) = 0 để tìm các điểm dừng.
3x² - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 và x = 2 là các điểm dừng của hàm số.
Xác định dấu của đạo hàm cấp một trên các khoảng xác định:

Khoảng (-∞, 0): f'(x) > 0, hàm số đồng biến.
Khoảng (0, 2): f'(x) < 0, hàm số nghịch biến.
Khoảng (2, +∞): f'(x) > 0, hàm số đồng biến.

Kết luận về cực trị của hàm số:

Tại x = 0, hàm số đạt cực đại và giá trị cực đại là f(0) = 2.
Tại x = 2, hàm số đạt cực tiểu và giá trị cực tiểu là f(2) = -2.

Tính đạo hàm cấp hai của hàm số: f''(x) = 6x - 6
Tìm điểm uốn của hàm số: Giải phương trình f''(x) = 0 để tìm các điểm uốn.
6x - 6 = 0
x = 1
Xác định dấu của đạo hàm cấp hai trên các khoảng xác định:

Khoảng (-∞, 1): f''(x) < 0, hàm số lõm xuống.
Khoảng (1, +∞): f''(x) > 0, hàm số lồi lên.

Kết luận về điểm uốn của hàm số: Tại x = 1, hàm số có điểm uốn và giá trị tại điểm uốn là f(1) = 0.
Vẽ đồ thị hàm số: Dựa vào các kết quả trên, ta có thể vẽ được đồ thị hàm số f(x) = x³ - 3x² + 2.

Lưu ý khi giải bài tập

Khi giải bài tập về khảo sát hàm số bằng đạo hàm, các em cần chú ý:

Xác định đúng tập xác định của hàm số.
Tính đạo hàm chính xác.
Phân tích dấu của đạo hàm để xác định khoảng đồng biến, nghịch biến, cực trị.
Tìm điểm uốn và xác định khoảng lõm, lồi của hàm số.
Vẽ đồ thị hàm số một cách chính xác.

Tusach.vn – Đồng hành cùng học sinh

Tusach.vn hy vọng với lời giải chi tiết và dễ hiểu này, các em sẽ hiểu rõ hơn về cách giải bài tập 1.26 trang 36 SGK Toán 12 tập 1. Hãy truy cập Tusach.vn để tìm kiếm thêm nhiều tài liệu học tập hữu ích khác.

Điểm	Giá trị
Cực đại	(0, 2)
Cực tiểu	(2, -2)
Điểm uốn	(1, 0)
Bảng tóm tắt các điểm đặc biệt của hàm số