Lý thuyết Nguyên hàm Toán 12 Cùng khám phá
Tổng quan nội dung
Lý thuyết Nguyên hàm Toán 12: Nền tảng vững chắc cho tích phân
Nguyên hàm là một khái niệm quan trọng trong chương trình Toán 12, đóng vai trò then chốt trong việc giải quyết các bài toán tích phân. Hiểu rõ lý thuyết nguyên hàm sẽ giúp bạn nắm bắt kiến thức một cách sâu sắc và áp dụng linh hoạt vào các dạng bài tập khác nhau.
Tại tusach.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, chi tiết và dễ hiểu về lý thuyết nguyên hàm, giúp bạn tự tin chinh phục môn Toán.
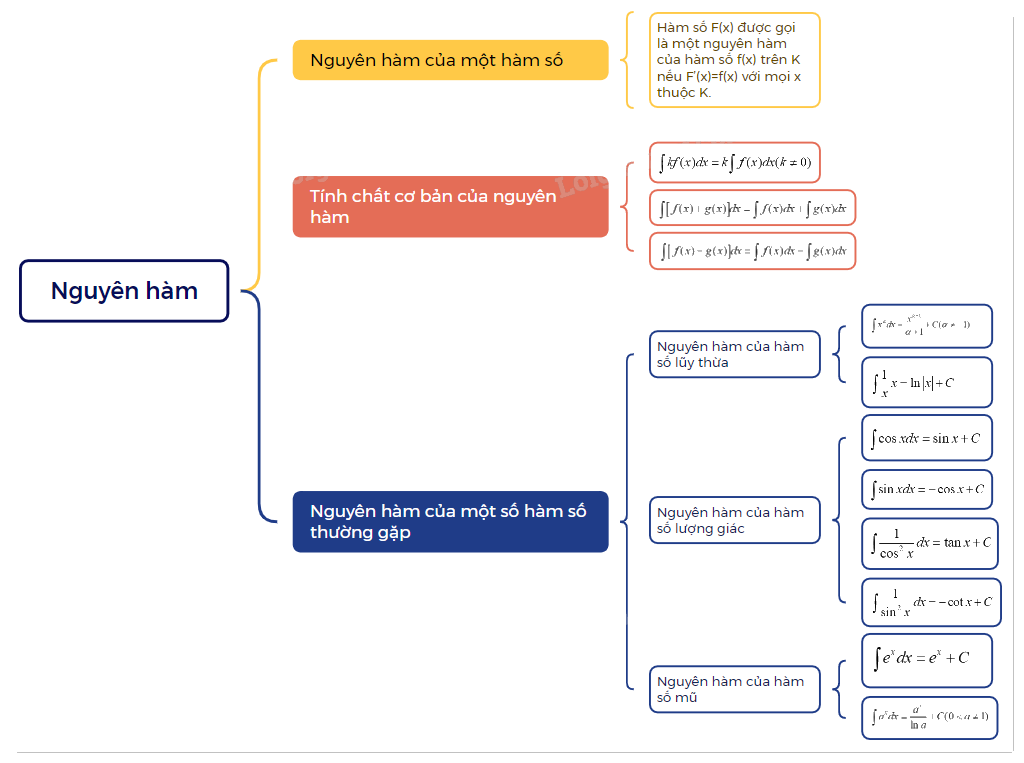
1. Khái niệm nguyên hàm
1. Khái niệm nguyên hàm
| Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x thuộc K. |
Chú ý:
Giả sử hàm số F(x) là một nguyên hàm của f(x) trên K. Khi đó:
a) Với mỗi hằng số C, hàm số F(x) + C cũng là một nguyên hàm của f(x) trên K.
b) Nếu hàm số G(x) là một nguyên hàm của f(x) trên K thì tồn tại một hằng số C sao chp G(x) = F(x) + C với mọi x thuộc K.
Như vậy, nếu F(x) là một nguyên hàm của f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C (C là hằng số). Ta gọi F(x) + với C thuộc R là họ các nguyên hàm của f(x) trên K, kí hiệu \(\int {f(x)dx} = F(x) + C\).
Ví dụ: Chứng minh \(\int {kdx} = kx + C\) với k là hằng số khác 0.
Giải:
Ta có \((kx)' = k\) nên \(F(x) = kx\) là một nguyên hàm của hàm số \(f(x) = k\).
Vậy \(\int {kdx} = kx + C\).
Nhận xét:
Ta có \(\int {0dx} = C\), \(\int {dx} = \int {1dx} = x + C\).
2. Nguyên hàm của một số hàm số thường gặp
Nguyên hàm của hàm số lũy thừa
+ \(\int {{x^\alpha }dx = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C(\alpha \ne - 1)} \) + \(\int {\frac{1}{x}x = \ln \left| x \right| + C} \) |
Ví dụ:
a) \(\int {{x^5}dx} = \frac{1}{6}{x^6} + C\).
b) \(\int {{x^{\sqrt 2 }}dx} = \frac{1}{{\sqrt 2 + 1}}{x^{\sqrt 2 + 1}} + C\).
c) \(\int {{x^{ - 1}}dx} = \int {\frac{1}{x}dx = } \ln \left| x \right| + C\).
Nguyên hàm của hàm số mũ
+ \(\int {{e^x}dx = {e^x} + C} \) + \(\int {{a^x}dx = \frac{{{a^x}}}{{\ln a}} + C(0 < a \ne 1)} \) |
Ví dụ:
a) \(\int {{4^x}dx} = \frac{{{4^x}}}{{\ln 4}} + C\).
b) \(\int {{e^{3x}}dx} = \int {{{\left( {{e^3}} \right)}^x}dx} = \frac{{{{\left( {{e^3}} \right)}^x}}}{{\ln {e^3}}} + C = \frac{1}{3}{e^{3x}} + C\).
c) \(\int {{2^x}{{.3}^x}dx} = \int {{6^x}dx} = \frac{{{6^x}}}{{\ln 6}} + C\).
Nguyên hàm của hàm số lượng giác
+ \(\int {\cos xdx = \sin x + C} \) + \(\int {\sin xdx = - \cos x + C} \) + \(\int {\frac{1}{{{{\cos }^2}x}}dx = \tan x + C} \) + \(\int {\frac{1}{{{{\sin }^2}x}}dx = - \cot x + C} \) |
Ví dụ:
a) \(\int {(1 + {{\tan }^2}x)dx} = \int {\frac{1}{{{{\cos }^2}x}}dx} = \tan x + C\).
b) Tìm nguyên hàm F(x) của hàm số f(x) = sinx, biết \(F(2\pi ) = 0\).
Ta có \(\int {\sin xdx} = - \cos x + C\).
F(x) là nguyên hàm của hàm số f(x) = sinx nên có dạng F(x) = -cosx + C.
Vì \(F(2\pi ) = 0\) nên \( - \cos 2\pi + C = 0\) hay \( - 1 + C = 0\), suy ra C = 1.
Vậy F(x) = 1 – cosx.
3. Tính chất cơ bản của nguyên hàm
Nếu hai hàm số f(x) và g(x) liên tục trên K thì: + \(\int {kf(x)dx = k\int {f(x)dx(k \ne 0)} } \) + \(\int {\left[ {f(x) + g(x)} \right]} dx = \int {f(x)dx + \int {g(x)dx} } \) + \(\int {\left[ {f(x) - g(x)} \right]} dx = \int {f(x)dx - \int {g(x)dx} } \) |
Ví dụ:
a) \(\int {6{x^3}dx} = 6\int {{x^3}dx} = 6.\frac{{{x^4}}}{4} + C = \frac{3}{2}{x^4} + C\).
b) \(\int {(3{x^2} - \cos x)dx} = 3\int {{x^2}dx} - \int {\cos xdx} = {x^3} - \sin x + C\).
c) \(\int {\left( {\frac{2}{{{{\cos }^2}x}} - {5^x}} \right)dx} = 2\int {\frac{1}{{{{\cos }^2}x}}dx} - \int {{5^x}dx} = 2\tan x - \frac{{{5^x}}}{{\ln 5}} + C\).
Lý Thuyết Nguyên Hàm Toán 12: Tổng Quan Chi Tiết
Nguyên hàm là một khái niệm cơ bản nhưng vô cùng quan trọng trong giải tích, đặc biệt là trong chương trình Toán 12. Việc nắm vững lý thuyết nguyên hàm không chỉ giúp bạn giải quyết các bài toán tích phân một cách hiệu quả mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
1. Định Nghĩa Nguyên Hàm
Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên khoảng I nếu F'(x) = f(x) với mọi x thuộc I. Nói cách khác, đạo hàm của nguyên hàm bằng chính hàm số ban đầu.
2. Tính Chất Của Nguyên Hàm
- Nếu F(x) là một nguyên hàm của f(x) thì F(x) + C cũng là một nguyên hàm của f(x), với C là một hằng số bất kỳ.
- Hàm số f(x) có vô số nguyên hàm, chúng khác nhau ở hằng số cộng.
3. Các Công Thức Nguyên Hàm Cơ Bản
Dưới đây là một số công thức nguyên hàm cơ bản mà bạn cần nắm vững:
| Hàm số f(x) | Nguyên hàm F(x) |
|---|---|
| xn (n ≠ -1) | (xn+1)/(n+1) + C |
| 1/x | ln|x| + C |
| ex | ex + C |
| sin(x) | -cos(x) + C |
| cos(x) | sin(x) + C |
4. Phương Pháp Tìm Nguyên Hàm
Có nhiều phương pháp để tìm nguyên hàm, trong đó phổ biến nhất là:
- Phương pháp đặt ẩn phụ: Sử dụng khi biểu thức tích phân có dạng phức tạp, có thể đơn giản hóa bằng cách đặt một ẩn phụ phù hợp.
- Phương pháp tích phân từng phần: Áp dụng khi tích phân của một tích hai hàm số, sử dụng công thức ∫u dv = uv - ∫v du.
- Phương pháp đổi biến số: Sử dụng khi biểu thức tích phân có chứa một hàm số và đạo hàm của nó.
5. Ví Dụ Minh Họa
Ví dụ 1: Tìm nguyên hàm của hàm số f(x) = 2x3 + 3x2 - 1.
Giải:
∫(2x3 + 3x2 - 1) dx = 2∫x3 dx + 3∫x2 dx - ∫1 dx = 2(x4/4) + 3(x3/3) - x + C = x4/2 + x3 - x + C
Ví dụ 2: Tìm nguyên hàm của hàm số f(x) = sin(2x).
Giải:
Đặt u = 2x, du = 2dx => dx = du/2
∫sin(2x) dx = ∫sin(u) (du/2) = (1/2)∫sin(u) du = (1/2)(-cos(u)) + C = -(1/2)cos(2x) + C
6. Ứng Dụng Của Nguyên Hàm
Nguyên hàm có ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
- Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành.
- Tính thể tích vật thể.
- Giải các bài toán vật lý liên quan đến chuyển động và gia tốc.
Hy vọng với những kiến thức về lý thuyết nguyên hàm Toán 12 được trình bày trên đây, bạn sẽ có thêm công cụ để giải quyết các bài toán tích phân một cách hiệu quả. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!