Giải bài tập 2.5 trang 65 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải bài tập 2.5 trang 65 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 2.5 trang 65 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải bài tập hiệu quả.
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G, G' lần lượt là trọng tâm các tam giác ABC và A'B'C'. O là giao điểm của hai đường thẳng AB' và A'B. a) Chứng minh rằng các đường thẳng GO và CG' song song với nhau. b) Tính độ dài của \(\overrightarrow {GO} \)trong trường hợp ABC.A'B'C' là hình lăng trụ đứng, cạnh bên AA' = 3 và đáy là tam giác đều có cạnh bằng 2.
Đề bài
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G, G' lần lượt là trọng tâm các tam giác ABC và A'B'C'. O là giao điểm của hai đường thẳng AB' và A'B.
a) Chứng minh rằng các đường thẳng GO và CG' song song với nhau.
b) Tính độ dài của \(\overrightarrow {GO} \)trong trường hợp ABC.A'B'C' là hình lăng trụ đứng, cạnh bên AA' = 3 và đáy là tam giác đều có cạnh bằng 2.
Phương pháp giải - Xem chi tiết
- Tìm k (k≠0) sao cho \(\overrightarrow {GO} = k\overrightarrow {CG'} \) thì hai đường thẳng GO // CG’ bằng quy tắc trọng tâm tam giác và quy tắc trung điểm của vectơ.
- Tính độ dài của \(\overrightarrow {CG'} \) rồi suy ra độ dài của \(\overrightarrow {GO} \).
Lời giải chi tiết
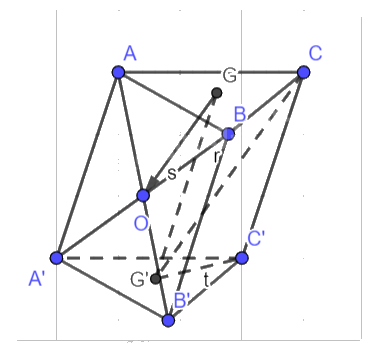
Hình bình hành AA’B’B có O là giao điểm của hai đường chéo nên O là trung điểm của AB’. Do đó: \(2\overrightarrow {GO} = \overrightarrow {GA} + \overrightarrow {GB'} = \overrightarrow {GA} + \overrightarrow {GG'} + \overrightarrow {G'B'} \).
Vì ABC.A’B’C’ là hình lăng trụ có G, G’ lần lượt là trọng tâm của hai đáy nên: \(\overrightarrow {G'B'} = \overrightarrow {GB} ,\overrightarrow {GG'} = \overrightarrow {CC'} ,\overrightarrow {G'C'} = \overrightarrow {GC} \).
Suy ra: \(2\overrightarrow {GO} = \overrightarrow {GA} + \overrightarrow {CC'} + \overrightarrow {GB} = \overrightarrow {GA} + \overrightarrow {CG'} + \overrightarrow {G'C'} + \overrightarrow {GB} = \overrightarrow {GA} + \overrightarrow {CG'} + \overrightarrow {GC} + \overrightarrow {GB} \).
Áp dụng quy tắc trọng tâm của vectơ vào tam giác ABC, ta có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).
Suy ra: \(2\overrightarrow {GO} = \left( {\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GB} } \right) + \overrightarrow {CG'} = \overrightarrow 0 + \overrightarrow {CG'} = \overrightarrow {CG'} \).
Vì tồn tại \(k = \frac{1}{2} \ne 0\) nên GO và CG’ song song với nhau.
b)
Vì ABC.A’B’C’ là hình lăng trụ là lăng trụ đứng nên tam giác CC’G’ vuông tại C’, ta có: \(CG' = \sqrt {CC{'^2} + C'G{'^2}} \).
Mà G’ là trọng tâm của tam giác đều A’B’C’ nên: \(C'G' = \frac{2}{3}.\frac{{\sqrt 3 }}{2}.2 = \frac{{2\sqrt 3 }}{3}\).
Suy ra: \(CG' = \sqrt {{3^2} + {{\left( {\frac{{2\sqrt 3 }}{3}} \right)}^2}} = \frac{{\sqrt {93} }}{3}\).
Từ câu a ta thấy \(\overrightarrow {GO} = \frac{1}{2}\overrightarrow {CG'} \) nên \(\left| {\overrightarrow {GO} } \right| = \frac{1}{2}\left| {\overrightarrow {CG'} } \right| = \frac{1}{2}.\frac{{\sqrt {93} }}{3} = \frac{{\sqrt {93} }}{6}\).
Giải bài tập 2.5 trang 65 SGK Toán 12 tập 1: Tổng quan
Bài tập 2.5 trang 65 SGK Toán 12 tập 1 yêu cầu học sinh vận dụng kiến thức về đạo hàm để khảo sát hàm số bậc ba. Cụ thể, bài toán thường yêu cầu tìm cực trị, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các bước sau:
- Tính đạo hàm bậc nhất (y'): Đạo hàm bậc nhất giúp xác định các điểm cực trị của hàm số.
- Tìm điểm cực trị: Giải phương trình y' = 0 để tìm các điểm cực trị.
- Xác định khoảng đồng biến, nghịch biến: Dựa vào dấu của đạo hàm bậc nhất để xác định khoảng đồng biến và nghịch biến của hàm số.
- Tính đạo hàm bậc hai (y''): Đạo hàm bậc hai giúp xác định tính lồi, lõm của đồ thị hàm số.
- Tìm điểm uốn: Giải phương trình y'' = 0 để tìm các điểm uốn.
- Vẽ đồ thị hàm số: Dựa vào các thông tin đã tìm được để vẽ đồ thị hàm số.
Lời giải chi tiết bài tập 2.5 trang 65 SGK Toán 12 tập 1 (Ví dụ)
Để minh họa, chúng ta sẽ cùng giải một bài tập cụ thể. Giả sử hàm số cần khảo sát là: y = x3 - 3x2 + 2
Bước 1: Tính đạo hàm bậc nhất
y' = 3x2 - 6x
Bước 2: Tìm điểm cực trị
Giải phương trình y' = 0: 3x2 - 6x = 0 => 3x(x - 2) = 0 => x = 0 hoặc x = 2
Vậy hàm số có hai điểm cực trị: x1 = 0 và x2 = 2
Bước 3: Xác định khoảng đồng biến, nghịch biến
- Với x < 0, y' > 0 => Hàm số đồng biến trên khoảng (-∞, 0)
- Với 0 < x < 2, y' < 0 => Hàm số nghịch biến trên khoảng (0, 2)
- Với x > 2, y' > 0 => Hàm số đồng biến trên khoảng (2, +∞)
Bước 4: Tính đạo hàm bậc hai
y'' = 6x - 6
Bước 5: Tìm điểm uốn
Giải phương trình y'' = 0: 6x - 6 = 0 => x = 1
Vậy hàm số có điểm uốn tại x = 1
Bước 6: Vẽ đồ thị hàm số
(Phần này yêu cầu vẽ đồ thị, không thể hiển thị trực tiếp ở đây. Học sinh cần tự vẽ dựa trên các thông tin đã tính toán)
Mẹo giải bài tập khảo sát hàm số
- Nắm vững các công thức đạo hàm cơ bản.
- Thực hành giải nhiều bài tập để làm quen với các dạng bài khác nhau.
- Sử dụng máy tính cầm tay để kiểm tra lại kết quả.
- Chú ý đến các điểm đặc biệt của hàm số như điểm cực trị, điểm uốn, tiệm cận.
Tusach.vn – Nguồn tài liệu học Toán 12 uy tín
Tusach.vn là địa chỉ tin cậy cho các em học sinh cần tìm kiếm tài liệu học Toán 12. Chúng tôi cung cấp đầy đủ các bài giải SGK, bài tập trắc nghiệm, đề thi thử và các tài liệu ôn thi khác. Hãy truy cập Tusach.vn ngay hôm nay để học Toán 12 hiệu quả!
| Dạng bài tập | Phương pháp giải |
|---|---|
| Tìm cực trị | Giải phương trình y' = 0 |
| Xác định khoảng đồng biến, nghịch biến | Xét dấu đạo hàm bậc nhất |
| Tìm điểm uốn | Giải phương trình y'' = 0 |