Giải Bài Tập 4.22 Trang 31 Toán 12 Tập 2

Giải bài tập 4.22 trang 31 SGK Toán 12 tập 2 - Cùng khám phá

Bài tập 4.22 trang 31 SGK Toán 12 tập 2 là một bài toán quan trọng trong chương trình học giải tích lớp 12. Bài tập này thường liên quan đến việc ứng dụng đạo hàm để khảo sát hàm số, tìm cực trị và vẽ đồ thị hàm số.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh nắm vững kiến thức và kỹ năng giải toán.

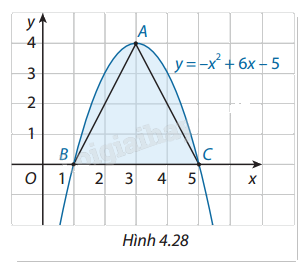
Gọi \((H)\) là hình phẳng giới hạn bởi parabol \(y = - {x^2} + 6x - 5\) và trục hoành. (Hình 4.28) a) Tính diện tích \(S\) của hình \((H)\). b) Từ thế kỉ thứ III trước Công nguyên, khi phép tính tích phân chưa ra đời, Archimedes đã dùng phương pháp của riêng mình và chỉ ra rằng diện tích của hình \((H)\) bằng \(\frac{4}{3}\) lần diện tích tam giác \(ABC\). Tính \(S\) theo kết quả mà Archimedes đã tìm ra và so sánh với kết quả ở câu a.

Đề bài

Gọi \((H)\) là hình phẳng giới hạn bởi parabol \(y = - {x^2} + 6x - 5\) và trục hoành. (Hình 4.28)

a) Tính diện tích \(S\) của hình \((H)\).

b) Từ thế kỉ thứ III trước Công nguyên, khi phép tính tích phân chưa ra đời, Archimedes đã dùng phương pháp của riêng mình và chỉ ra rằng diện tích của hình \((H)\) bằng \(\frac{4}{3}\) lần diện tích tam giác \(ABC\). Tính \(S\) theo kết quả mà Archimedes đã tìm ra và so sánh với kết quả ở câu a.

Giải bài tập 4.22 trang 31 SGK Toán 12 tập 2 - Cùng khám phá 1

Phương pháp giải - Xem chi tiết Giải bài tập 4.22 trang 31 SGK Toán 12 tập 2 - Cùng khám phá 2

Tính diện tích hình phẳng bằng tích phân xác định của hàm \(y = f(x)\) trên đoạn từ giao điểm của parabol với trục hoành.

Bước đầu tiên là tìm nghiệm của phương trình \[y = 0\] (giao điểm với trục hoành).

Sau đó, sử dụng tích phân xác định để tính diện tích hình phẳng.

Diện tích của tam giác \(ABC\) được tính theo công thức diện tích tam giác.

Sau đó, sử dụng kết quả mà Archimedes đã chỉ ra: Diện tích hình \((H)\) bằng \(\frac{4}{3}\) lần diện tích của tam giác \(ABC\)

Lời giải chi tiết

- Phương trình parabol là:

\(y = - {x^2} + 6x - 5.\)

- Tìm nghiệm của phương trình \(y = 0\):

\( - {x^2} + 6x - 5 = 0\quad \Rightarrow \quad x = 1,{\mkern 1mu} x = 5.\)

- Diện tích hình phẳng \(S\) được tính bằng tích phân:

\(S = \int_1^5 {( - {x^2} + 6x - 5)} {\mkern 1mu} dx.\)

Tính tích phân:

\(S = \left[ { - \frac{{{x^3}}}{3} + 3{x^2} - 5x} \right]_1^5 = \left( { - \frac{{125}}{3} + 50} \right) - \left( { - \frac{1}{3} - 2} \right) = \frac{{32}}{3}.\)

Vậy diện tích hình phẳng \(S = \frac{{32}}{3}\).

- Diện tích tam giác \(ABC\) với \(A(3,4)\), \(B(1,0)\), và \(C(5,0)\) là:

\({S_{\Delta ABC}} = \frac{1}{2} \times 4 \times 4 = 8.\)

- Theo Archimedes, diện tích hình \((H)\) bằng \(\frac{4}{3}\) lần diện tích tam giác \(ABC\):

\(S = \frac{4}{3} \times 8 = \frac{{32}}{3}.\)

Kết quả này khớp với kết quả của câu a.

Giải Bài Tập 4.22 Trang 31 Toán 12 Tập 2: Hướng Dẫn Chi Tiết

Bài tập 4.22 trang 31 SGK Toán 12 tập 2 thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các vấn đề liên quan đến hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:

Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
Tính đạo hàm cấp nhất: Sử dụng các quy tắc đạo hàm để tìm đạo hàm f'(x).
Tìm điểm tới hạn: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0 hoặc không xác định.
Khảo sát dấu của đạo hàm: Lập bảng xét dấu f'(x) để xác định khoảng hàm số đồng biến, nghịch biến.
Tìm cực trị: Dựa vào bảng xét dấu đạo hàm để xác định các điểm cực đại, cực tiểu của hàm số.
Tính đạo hàm cấp hai (nếu cần): Sử dụng đạo hàm cấp hai để xác định tính lồi, lõm của đồ thị hàm số và tìm điểm uốn.
Vẽ đồ thị hàm số: Dựa vào các thông tin đã thu thập để vẽ đồ thị hàm số.

Ví dụ minh họa (Giả sử bài tập 4.22 là hàm số y = x^3 - 3x^2 + 2)

Chúng ta sẽ áp dụng các bước trên để giải bài tập này:

Tập xác định: Hàm số xác định trên R.
Đạo hàm cấp nhất: y' = 3x^2 - 6x
Điểm tới hạn: 3x^2 - 6x = 0 => x = 0 hoặc x = 2
Bảng xét dấu đạo hàm:
x -∞ 0 2 +∞
y' + - +
y Đồng biến Nghịch biến Đồng biến
Cực trị:
- x = 0: Điểm cực đại, y = 2
- x = 2: Điểm cực tiểu, y = -2
Đạo hàm cấp hai: y'' = 6x - 6
Điểm uốn: 6x - 6 = 0 => x = 1

x	-∞	0	2	+∞
y'	+	-	+
y	Đồng biến	Nghịch biến	Đồng biến

Lưu ý quan trọng

Luôn kiểm tra lại các bước tính toán để tránh sai sót.
Hiểu rõ ý nghĩa của đạo hàm và các khái niệm liên quan.
Thực hành nhiều bài tập khác nhau để nâng cao kỹ năng giải toán.

Tusach.vn – Đồng hành cùng bạn học Toán 12

Tusach.vn luôn cập nhật lời giải chi tiết các bài tập trong SGK Toán 12 tập 1, tập 2. Chúng tôi hy vọng rằng với những hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc giải bài tập 4.22 trang 31 và các bài tập khác trong chương trình Toán 12. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!