Giải mục 1 trang 51, 52 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 51, 52 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 51, 52 SGK Toán 12 tập 1 tại tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho quá trình học tập của các em, tusach.vn đã biên soạn và trình bày lời giải bài tập một cách rõ ràng, dễ hiểu, kèm theo các lưu ý quan trọng.
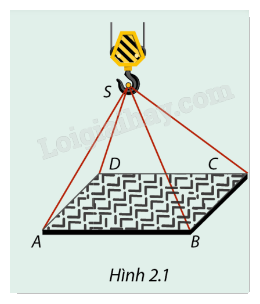
Trên công trường xây dựng, cần cẩu đang đưa một khung thép hình chữ nhật lên tầng cao của tòa nhà. Bốn dây cáp được móc vào bốn đỉnh của khung thép như ở Hình 2.1. Hãy biểu diễn trên hình vẽ hướng của các lực căng của bốn sợi dây cáp này.
LT1
Trả lời câu hỏi Luyện tập 1 trang 52 SGK Toán 12 Cùng khám phá
Cho hình chóp tứ giác S.ABCD. Hãy chỉ ra tất cả những vectơ có điểm đầu và điểm cuối là hai điểm phân biệt lấy trong các điểm S, A, B, C, D.
Phương pháp giải:
Liệt kê tất cả các điểm S, A, B, C, D.
Xác định tất cả các cặp điểm phân biệt có thể chọn từ 5 điểm này.
Từ mỗi cặp điểm, xác định 2 vectơ (một vectơ từ điểm đầu đến điểm cuối và một vectơ từ điểm cuối đến điểm đầu).
Lời giải chi tiết:
Đầu tiên, chúng ta liệt kê tất cả các điểm: S, A, B, C, D.
Bây giờ, chúng ta sẽ xác định tất cả các cặp điểm phân biệt:
1. \(S\) và \(A\): \(\overrightarrow {SA} \), \(\overrightarrow {AS} \)
2. \(S\) và \(B\): \(\overrightarrow {SB} \), \(\overrightarrow {BS} \)
3. \(S\) và \(C\): \(\overrightarrow {SC} \),\(\overrightarrow {CS} \)
4. \(S\) và \(D\): \(\overrightarrow {SD} \),\(\overrightarrow {DS} \)
5. \(A\) và \(B\): \(\overrightarrow {AB} \),\(\overrightarrow {BA} \)
6. \(A\) và \(C\): \(\overrightarrow {AC} \),\(\overrightarrow {CA} \)
7. \(A\) và \(D\): \(\overrightarrow {AD} \),\(\overrightarrow {DA} \)
8. \(B\) và \(C\): \(\overrightarrow {BC} \),\(\overrightarrow {CB} \)
9. \(B\) và \(D\): \(\overrightarrow {BD} \),\(\overrightarrow {DB} \)
10. \(C\) và \(D\): \(\overrightarrow {CD} \),\(\overrightarrow {DC} \)
Tóm lại, có tất cả 20 vectơ có điểm đầu và điểm cuối là hai điểm phân biệt lấy từ các điểm S, A, B, C, D.
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 51 SGK Toán 12 Cùng khám phá
Trên công trường xây dựng, cần cẩu đang đưa một khung thép hình chữ nhật lên tầng cao của tòa nhà. Bốn dây cáp được móc vào bốn đỉnh của khung thép như ở Hình 2.1. Hãy biểu diễn trên hình vẽ hướng của các lực căng của bốn sợi dây cáp này.
Phương pháp giải:
- Xác định các lực căng trong các dây cáp.
- Sử dụng quy tắc hình bình hành để biểu diễn hướng của các lực căng.
- Phân tích lực tác động tại điểm treo S.
Lời giải chi tiết:
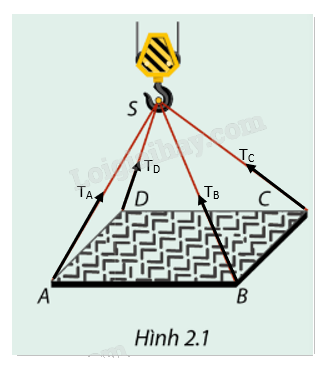
Các dây cáp SA, SB, SC, và SD đều chịu lực căng khi khung thép được nâng lên. Giả sử lực căng trong các dây lần lượt là \({T_A},{T_B},{T_C},{T_D}\).
Biểu diễn hướng của các lực căng:
- Lực căng \({T_A}\) trong dây cáp SA có phương từ điểm A đến điểm S.
- Lực căng \({T_B}\) trong dây cáp SB có phương từ điểm B đến điểm S.
- Lực căng \({T_C}\) trong dây cáp SC có phương từ điểm C đến điểm S.
- Lực căng \({T_D}\) trong dây cáp SD có phương từ điểm D đến điểm S.
Tại điểm S, tổng hợp các lực căng phải cân bằng với lực nâng của cần cẩu. Điều này có nghĩa là tổng hợp của \({T_A},{T_B},{T_C},{T_D}\) phải có phương thẳng đứng và cân bằng với trọng lượng của khung thép.
Trên hình vẽ, các lực căng được biểu diễn như sau:
- \({T_A}\) từ điểm A kéo về phía S.
- \({T_B}\) từ điểm B kéo về phía S.
- \({T_C}\) từ điểm C kéo về phía S.
- \({T_D}\) từ điểm D kéo về phía S.
- HĐ1
- LT1
Trả lời câu hỏi Hoạt động 1 trang 51 SGK Toán 12 Cùng khám phá
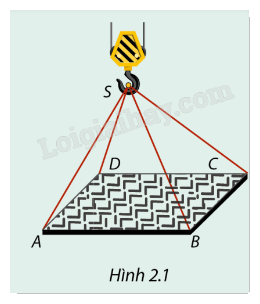
Trên công trường xây dựng, cần cẩu đang đưa một khung thép hình chữ nhật lên tầng cao của tòa nhà. Bốn dây cáp được móc vào bốn đỉnh của khung thép như ở Hình 2.1. Hãy biểu diễn trên hình vẽ hướng của các lực căng của bốn sợi dây cáp này.
Phương pháp giải:
- Xác định các lực căng trong các dây cáp.
- Sử dụng quy tắc hình bình hành để biểu diễn hướng của các lực căng.
- Phân tích lực tác động tại điểm treo S.
Lời giải chi tiết:
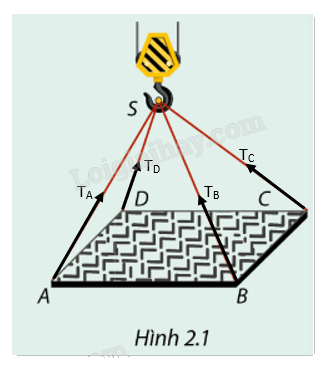
Các dây cáp SA, SB, SC, và SD đều chịu lực căng khi khung thép được nâng lên. Giả sử lực căng trong các dây lần lượt là \({T_A},{T_B},{T_C},{T_D}\).
Biểu diễn hướng của các lực căng:
- Lực căng \({T_A}\) trong dây cáp SA có phương từ điểm A đến điểm S.
- Lực căng \({T_B}\) trong dây cáp SB có phương từ điểm B đến điểm S.
- Lực căng \({T_C}\) trong dây cáp SC có phương từ điểm C đến điểm S.
- Lực căng \({T_D}\) trong dây cáp SD có phương từ điểm D đến điểm S.
Tại điểm S, tổng hợp các lực căng phải cân bằng với lực nâng của cần cẩu. Điều này có nghĩa là tổng hợp của \({T_A},{T_B},{T_C},{T_D}\) phải có phương thẳng đứng và cân bằng với trọng lượng của khung thép.
Trên hình vẽ, các lực căng được biểu diễn như sau:
- \({T_A}\) từ điểm A kéo về phía S.
- \({T_B}\) từ điểm B kéo về phía S.
- \({T_C}\) từ điểm C kéo về phía S.
- \({T_D}\) từ điểm D kéo về phía S.
Trả lời câu hỏi Luyện tập 1 trang 52 SGK Toán 12 Cùng khám phá
Cho hình chóp tứ giác S.ABCD. Hãy chỉ ra tất cả những vectơ có điểm đầu và điểm cuối là hai điểm phân biệt lấy trong các điểm S, A, B, C, D.
Phương pháp giải:
Liệt kê tất cả các điểm S, A, B, C, D.
Xác định tất cả các cặp điểm phân biệt có thể chọn từ 5 điểm này.
Từ mỗi cặp điểm, xác định 2 vectơ (một vectơ từ điểm đầu đến điểm cuối và một vectơ từ điểm cuối đến điểm đầu).
Lời giải chi tiết:
Đầu tiên, chúng ta liệt kê tất cả các điểm: S, A, B, C, D.
Bây giờ, chúng ta sẽ xác định tất cả các cặp điểm phân biệt:
1. \(S\) và \(A\): \(\overrightarrow {SA} \), \(\overrightarrow {AS} \)
2. \(S\) và \(B\): \(\overrightarrow {SB} \), \(\overrightarrow {BS} \)
3. \(S\) và \(C\): \(\overrightarrow {SC} \),\(\overrightarrow {CS} \)
4. \(S\) và \(D\): \(\overrightarrow {SD} \),\(\overrightarrow {DS} \)
5. \(A\) và \(B\): \(\overrightarrow {AB} \),\(\overrightarrow {BA} \)
6. \(A\) và \(C\): \(\overrightarrow {AC} \),\(\overrightarrow {CA} \)
7. \(A\) và \(D\): \(\overrightarrow {AD} \),\(\overrightarrow {DA} \)
8. \(B\) và \(C\): \(\overrightarrow {BC} \),\(\overrightarrow {CB} \)
9. \(B\) và \(D\): \(\overrightarrow {BD} \),\(\overrightarrow {DB} \)
10. \(C\) và \(D\): \(\overrightarrow {CD} \),\(\overrightarrow {DC} \)
Tóm lại, có tất cả 20 vectơ có điểm đầu và điểm cuối là hai điểm phân biệt lấy từ các điểm S, A, B, C, D.
Giải mục 1 trang 51, 52 SGK Toán 12 tập 1: Tổng quan và Phương pháp giải
Mục 1 trang 51, 52 SGK Toán 12 tập 1 thuộc chương trình học về Đạo hàm của hàm số. Đây là một phần kiến thức nền tảng và quan trọng trong chương trình Toán 12, đóng vai trò then chốt trong việc giải quyết các bài toán liên quan đến sự biến thiên của hàm số, cực trị, và ứng dụng của đạo hàm trong các lĩnh vực khác.
Nội dung chính của Mục 1
- Khái niệm đạo hàm: Định nghĩa đạo hàm của hàm số tại một điểm và trên một khoảng.
- Ý nghĩa hình học của đạo hàm: Hệ số góc của tiếp tuyến của đồ thị hàm số tại một điểm.
- Các quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số.
- Đạo hàm của một số hàm số cơ bản: Đạo hàm của hàm số lũy thừa, hàm số mũ, hàm số logarit, hàm số lượng giác.
Hướng dẫn giải chi tiết các bài tập trong Mục 1
Để giúp các em hiểu rõ hơn về cách áp dụng các kiến thức trên vào giải bài tập, tusach.vn xin trình bày lời giải chi tiết cho từng bài tập trong Mục 1 trang 51, 52 SGK Toán 12 tập 1:
Bài 1: Tính đạo hàm của các hàm số sau
a) y = x3 - 2x2 + 5x - 1
Lời giải:
y' = 3x2 - 4x + 5
b) y = (x2 + 1)(x - 2)
Lời giải:
y' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
Bài 2: Cho hàm số y = f(x) = x2. Tính f'(x) và f'(2)
Lời giải:
f'(x) = 2x
f'(2) = 2 * 2 = 4
Bài 3: Tìm hệ số góc của tiếp tuyến của đồ thị hàm số y = x3 tại điểm có hoành độ x = 1
Lời giải:
y' = 3x2
Hệ số góc của tiếp tuyến tại x = 1 là y'(1) = 3 * 12 = 3
Mẹo giải nhanh và hiệu quả
Để giải các bài tập về đạo hàm một cách nhanh chóng và hiệu quả, các em cần nắm vững các quy tắc tính đạo hàm và đạo hàm của các hàm số cơ bản. Ngoài ra, các em cũng nên luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Lưu ý quan trọng
- Luôn kiểm tra lại kết quả sau khi tính đạo hàm.
- Chú ý đến các quy tắc tính đạo hàm của các hàm số phức tạp.
- Hiểu rõ ý nghĩa hình học của đạo hàm để áp dụng vào giải các bài toán liên quan đến tiếp tuyến.
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trong Mục 1 trang 51, 52 SGK Toán 12 tập 1, các em sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ nhé!
Tusach.vn - Đồng hành cùng bạn trên con đường chinh phục kiến thức
Tusach.vn là website học tập trực tuyến uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, và lời giải bài tập cho các môn học từ lớp 6 đến lớp 12. Chúng tôi luôn nỗ lực để mang đến cho các em những trải nghiệm học tập tốt nhất.