Giải mục 2 trang 68, 69, 70 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 68, 69, 70 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết Giải mục 2 trang 68, 69, 70 SGK Toán 12 tập 1. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục 2 trong chương trình Toán 12 tập 1 thường xoay quanh các kiến thức về đạo hàm, ứng dụng đạo hàm để khảo sát hàm số.
Cho điểm trong không gian Oxyz. Trong ba mặt phẳng tọa độ là ba lưới ô vuông có cạnh bằng đơn vị. Biết rằng , và vị trí các điểm M’, A, B, C được cho như trong Hình 2.32. a) Biếu diễn theo hai vecto và . b) Biểu diễn theo hai vecto đơn vị . c) Biểu diễn theo ba vectơ dơn vị .
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 68 SGK Toán 12 Cùng khám phá
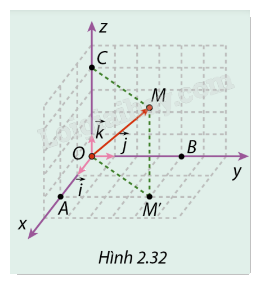
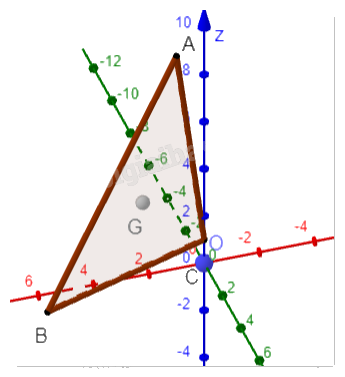
Cho điểm \(M\) trong không gian Oxyz. Trong ba mặt phẳng tọa độ là ba lưới ô vuông có cạnh bằng đơn vị. Biết rằng \(MM' \bot (Oxy)\), \(MC \bot Oz\) và vị trí các điểm M’, A, B, C được cho như trong Hình 2.32.
a) Biểu diễn \(\overrightarrow {OM} \) theo hai vecto \(\overrightarrow {O{M^\prime }} \) và \(\overrightarrow {OC} \).
b) Biểu diễn \(\overrightarrow {O{M^\prime }} \) theo hai vecto đơn vị \(\vec \imath ,\vec \jmath \).
c) Biểu diễn \(\overrightarrow {OM} \) theo ba vectơ dơn vị \(\vec i,\vec j,\vec k\).
Phương pháp giải:
Sử dụng các định nghĩa, các quy tắc về vectơ trong không gian và mối quan hệ trực giao giữa các mặt phẳng tọa độ để biểu diễn các vectơ theo các vectơ đơn vị.
Lời giải chi tiết:
a) Biểu diễn \(\overrightarrow {OM} \) theo hai vectơ \(\overrightarrow {OM'} \) và \(\overrightarrow {OC} \):
Do \(MM' \bot (Oxy)\), \(MC \bot Oz\) nên OCMM’ là hình chữ nhật.
Áp dụng quy tắc hình bình hành vào hình chữ nhật OCMM’, ta có:
\(\overrightarrow {OM} = \overrightarrow {OM'} + \overrightarrow {OC} \)
b) Biểu diễn \(\overrightarrow {OM'} \) theo hai vectơ đơn vị \(\vec i,\vec j\):
Áp dụng quy tắc hình bình hành vào hình chữ nhật OAM’B, ta có:
\(\overrightarrow {OM'} = \overrightarrow {OA} + \overrightarrow {OB} \)
Mà \(\overrightarrow {OA} = 2\overrightarrow i ,\overrightarrow {OB} = 4\overrightarrow j \) nên:
\(\overrightarrow {OM'} = 2\overrightarrow i + 4\overrightarrow j \)
c) Biểu diễn \(\overrightarrow {OM} \) theo ba vectơ đơn vị \(\vec i,\vec j,\vec k\):
Từ câu a, b ta có:
\(\overrightarrow {OM} = \overrightarrow {OM'} + \overrightarrow {OC} \) và \(\overrightarrow {OM'} = 2\overrightarrow i + 4\overrightarrow j \)
Lại có \(\overrightarrow {OC} = 4\overrightarrow k \) nên:
\(\overrightarrow {OM} = 2\vec i + 4\vec j + 4\vec k\)
LT2
Trả lời câu hỏi Luyện tập 2 trang 69 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm A(1;0;9), B(6;1;0) và C(0;0;1). Gọi G là trọng tâm của tam giác ABC. Tìm toạ độ điểm G.
Phương pháp giải:
Trọng tâm của tam giác là trung bình cộng tọa độ của ba đỉnh của tam giác. Nếu các đỉnh của tam giác là \(A({x_1},{y_1},{z_1})\), \(B({x_2},{y_2},{z_2})\), và \(C({x_3},{y_3},{z_3})\), tọa độ của trọng tâm G được tính bằng:
\(G\left( {\frac{{{x_1} + {x_2} + {x_3}}}{3},\frac{{{y_1} + {y_2} + {y_3}}}{3},\frac{{{z_1} + {z_2} + {z_3}}}{3}} \right)\)
Lời giải chi tiết:
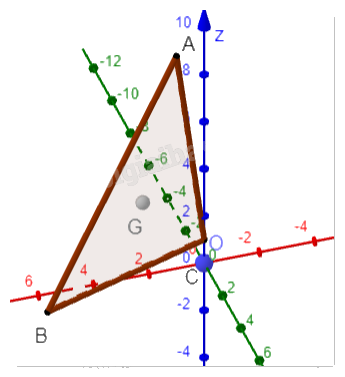
Toạ độ của điểm trọng tâm G là trung bình cộng của toạ độ các điểm A, B, C.
\({x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 + 6 + 0}}{3} = \frac{7}{3}\)
\({y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{0 + 1 + 0}}{3} = \frac{1}{3}\)
\({z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{9 + 0 + 1}}{3} = \frac{{10}}{3}\)
Toạ độ của trọng tâm G là: \(G\left( {\frac{7}{3},\frac{1}{3},\frac{{10}}{3}} \right)\)
LT3
Trả lời câu hỏi Luyện tập 3 trang 70 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có đỉnh A trùng với gốc O, có \[\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AA'} \] theo thứ tự cùng hướng với các vectơ đơn vị \(\vec i,\vec j,\vec k\) và có \(AB = a,AD = b,AA' = c\). Gọi M là trung điểm cạnh CC’. Hãy xác định toạ độ các điểm B, C, C’ và M.
Phương pháp giải:
Xác định tọa độ điểm cơ bản: Sử dụng các vectơ đơn vị để xác định tọa độ của các điểm quan trọng trong không gian.
Xác định tọa độ các điểm còn lại: Tính tọa độ của các điểm đối diện trong hình hộp dựa trên tọa độ của các điểm đã biết.
Tính tọa độ trung điểm: Sử dụng công thức tính trung điểm để tìm tọa độ của điểm trung gian trên cạnh.
Lời giải chi tiết:
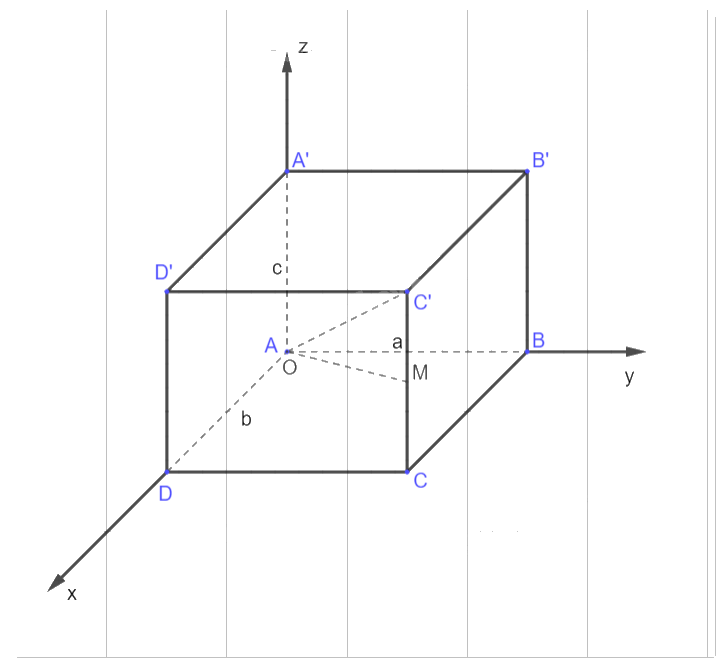
- Xác định tọa độ các điểm cơ bản:
Tọa độ của điểm A là (0, 0, 0) vì A trùng với gốc tọa độ O.
Tọa độ của điểm B: Điểm B nằm cách điểm A một đoạn a theo hướng của vector đơn vị \(\vec i\). Vì vậy, tọa độ của B là (a, 0, 0).
Tọa độ của điểm D: Điểm D nằm cách điểm A một đoạn b theo hướng của vector đơn vị \(\vec j\). Vì vậy, tọa độ của D là (0, b, 0).
Tọa độ của điểm A': Điểm A' nằm cách điểm A một đoạn c theo hướng của vector đơn vị \(\vec k\). Vì vậy, tọa độ của A' là (0, 0, c).
- Xác định tọa độ các điểm còn lại:
Tọa độ của điểm C: Điểm C nằm đối diện với điểm A trong hình hộp và nằm trên mặt phẳng chứa B và D. Vì vậy, tọa độ của C là (a, b, 0).
Tọa độ của điểm C': Điểm C' nằm đối diện với điểm A' trong hình hộp và nằm trên mặt phẳng chứa B' và D'. Vì vậy, tọa độ của C' là (a, b, c).
Trung điểm của đoạn thẳng CC' có tọa độ trung bình của tọa độ C và C'. Tọa độ của C là (a, b, 0) và tọa độ của C' là (a, b, c). Do đó, tọa độ của M là:
\(M = \left( {\frac{{a + a}}{2},\frac{{b + b}}{2},\frac{{0 + c}}{2}} \right) = (a,b,\frac{c}{2})\)
- HĐ2
- LT2
- LT3
Trả lời câu hỏi Hoạt động 2 trang 68 SGK Toán 12 Cùng khám phá
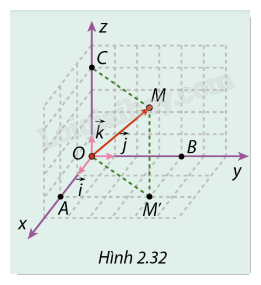
Cho điểm \(M\) trong không gian Oxyz. Trong ba mặt phẳng tọa độ là ba lưới ô vuông có cạnh bằng đơn vị. Biết rằng \(MM' \bot (Oxy)\), \(MC \bot Oz\) và vị trí các điểm M’, A, B, C được cho như trong Hình 2.32.
a) Biểu diễn \(\overrightarrow {OM} \) theo hai vecto \(\overrightarrow {O{M^\prime }} \) và \(\overrightarrow {OC} \).
b) Biểu diễn \(\overrightarrow {O{M^\prime }} \) theo hai vecto đơn vị \(\vec \imath ,\vec \jmath \).
c) Biểu diễn \(\overrightarrow {OM} \) theo ba vectơ dơn vị \(\vec i,\vec j,\vec k\).
Phương pháp giải:
Sử dụng các định nghĩa, các quy tắc về vectơ trong không gian và mối quan hệ trực giao giữa các mặt phẳng tọa độ để biểu diễn các vectơ theo các vectơ đơn vị.
Lời giải chi tiết:
a) Biểu diễn \(\overrightarrow {OM} \) theo hai vectơ \(\overrightarrow {OM'} \) và \(\overrightarrow {OC} \):
Do \(MM' \bot (Oxy)\), \(MC \bot Oz\) nên OCMM’ là hình chữ nhật.
Áp dụng quy tắc hình bình hành vào hình chữ nhật OCMM’, ta có:
\(\overrightarrow {OM} = \overrightarrow {OM'} + \overrightarrow {OC} \)
b) Biểu diễn \(\overrightarrow {OM'} \) theo hai vectơ đơn vị \(\vec i,\vec j\):
Áp dụng quy tắc hình bình hành vào hình chữ nhật OAM’B, ta có:
\(\overrightarrow {OM'} = \overrightarrow {OA} + \overrightarrow {OB} \)
Mà \(\overrightarrow {OA} = 2\overrightarrow i ,\overrightarrow {OB} = 4\overrightarrow j \) nên:
\(\overrightarrow {OM'} = 2\overrightarrow i + 4\overrightarrow j \)
c) Biểu diễn \(\overrightarrow {OM} \) theo ba vectơ đơn vị \(\vec i,\vec j,\vec k\):
Từ câu a, b ta có:
\(\overrightarrow {OM} = \overrightarrow {OM'} + \overrightarrow {OC} \) và \(\overrightarrow {OM'} = 2\overrightarrow i + 4\overrightarrow j \)
Lại có \(\overrightarrow {OC} = 4\overrightarrow k \) nên:
\(\overrightarrow {OM} = 2\vec i + 4\vec j + 4\vec k\)
Trả lời câu hỏi Luyện tập 2 trang 69 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm A(1;0;9), B(6;1;0) và C(0;0;1). Gọi G là trọng tâm của tam giác ABC. Tìm toạ độ điểm G.
Phương pháp giải:
Trọng tâm của tam giác là trung bình cộng tọa độ của ba đỉnh của tam giác. Nếu các đỉnh của tam giác là \(A({x_1},{y_1},{z_1})\), \(B({x_2},{y_2},{z_2})\), và \(C({x_3},{y_3},{z_3})\), tọa độ của trọng tâm G được tính bằng:
\(G\left( {\frac{{{x_1} + {x_2} + {x_3}}}{3},\frac{{{y_1} + {y_2} + {y_3}}}{3},\frac{{{z_1} + {z_2} + {z_3}}}{3}} \right)\)
Lời giải chi tiết:
Toạ độ của điểm trọng tâm G là trung bình cộng của toạ độ các điểm A, B, C.
\({x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 + 6 + 0}}{3} = \frac{7}{3}\)
\({y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{0 + 1 + 0}}{3} = \frac{1}{3}\)
\({z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{9 + 0 + 1}}{3} = \frac{{10}}{3}\)
Toạ độ của trọng tâm G là: \(G\left( {\frac{7}{3},\frac{1}{3},\frac{{10}}{3}} \right)\)
Trả lời câu hỏi Luyện tập 3 trang 70 SGK Toán 12 Cùng khám phá
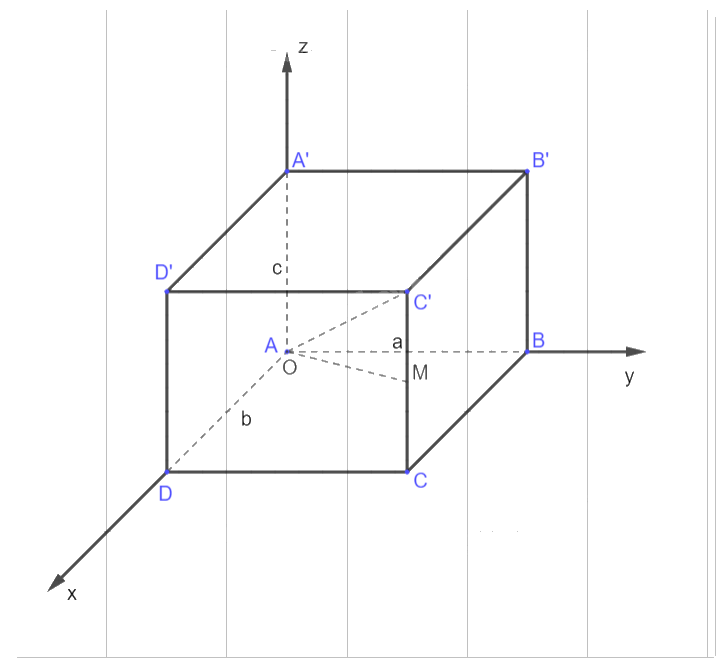
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có đỉnh A trùng với gốc O, có \[\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AA'} \] theo thứ tự cùng hướng với các vectơ đơn vị \(\vec i,\vec j,\vec k\) và có \(AB = a,AD = b,AA' = c\). Gọi M là trung điểm cạnh CC’. Hãy xác định toạ độ các điểm B, C, C’ và M.
Phương pháp giải:
Xác định tọa độ điểm cơ bản: Sử dụng các vectơ đơn vị để xác định tọa độ của các điểm quan trọng trong không gian.
Xác định tọa độ các điểm còn lại: Tính tọa độ của các điểm đối diện trong hình hộp dựa trên tọa độ của các điểm đã biết.
Tính tọa độ trung điểm: Sử dụng công thức tính trung điểm để tìm tọa độ của điểm trung gian trên cạnh.
Lời giải chi tiết:
- Xác định tọa độ các điểm cơ bản:
Tọa độ của điểm A là (0, 0, 0) vì A trùng với gốc tọa độ O.
Tọa độ của điểm B: Điểm B nằm cách điểm A một đoạn a theo hướng của vector đơn vị \(\vec i\). Vì vậy, tọa độ của B là (a, 0, 0).
Tọa độ của điểm D: Điểm D nằm cách điểm A một đoạn b theo hướng của vector đơn vị \(\vec j\). Vì vậy, tọa độ của D là (0, b, 0).
Tọa độ của điểm A': Điểm A' nằm cách điểm A một đoạn c theo hướng của vector đơn vị \(\vec k\). Vì vậy, tọa độ của A' là (0, 0, c).
- Xác định tọa độ các điểm còn lại:
Tọa độ của điểm C: Điểm C nằm đối diện với điểm A trong hình hộp và nằm trên mặt phẳng chứa B và D. Vì vậy, tọa độ của C là (a, b, 0).
Tọa độ của điểm C': Điểm C' nằm đối diện với điểm A' trong hình hộp và nằm trên mặt phẳng chứa B' và D'. Vì vậy, tọa độ của C' là (a, b, c).
Trung điểm của đoạn thẳng CC' có tọa độ trung bình của tọa độ C và C'. Tọa độ của C là (a, b, 0) và tọa độ của C' là (a, b, c). Do đó, tọa độ của M là:
\(M = \left( {\frac{{a + a}}{2},\frac{{b + b}}{2},\frac{{0 + c}}{2}} \right) = (a,b,\frac{c}{2})\)
Giải mục 2 trang 68, 69, 70 SGK Toán 12 tập 1: Tổng quan và hướng dẫn giải chi tiết
Mục 2 của SGK Toán 12 tập 1 tập trung vào việc củng cố và mở rộng kiến thức về đạo hàm, đặc biệt là ứng dụng của đạo hàm trong việc khảo sát hàm số. Việc nắm vững các khái niệm và kỹ năng trong mục này là vô cùng quan trọng, không chỉ cho các bài kiểm tra trong lớp mà còn là nền tảng cho các kiến thức nâng cao hơn trong chương trình học.
Nội dung chính của Mục 2
- Đạo hàm của hàm số: Ôn lại các quy tắc tính đạo hàm cơ bản, đạo hàm của các hàm số lượng giác, hàm số mũ, hàm số logarit.
- Ứng dụng đạo hàm để khảo sát hàm số: Xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn của hàm số.
- Bài tập thực hành: Giải các bài tập vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giải chi tiết các bài tập trang 68, 69, 70
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 2, trang 68, 69, 70 SGK Toán 12 tập 1:
Bài 1: (Trang 68)
Đề bài: (Giả sử đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng)
Bài 2: (Trang 69)
Đề bài: (Giả sử đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng)
Bài 3: (Trang 70)
Đề bài: (Giả sử đề bài cụ thể ở đây)
Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng)
Mẹo giải bài tập về đạo hàm và khảo sát hàm số
- Nắm vững các công thức đạo hàm: Việc thuộc lòng các công thức đạo hàm cơ bản là điều kiện cần thiết để giải quyết các bài tập một cách nhanh chóng và chính xác.
- Sử dụng các phương pháp khảo sát hàm số: Áp dụng các phương pháp như xét dấu đạo hàm, tìm cực trị, điểm uốn để vẽ đồ thị hàm số và phân tích tính chất của hàm số.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập thường gặp.
Tusach.vn – Đồng hành cùng bạn học Toán 12
Tusach.vn tự hào là một trong những trang web cung cấp tài liệu học tập Toán 12 uy tín và chất lượng nhất. Chúng tôi luôn cập nhật những lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và đạt kết quả tốt nhất trong học tập. Ngoài ra, chúng tôi còn cung cấp nhiều tài liệu hữu ích khác như:
- Giải bài tập SGK Toán 12 tập 1, tập 2
- Đề thi thử Toán 12
- Bài giảng Toán 12 online
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chương | Nội dung chính |
|---|---|
| 1 | Hàm số và đạo hàm |
| 2 | Ứng dụng đạo hàm trong khảo sát hàm số |
| Nguồn: SGK Toán 12 tập 1 | |