Đề bài
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau
a) \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên đoạn \([ - 4;1]\)
b) \(y = f(x) = x + \frac{1}{x} - 2\) trên khoảng \(( - \infty ;0)\)
c) \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\) trên nửa khoảng \([2;6)\)
d) \(y = f(x) = \sqrt {4 - {x^2}} \)
e) \(y = f(x) = {e^x} - x\) trên đoạn \([ - 1;2]\)
f) \(y = f(x) = x\ln x\) trên đoạn \([{e^{ - 2}};e]\)
Phương pháp giải - Xem chi tiết
Bước 1 Tính \(f'(x)\)
Bước 2 Lập bảng biến thiên
Bước 3 Tìm cực trị của hàm số trên đoạn
Bước 4 Suy ra điểm có giá trị lớn nhất, điểm có giá trị bé nhất của hàm số trên các khoảng
Lời giải chi tiết
a) \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên đoạn \([ - 4;1]\)
Hàm số trên xác định trên R
Ta có \(f'(x) = {x^2} + 4x + 3\)
Xét \(f'(x) = 0\)
\( \Rightarrow {x^2} + 4x + 3 = 0\) \( \Rightarrow \left[ \begin{array}{l}x = - 1\\x = - 3\end{array} \right.\)
Ta có bảng biến thiên
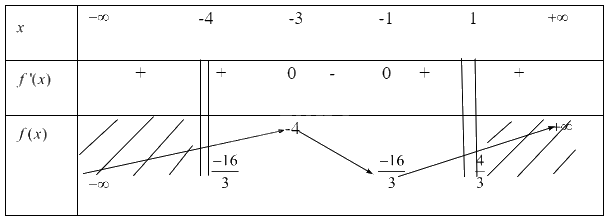
Từ bảng biến thiên ta có
Hàm số \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) đạt GTLN trên đoạn \([ - 4;1]\) tại x = 1 khi đó y = \(\frac{4}{3}\)
Hàm số \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) đạt GTNN trên đoạn \([ - 4;1]\) tại x = -4 và x= -1 khi đó y = \(\frac{{ - 16}}{3}\)
b) \(y = f(x) = x + \frac{1}{x} - 2\) trên khoảng \(( - \infty ;0)\)
Hàm số trên xác định trên R/{0}
Ta có \(f'(x) = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}}\)
Xét \(f'(x) = 0\)
\( \Rightarrow {x^2} - 1 = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Ta có bảng biến thiên
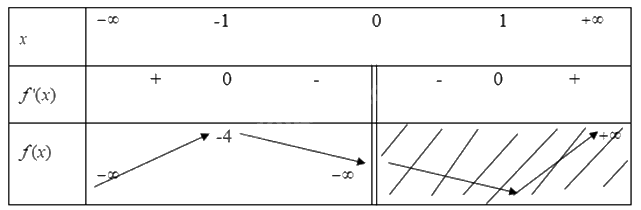
Vậy hàm số \(y = f(x) = x + \frac{1}{x} - 2\) đạt GTLN trên khoảng \(( - \infty ;0)\) tại x=-1 khi đó y=-4
c) \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\) trên nửa khoảng \([2;6)\)
Hàm số xác định trên R/\(\left\{ {\frac{3}{2}} \right\}\)
Ta có \(f'(x) = \frac{1}{{{{(2x - 3)}^2}}}\)
Vì \(f'(x) > 0\) với \(x \in R/\left\{ {\frac{3}{2}} \right\}\)
Nên hàm số luôn đồng biến với \(x \in R/\left\{ {\frac{3}{2}} \right\}\)
Khi đó ta có bảng biến thiên
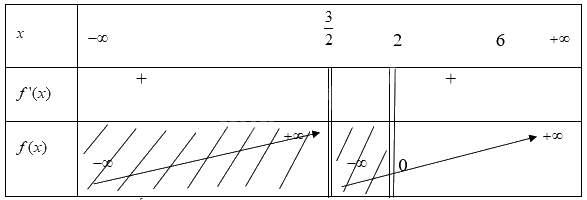
Từ bảng biến thiên ta có:
Hàm số \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\) đạt GTNN trên nửa khoảng \([2;6)\) tại x = 2 khi đó y = 0
d) \(y = f(x) = \sqrt {4 - {x^2}} \)
Hàm số xác định với \(\begin{array}{l}x \in [ - 2;2]\\\end{array}\)
Ta có \(f'(x) = \frac{{ - 2x}}{{2\sqrt {4 - {x^2}} }}\)
Xét \(f'(x) = 0\)\( \Rightarrow x = 0\)
Từ đó ta có bảng biến thiên
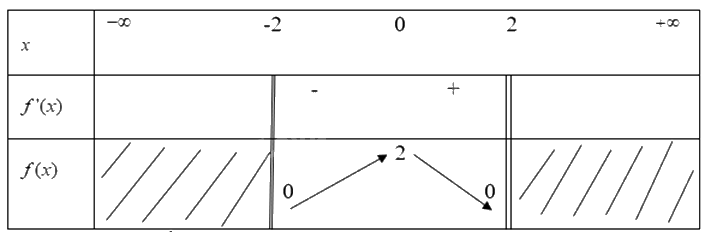
Từ bảng biến thiên, ta có:
Hàm sô \(y = f(x) = \sqrt {4 - {x^2}} \) đạt GTLN tại x = 0 khi đó y =2
Hàm sô \(y = f(x) = \sqrt {4 - {x^2}} \) đạt GTNN tại x = 2 và x= -2 khi đó y =2
e) \(y = f(x) = {e^x} - x\) trên khoảng \([ - 1;2]\)
Hàm số xác định trên R
Ta có \(f'(x) = {e^x} - 1\)
Xét \(f'(x) = 0\)
\( \Rightarrow {e^x} - 1 = 0\)
\( \Rightarrow x = 0\)
Từ đó ta có bảng biến thiên
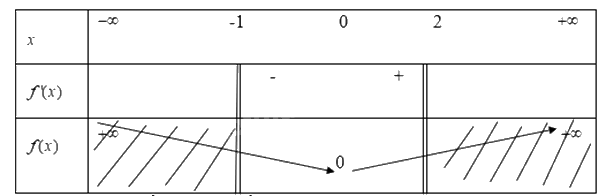
Từ bảng biến thiên ta thấy
Hàm số\(y = f(x) = {e^x} - x\) đạt GTNN trên khoảng\([ - 1;2]\) tại x=0 khi đó y=0
Hàm số\(y = f(x) = {e^x} - x\) đạt GTNN trên khoảng\([ - 1;2]\) tại x=2 khi đó y=5,9
f) \(y = f(x) = x\ln x\) trên khoảng \([{e^{ - 2}};e]\)
Hàm số trên xác định với \(x \in \left( {0; + \infty } \right)\)
Ta có \(f'(x) = \ln x + 1\)
Xét \(f'(x) = \ln x + 1\) \( \Rightarrow x = {e^{ - 1}}\)
Từ đó ta có bảng biến thiên là
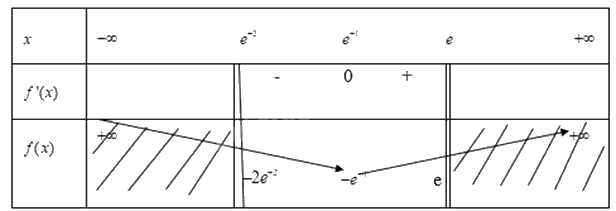
Từ bảng biến thiên ta có:
Hàm số\(y = f(x) = x\ln x\) đạt GTLN trên khoảng \([{e^{ - 2}};e]\) tại x=e khi đó y=e
Hàm số\(y = f(x) = x\ln x\) đạt GTLN trên khoảng \([{e^{ - 2}};e]\) tại x= \({e^{ - 1}}\) khi đó y= \( - {e^{ - 1}}\)
