Giải mục 1 trang 24, 25 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 24, 25 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 24, 25 SGK Toán 12 tập 1. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho hàm số \(y = f(x) = - {x^3} + 3{x^2} - 4\) a) Tập xác định của hàm số \(f(x)\) là gì? b) Hàm số \(f(x)\) đồng biến, nghịch biến trên các khoảng nào? c) Hàm số \(f(x)\) đạt cực đại và cực tiểu tại những điểm nào? d) Đồ thị hàm số \(y = f(x)\) có tiệm cận hay không?
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 24 SGK Toán 12 Cùng khám phá
Cho hàm số \(y = f(x) = - {x^3} + 3{x^2} - 4.\)
a) Tập xác định của hàm số \(f(x)\) là gì?
b) Hàm số \(f(x)\) đồng biến, nghịch biến trên các khoảng nào?
c) Hàm số \(f(x)\) đạt cực đại và cực tiểu tại những điểm nào?
d) Đồ thị hàm số \(y = f(x)\) có tiệm cận hay không?
Phương pháp giải:
a) Tập xác định: Đối với một hàm đa thức, tập xác định là toàn bộ các số thực \(R\).
b) Xét tính đơn điệu:
- Tính \({f^\prime }(x)\).
- Tìm các điểm mà tại đó \({f^\prime }(x)\) bằng 0.
- Lập bảng biến thiên.
c) Tìm cực trị: Từ bảng biến thiên, suy ra các điểm cực trị
d) Tiệm cận: Đối với hàm đa thức, không tồn tại tiệm cận ngang, đứng hay xiên.
Lời giải chi tiết:
a) Hàm số \(f(x) = - {x^3} + 3{x^2} - 4\) là một đa thức bậc ba, nên D=R.
b) Xét tính đơn điệu
Tính \({f^\prime }(x):{f^\prime }(x) = - 3{x^2} + 6x\)
Tìm nghiệm khi \({f^\prime }(x) = 0\)
\({f^\prime }(x) = 0 \leftrightarrow - 3{x^2} + 6x = 0\)
\( \leftrightarrow - 3x(x - 2) = 0\)
\( \leftrightarrow x = 0\)hoặc \(x = 2\)
Tính giới hạn
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \left( { - {x^3} + 3{x^2} - 4} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ { - {x^3}\left( {1 + \frac{3}{x} - \frac{4}{{{x^3}}}} \right)} \right] = - \infty \\\end{array}\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 3{x^2} - 4} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ { - {x^3}\left( {1 + \frac{3}{x} - \frac{4}{{{x^3}}}} \right)} \right] = + \infty \)
Bảng biến thiên:
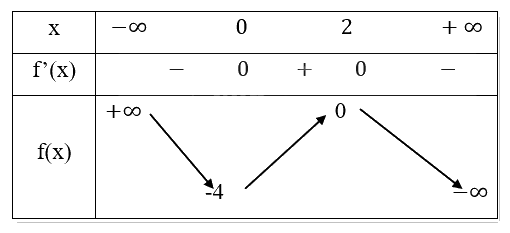
Kết luận:
- Hàm số nghịch biến trên các khoảng \(( - \infty ;0)\) và \((2; + \infty )\).
- Hàm số đồng biến trên khoảng \((0;2)\).
c) Tìm cực trị
Dựa vào bảng biến thiên, ta có thể kết luận:
- Hàm số đạt cực tiểu tại \(x = 0\)
- Hàm số đạt cực đại tại \(x = 2\)
d) Hàm số \(f(x)\) là một đa thức bậc ba, vì vậy nó không có tiệm cận ngang, đứng hay xiên. Đồ thị của hàm số không có tiệm cận.
- HĐ1
Trả lời câu hỏi Hoạt động 1 trang 24 SGK Toán 12 Cùng khám phá
Cho hàm số \(y = f(x) = - {x^3} + 3{x^2} - 4.\)
a) Tập xác định của hàm số \(f(x)\) là gì?
b) Hàm số \(f(x)\) đồng biến, nghịch biến trên các khoảng nào?
c) Hàm số \(f(x)\) đạt cực đại và cực tiểu tại những điểm nào?
d) Đồ thị hàm số \(y = f(x)\) có tiệm cận hay không?
Phương pháp giải:
a) Tập xác định: Đối với một hàm đa thức, tập xác định là toàn bộ các số thực \(R\).
b) Xét tính đơn điệu:
- Tính \({f^\prime }(x)\).
- Tìm các điểm mà tại đó \({f^\prime }(x)\) bằng 0.
- Lập bảng biến thiên.
c) Tìm cực trị: Từ bảng biến thiên, suy ra các điểm cực trị
d) Tiệm cận: Đối với hàm đa thức, không tồn tại tiệm cận ngang, đứng hay xiên.
Lời giải chi tiết:
a) Hàm số \(f(x) = - {x^3} + 3{x^2} - 4\) là một đa thức bậc ba, nên D=R.
b) Xét tính đơn điệu
Tính \({f^\prime }(x):{f^\prime }(x) = - 3{x^2} + 6x\)
Tìm nghiệm khi \({f^\prime }(x) = 0\)
\({f^\prime }(x) = 0 \leftrightarrow - 3{x^2} + 6x = 0\)
\( \leftrightarrow - 3x(x - 2) = 0\)
\( \leftrightarrow x = 0\)hoặc \(x = 2\)
Tính giới hạn
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \left( { - {x^3} + 3{x^2} - 4} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ { - {x^3}\left( {1 + \frac{3}{x} - \frac{4}{{{x^3}}}} \right)} \right] = - \infty \\\end{array}\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 3{x^2} - 4} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ { - {x^3}\left( {1 + \frac{3}{x} - \frac{4}{{{x^3}}}} \right)} \right] = + \infty \)
Bảng biến thiên:
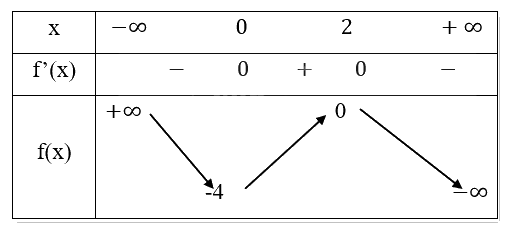
Kết luận:
- Hàm số nghịch biến trên các khoảng \(( - \infty ;0)\) và \((2; + \infty )\).
- Hàm số đồng biến trên khoảng \((0;2)\).
c) Tìm cực trị
Dựa vào bảng biến thiên, ta có thể kết luận:
- Hàm số đạt cực tiểu tại \(x = 0\)
- Hàm số đạt cực đại tại \(x = 2\)
d) Hàm số \(f(x)\) là một đa thức bậc ba, vì vậy nó không có tiệm cận ngang, đứng hay xiên. Đồ thị của hàm số không có tiệm cận.
Giải mục 1 trang 24, 25 SGK Toán 12 tập 1: Tổng quan và Phương pháp giải
Mục 1 trang 24, 25 SGK Toán 12 tập 1 thường xoay quanh các kiến thức cơ bản về đạo hàm, bao gồm định nghĩa, ý nghĩa hình học của đạo hàm, các quy tắc tính đạo hàm của hàm số đơn giản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit. Việc nắm vững các khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình Toán 12.
Nội dung chi tiết Giải mục 1 trang 24, 25
Để giúp các em hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết từng bài tập trong mục này. Lưu ý rằng, trước khi bắt đầu giải, các em nên ôn lại lý thuyết và các công thức đạo hàm cơ bản.
Bài 1: Tính đạo hàm của các hàm số sau
- f(x) = x3 - 2x2 + 5x - 1
- g(x) = sin(x) + cos(x)
- h(x) = ex + ln(x)
Hướng dẫn giải:
- Áp dụng quy tắc đạo hàm của tổng, hiệu, tích, thương.
- Sử dụng các công thức đạo hàm cơ bản: (xn)' = nxn-1, (sin(x))' = cos(x), (cos(x))' = -sin(x), (ex)' = ex, (ln(x))' = 1/x.
Bài 2: Tìm đạo hàm của hàm số y = (x2 + 1) / (x - 1)
Hướng dẫn giải:
Sử dụng quy tắc đạo hàm của thương: (u/v)' = (u'v - uv') / v2, với u = x2 + 1 và v = x - 1.
Bài 3: Tính đạo hàm cấp hai của hàm số f(x) = x4 - 3x2 + 2
Hướng dẫn giải:
Đạo hàm cấp hai là đạo hàm của đạo hàm cấp một. Tức là, f''(x) = (f'(x))'.
Lưu ý quan trọng khi giải bài tập về đạo hàm
- Nắm vững các công thức đạo hàm cơ bản.
- Áp dụng đúng các quy tắc đạo hàm.
- Kiểm tra lại kết quả sau khi tính toán.
- Thực hành thường xuyên để làm quen với các dạng bài tập khác nhau.
Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn không chỉ cung cấp lời giải chi tiết các bài tập trong SGK mà còn tổng hợp nhiều tài liệu ôn tập, đề thi thử, và các bài giảng video chất lượng cao. Chúng tôi luôn cố gắng mang đến cho các em những trải nghiệm học tập tốt nhất.
Bảng tổng hợp công thức đạo hàm cơ bản
| Hàm số | Đạo hàm |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sin(x) | y' = cos(x) |
| y = cos(x) | y' = -sin(x) |
| y = ex | y' = ex |
| y = ln(x) | y' = 1/x |
Hy vọng với những hướng dẫn chi tiết này, các em sẽ tự tin hơn khi giải các bài tập về đạo hàm trong SGK Toán 12 tập 1. Chúc các em học tập tốt!