Giải mục 2 trang 89, 90, 91, 92, 93 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 89, 90, 91, 92, 93 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 89, 90, 91, 92, 93 SGK Toán 12 tập 1 trên tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho các em trong quá trình học tập, tusach.vn đã biên soạn và trình bày lời giải bài tập một cách rõ ràng, dễ hiểu, kèm theo các lưu ý quan trọng.
Trở lại với bảng 3.1 về khối lượng của 100 quả dứa giống E. Để tiện tính toán, ta biểu diễn dữ liệu bằng một bảng hai cột như bảng trên. a) Hãy tính các tứ phân vị của mẫu số liệu cho trong bảng. b) Đề xuất một cách ước tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho.
LT3
Trả lời câu hỏi Luyện tập 3 trang 92 SGK Toán 12 Cùng khám phá
Ở một phòng điều trị nội trú của bệnh viện, dữ liệu thống kê thời gian ngủ hằng đêm của hai bệnh nhân trong suốt một tháng được tổng hợp bởi hai bảng dưới đây:
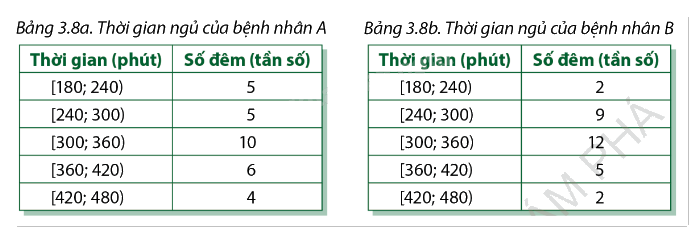
Bệnh nhân nào có thời gian ngủ ổn định hơn?
Phương pháp giải:
Tính tần suất tích lũy cho cả hai bệnh nhân.
Xác định \({Q_1}\), \({Q_2}\), và \({Q_3}\) cho mỗi bệnh nhân.
Tính khoảng tứ phân vị \({\Delta _Q}\) cho mỗi bệnh nhân.
So sánh khoảng tứ phân vị \({\Delta _Q}\) của hai bệnh nhân. Bệnh nhân có \({\Delta _Q}\) nhỏ hơn sẽ có thời gian ngủ ổn định hơn.
Lời giải chi tiết:
- Bệnh nhân A:
Tính tần suất tích luỹ:
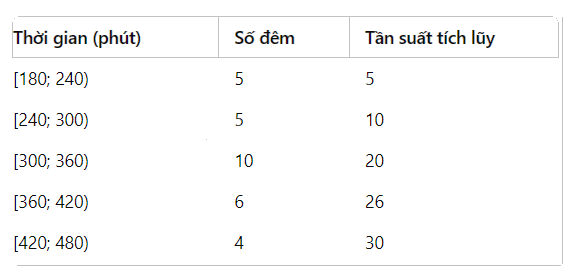
Tính tứ phân vị:
\({Q_1} = 240 + \frac{{7.5 - 5}}{5} \times 60 = 240 + 30 = 270\) phút
\({Q_2} = 300 + \frac{{15 - 10}}{{10}} \times 60 = 300 + 30 = 330\) phút
\({Q_3} = 360 + \frac{{22.5 - 20}}{6} \times 60 = 360 + 25 = 385\) phút
Khoảng tứ phân vị là:
\(\Delta _Q^A = {Q_3} - {Q_1} = 385 - 270 = 115\) phút
- Bệnh nhân B:
Tính tần suất tích luỹ:
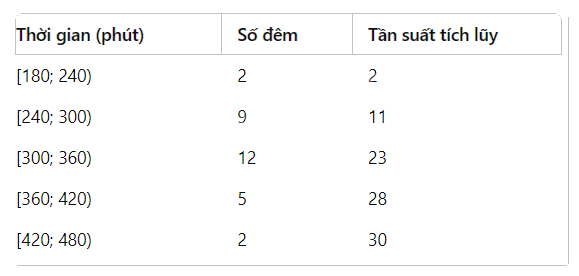
Tính tứ phân vị:
\({Q_1} = 240 + \frac{{7.5 - 2}}{9} \times 60 = 240 + 36,67 = 276,67\) phút
\({Q_2} = 300 + \frac{{15 - 11}}{{12}}.60 = 320\) phút
\({Q_3} = 300 + \frac{{22.5 - 11}}{{12}} \times 60 = 300 + 57,5 = 357,5\) phút
Khoảng tứ phân vị là:
\(\Delta _Q^B = {Q_3} - {Q_1} = 357.5 - 276.67 = 80.83\) phút
Vì \(\Delta _Q^B < \Delta _Q^A\) nên bệnh nhân B có thời gian ngủ ổn định hơn.
LT4
Trả lời câu hỏi Luyện tập 4 trang 93 SGK Toán 12 Cùng khám phá
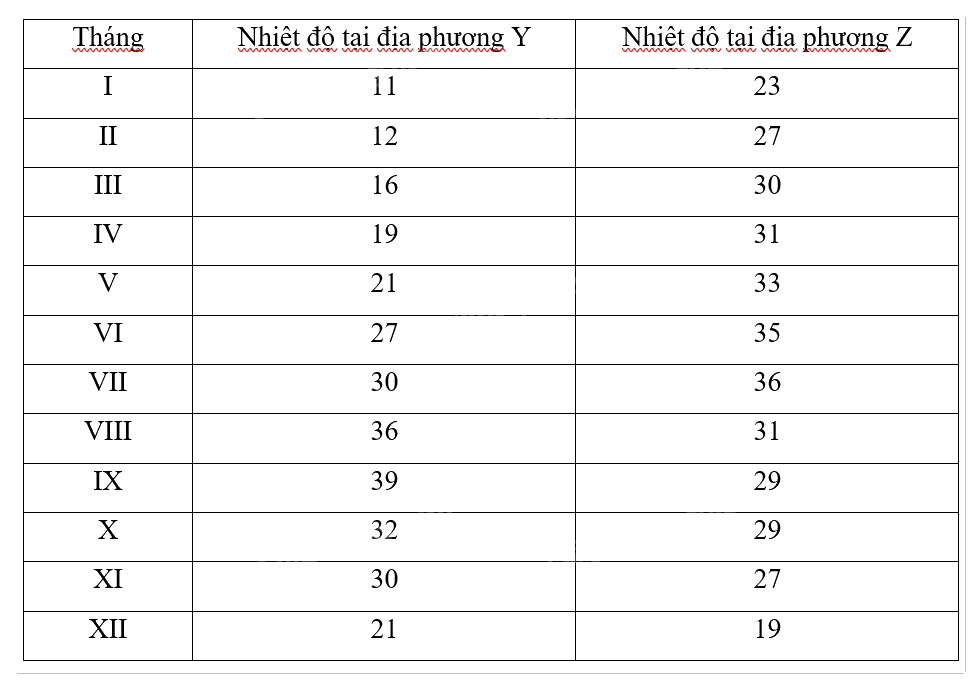
Hình 3.3 là biểu đồ biểu diễn nhiệt độ trung bình hằng tháng của hai địa phương Y, Z.
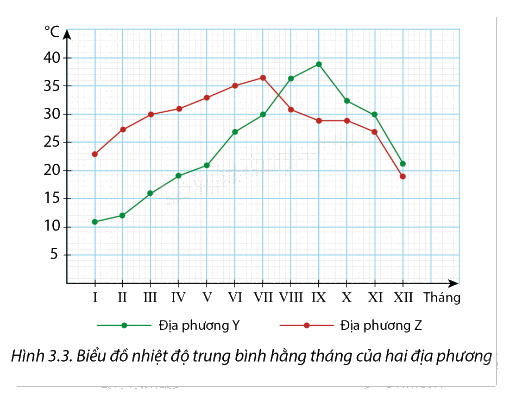
a) Lập bảng số liệu ghép nhóm về nhiệm độ của hai địa phương Y, Z, với độ dài các nhóm là 5 và đầu mút phải của nhóm cuối cùng là 40.
b) Tìm khoảng tứ phân vị của nhiệt độ mỗi địa phương và cho biết nhiệt độ của địa phương nào ít biến động hơn.
Phương pháp giải:
a)
- Tạo bảng với các hàng tương ứng với các khoảng nhiệt độ (5-10, 10-15, ..., 35-40) và hai cột tương ứng với địa phương Y và Z.
- Đếm số lượng tháng mà nhiệt độ trung bình rơi vào mỗi khoảng nhiệt độ cho từng địa phương.
b)
- Xác định khoảng tứ phân vị.
- Địa phương nào có khoảng tứ phân vị nhỏ hơn thì nhiệt độ của địa phương đó biến động ít hơn.
Lời giải chi tiết:
Đọc số liệu từ biểu đồ:
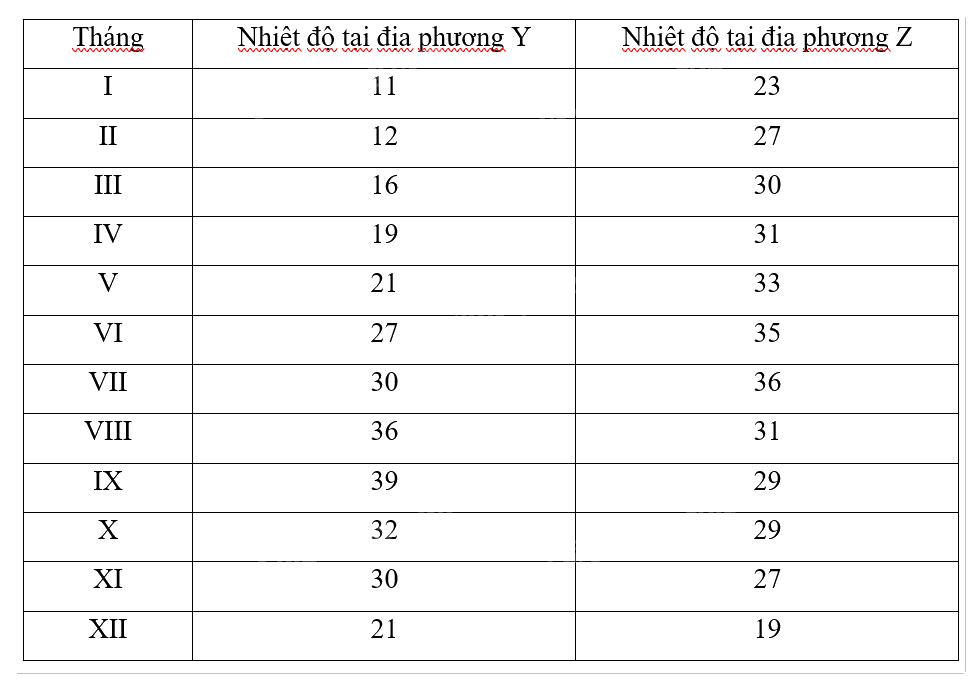
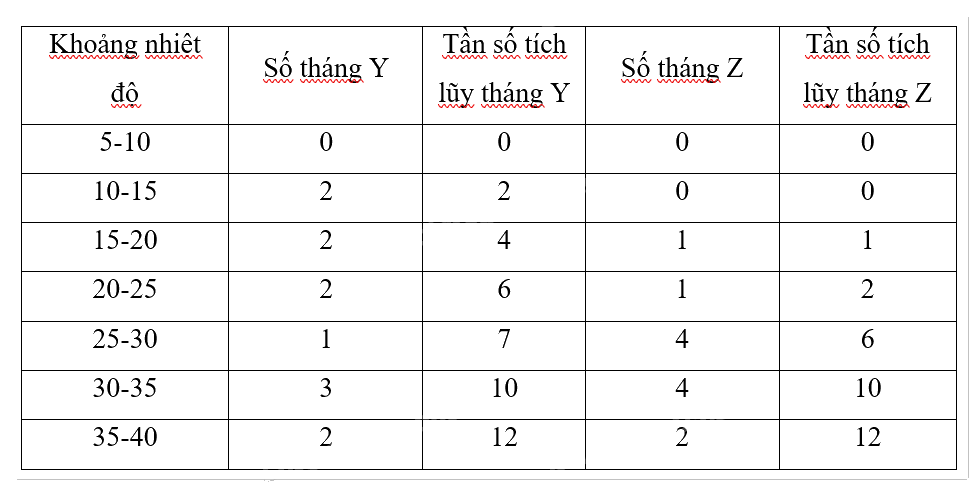
Lập bảng số liệu ghép nhóm:
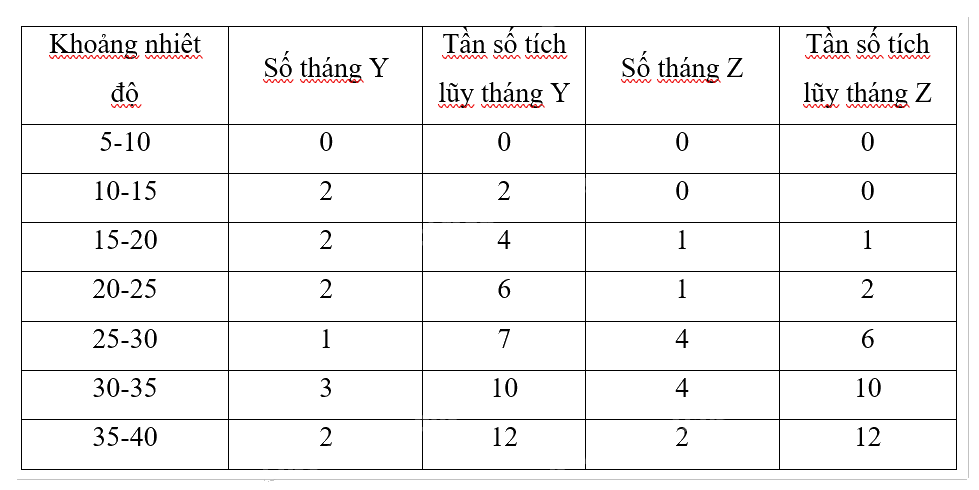
b) Tính khoảng tứ phân vị và so sánh
\(Q_1^Y = 15 + \frac{{3 - 2}}{2}.5 = 17,5;Q_3^Y = 30 + \frac{{9 - 7}}{3}.5 = 33,3\)
\(Q_1^Z = 25 + \frac{{3 - 2}}{4}.5 = 26,25;Q_3^Z = 30 + \frac{{9 - 6}}{4}.5 = 33,75\)
\(\begin{array}{l}\Delta _Q^Y = Q_3^Y - Q_1^Y = 33,3 - 17,5 = 15,8\\\Delta _Q^Z = Q_3^Z - Q_1^Z = 33,75 - 26,25 = 7,5\end{array}\)
Vì \(\Delta _Q^Y > \Delta _Q^Z\) nên nhiệt độ của địa phương Z ít biến động hơn.
- HĐ2
- LT3
- LT4
Trả lời câu hỏi Hoạt động 2 trang 89 SGK Toán 12 Cùng khám phá
Trở lại với bảng 3.1 về khối lượng của 100 quả dứa giống E. Để tiện tính toán, ta biểu diễn dữ liệu bằng một bảng hai cột như bảng trên.
a) Hãy tính các tứ phân vị của mẫu số liệu cho trong bảng.
b) Đề xuất một cách ước tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho.
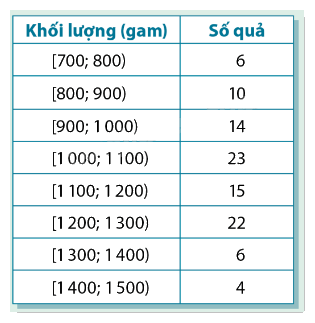
Phương pháp giải:
a) Sử dụng công thức tính tứ phân vị:
\({Q_x} = L + \left( {\frac{{{n_x} - F}}{f}} \right) \times h\)
Trong đó:
- \({Q_x}\) là giá trị tứ phân vị cần tìm \(\left( {{Q_1},{Q_2}} \right.\), hoặc \(\left. {{Q_3}} \right)\).
- \(L\) là cận dưới của khoảng chứa tứ phân vị.
- \({n_x}\) là vị trí của tứ phân vị trong tổng số mẫu (ví dụ, \({n_{{Q_1}}} = \frac{N}{4}\) cho \({\rm{Q}}1,{n_{{Q_2}}} = \frac{N}{2}\) cho Q2).
- \(F\) là tần suất tích lũy của khoảng liền trước khoảng chứa tứ phân vị.
- \(f\) là tần suất của khoảng chứa tứ phân vị.
- \(h\) là độ dài của khoảng giá trị (ví dụ: từ 900 đến 1000 thì \(h = 100\)).
b) Khoảng tứ phân vị là khoảng giữa \({Q_3}\) và \({Q_1}\), ký hiệu là: \({\Delta _Q} = {Q_3} - {Q_1}\).
Lời giải chi tiết:
a) Tính tần số tích luỹ
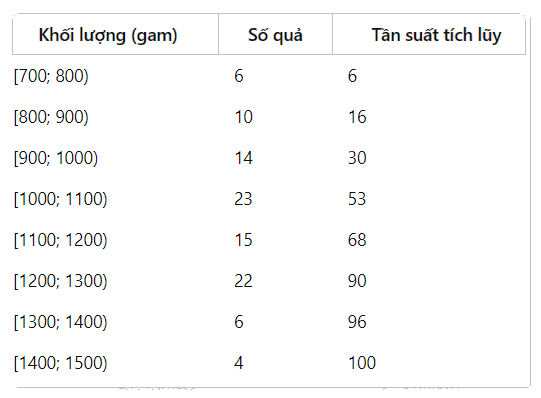
Kích thước của mẫu số liệu là \(N = 100\). Ta có \(\frac{N}{4} = 25;\frac{{2N}}{4} = 50;\frac{{3N}}{4} = 75\)
Nhóm chứa \({Q_1}\) là [900; 1000)
\({Q_1} = 900 + \frac{{25 - 16}}{{14}} \times 100 \approx 964,29{\rm{ gam}}\)
Nhóm chứa \({Q_2}\) là [1000; 1100)
\({Q_2} = 1000 + \frac{{50 - 30}}{{23}} \times 100 \approx 1086,96{\rm{ gam}}\)
Nhóm chứa \({Q_3}\) là [1200; 1300)
\({Q_3} = 1200 + \frac{{75 - 68}}{{22}} \times 100 \approx 1231,82{\rm{ gam}}\)
b) Khoảng tứ phân vị là: \({\Delta _Q} = {Q_3} - {Q_1} = 1231,82 - 964,29 = 267,53\)
Trả lời câu hỏi Luyện tập 3 trang 92 SGK Toán 12 Cùng khám phá
Ở một phòng điều trị nội trú của bệnh viện, dữ liệu thống kê thời gian ngủ hằng đêm của hai bệnh nhân trong suốt một tháng được tổng hợp bởi hai bảng dưới đây:
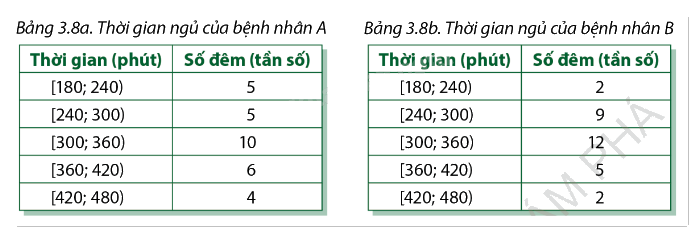
Bệnh nhân nào có thời gian ngủ ổn định hơn?
Phương pháp giải:
Tính tần suất tích lũy cho cả hai bệnh nhân.
Xác định \({Q_1}\), \({Q_2}\), và \({Q_3}\) cho mỗi bệnh nhân.
Tính khoảng tứ phân vị \({\Delta _Q}\) cho mỗi bệnh nhân.
So sánh khoảng tứ phân vị \({\Delta _Q}\) của hai bệnh nhân. Bệnh nhân có \({\Delta _Q}\) nhỏ hơn sẽ có thời gian ngủ ổn định hơn.
Lời giải chi tiết:
- Bệnh nhân A:
Tính tần suất tích luỹ:
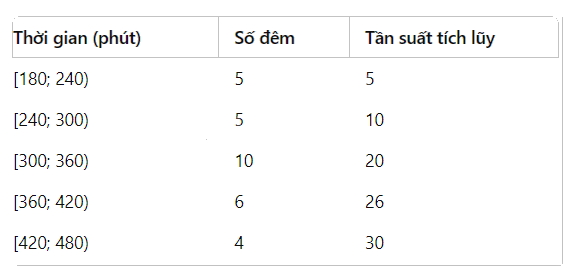
Tính tứ phân vị:
\({Q_1} = 240 + \frac{{7.5 - 5}}{5} \times 60 = 240 + 30 = 270\) phút
\({Q_2} = 300 + \frac{{15 - 10}}{{10}} \times 60 = 300 + 30 = 330\) phút
\({Q_3} = 360 + \frac{{22.5 - 20}}{6} \times 60 = 360 + 25 = 385\) phút
Khoảng tứ phân vị là:
\(\Delta _Q^A = {Q_3} - {Q_1} = 385 - 270 = 115\) phút
- Bệnh nhân B:
Tính tần suất tích luỹ:
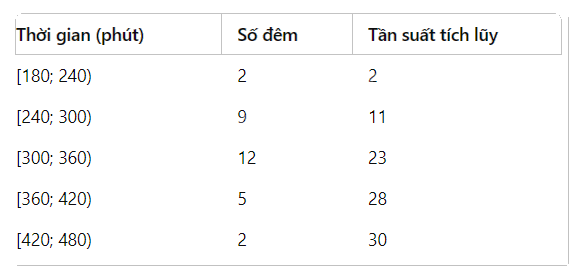
Tính tứ phân vị:
\({Q_1} = 240 + \frac{{7.5 - 2}}{9} \times 60 = 240 + 36,67 = 276,67\) phút
\({Q_2} = 300 + \frac{{15 - 11}}{{12}}.60 = 320\) phút
\({Q_3} = 300 + \frac{{22.5 - 11}}{{12}} \times 60 = 300 + 57,5 = 357,5\) phút
Khoảng tứ phân vị là:
\(\Delta _Q^B = {Q_3} - {Q_1} = 357.5 - 276.67 = 80.83\) phút
Vì \(\Delta _Q^B < \Delta _Q^A\) nên bệnh nhân B có thời gian ngủ ổn định hơn.
Trả lời câu hỏi Luyện tập 4 trang 93 SGK Toán 12 Cùng khám phá
Hình 3.3 là biểu đồ biểu diễn nhiệt độ trung bình hằng tháng của hai địa phương Y, Z.
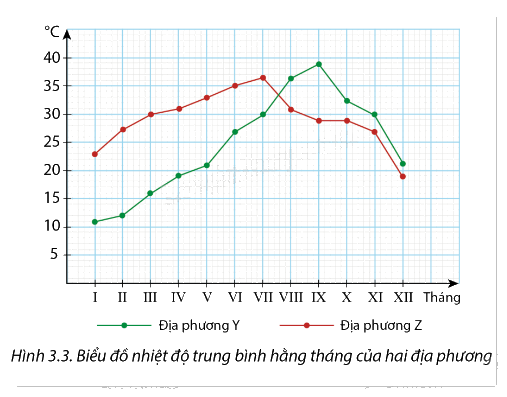
a) Lập bảng số liệu ghép nhóm về nhiệm độ của hai địa phương Y, Z, với độ dài các nhóm là 5 và đầu mút phải của nhóm cuối cùng là 40.
b) Tìm khoảng tứ phân vị của nhiệt độ mỗi địa phương và cho biết nhiệt độ của địa phương nào ít biến động hơn.
Phương pháp giải:
a)
- Tạo bảng với các hàng tương ứng với các khoảng nhiệt độ (5-10, 10-15, ..., 35-40) và hai cột tương ứng với địa phương Y và Z.
- Đếm số lượng tháng mà nhiệt độ trung bình rơi vào mỗi khoảng nhiệt độ cho từng địa phương.
b)
- Xác định khoảng tứ phân vị.
- Địa phương nào có khoảng tứ phân vị nhỏ hơn thì nhiệt độ của địa phương đó biến động ít hơn.
Lời giải chi tiết:
Đọc số liệu từ biểu đồ:
Lập bảng số liệu ghép nhóm:
b) Tính khoảng tứ phân vị và so sánh
\(Q_1^Y = 15 + \frac{{3 - 2}}{2}.5 = 17,5;Q_3^Y = 30 + \frac{{9 - 7}}{3}.5 = 33,3\)
\(Q_1^Z = 25 + \frac{{3 - 2}}{4}.5 = 26,25;Q_3^Z = 30 + \frac{{9 - 6}}{4}.5 = 33,75\)
\(\begin{array}{l}\Delta _Q^Y = Q_3^Y - Q_1^Y = 33,3 - 17,5 = 15,8\\\Delta _Q^Z = Q_3^Z - Q_1^Z = 33,75 - 26,25 = 7,5\end{array}\)
Vì \(\Delta _Q^Y > \Delta _Q^Z\) nên nhiệt độ của địa phương Z ít biến động hơn.
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 89 SGK Toán 12 Cùng khám phá
Trở lại với bảng 3.1 về khối lượng của 100 quả dứa giống E. Để tiện tính toán, ta biểu diễn dữ liệu bằng một bảng hai cột như bảng trên.
a) Hãy tính các tứ phân vị của mẫu số liệu cho trong bảng.
b) Đề xuất một cách ước tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho.
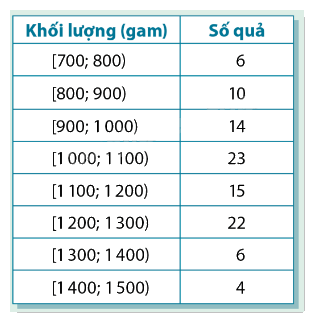
Phương pháp giải:
a) Sử dụng công thức tính tứ phân vị:
\({Q_x} = L + \left( {\frac{{{n_x} - F}}{f}} \right) \times h\)
Trong đó:
- \({Q_x}\) là giá trị tứ phân vị cần tìm \(\left( {{Q_1},{Q_2}} \right.\), hoặc \(\left. {{Q_3}} \right)\).
- \(L\) là cận dưới của khoảng chứa tứ phân vị.
- \({n_x}\) là vị trí của tứ phân vị trong tổng số mẫu (ví dụ, \({n_{{Q_1}}} = \frac{N}{4}\) cho \({\rm{Q}}1,{n_{{Q_2}}} = \frac{N}{2}\) cho Q2).
- \(F\) là tần suất tích lũy của khoảng liền trước khoảng chứa tứ phân vị.
- \(f\) là tần suất của khoảng chứa tứ phân vị.
- \(h\) là độ dài của khoảng giá trị (ví dụ: từ 900 đến 1000 thì \(h = 100\)).
b) Khoảng tứ phân vị là khoảng giữa \({Q_3}\) và \({Q_1}\), ký hiệu là: \({\Delta _Q} = {Q_3} - {Q_1}\).
Lời giải chi tiết:
a) Tính tần số tích luỹ
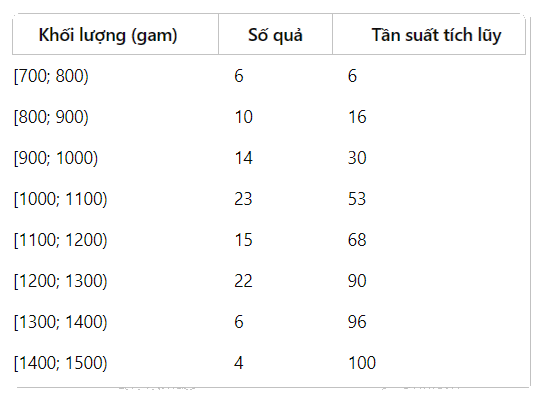
Kích thước của mẫu số liệu là \(N = 100\). Ta có \(\frac{N}{4} = 25;\frac{{2N}}{4} = 50;\frac{{3N}}{4} = 75\)
Nhóm chứa \({Q_1}\) là [900; 1000)
\({Q_1} = 900 + \frac{{25 - 16}}{{14}} \times 100 \approx 964,29{\rm{ gam}}\)
Nhóm chứa \({Q_2}\) là [1000; 1100)
\({Q_2} = 1000 + \frac{{50 - 30}}{{23}} \times 100 \approx 1086,96{\rm{ gam}}\)
Nhóm chứa \({Q_3}\) là [1200; 1300)
\({Q_3} = 1200 + \frac{{75 - 68}}{{22}} \times 100 \approx 1231,82{\rm{ gam}}\)
b) Khoảng tứ phân vị là: \({\Delta _Q} = {Q_3} - {Q_1} = 1231,82 - 964,29 = 267,53\)
Giải mục 2 trang 89, 90, 91, 92, 93 SGK Toán 12 tập 1 - Cùng khám phá
Mục 2 của SGK Toán 12 tập 1 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản và ứng dụng của đạo hàm trong việc giải các bài toán liên quan đến cực trị, tính đơn điệu của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng cho việc học tập các chương trình Toán học nâng cao hơn.
Nội dung chính của Mục 2 SGK Toán 12 tập 1
- Đạo hàm của hàm số: Định nghĩa đạo hàm, ý nghĩa hình học và vật lý của đạo hàm.
- Quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số.
- Đạo hàm của các hàm số cơ bản: Đạo hàm của hàm số lũy thừa, hàm số mũ, hàm số logarit, hàm số lượng giác và hàm số lượng giác ngược.
- Ứng dụng của đạo hàm: Giải các bài toán tìm cực trị, tính đơn điệu của hàm số, khảo sát hàm số.
Giải chi tiết các bài tập trang 89, 90, 91, 92, 93
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 2, trang 89, 90, 91, 92, 93 SGK Toán 12 tập 1:
Bài 1 (Trang 89)
Đề bài: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Lời giải:
f'(x) = 3x2 + 4x - 5
Bài 2 (Trang 90)
Đề bài: Tính đạo hàm của hàm số g(x) = sin(x) + cos(x).
Lời giải:
g'(x) = cos(x) - sin(x)
Bài 3 (Trang 91)
Đề bài: Tìm đạo hàm của hàm số h(x) = ex + ln(x).
Lời giải:
h'(x) = ex + 1/x
Bài 4 (Trang 92)
Đề bài: Cho hàm số y = x2 - 4x + 3. Tìm các điểm cực trị của hàm số.
Lời giải:
y' = 2x - 4. Giải phương trình y' = 0, ta được x = 2. Kiểm tra dấu của y' xung quanh x = 2, ta thấy y' đổi dấu từ âm sang dương, do đó hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là y(2) = -1.
Bài 5 (Trang 93)
Đề bài: Khảo sát hàm số y = x3 - 3x2 + 2x.
Lời giải:
y' = 3x2 - 6x + 2. Giải phương trình y' = 0, ta được x1 = (3 - √3)/3 và x2 = (3 + √3)/3. Khảo sát dấu của y' xung quanh các điểm này, ta xác định được các điểm cực trị và khoảng đồng biến, nghịch biến của hàm số.
Lưu ý khi giải bài tập về đạo hàm
- Nắm vững các quy tắc tính đạo hàm.
- Sử dụng đúng công thức đạo hàm của các hàm số cơ bản.
- Kiểm tra kỹ kết quả tính đạo hàm.
- Vận dụng đạo hàm để giải các bài toán liên quan đến cực trị, tính đơn điệu của hàm số.
Hy vọng với lời giải chi tiết này, các em sẽ hiểu rõ hơn về Mục 2 SGK Toán 12 tập 1 và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!