Giải bài 4.8 trang 8 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 4.8 trang 8 SBT Toán 12 - Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết bài 4.8 trang 8 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
Một viên đạn được bắn thẳng đứng lên trên từ mặt đất với vận tốc tại thời điểm t (t=0 là thời điểm viên đạn được bắn lên) cho bởi (vleft( t right) = 150 - 9,8t) (m/s). Tìm độ cao của viên đạn (tính từ mặt đất): a) Sau (t = 3) giây; b) Khi nó đạt độ cao lớn nhất (làm tròn kết quả đến chữ số thập phân thứ nhất của mét).
Đề bài
Một viên đạn được bắn thẳng đứng lên trên từ mặt đất với vận tốc tại thời điểm t (t=0 là thời điểm viên đạn được bắn lên) cho bởi \(v\left( t \right) = 150 - 9,8t\) (m/s).
Tìm độ cao của viên đạn (tính từ mặt đất):
a) Sau \(t = 3\) giây;
b) Khi nó đạt độ cao lớn nhất (làm tròn kết quả đến chữ số thập phân thứ nhất của mét).
Phương pháp giải - Xem chi tiết
Ý a: Độ cao \(h\left( t \right)\) của viên đạn tại thời điểm \(t\) là một nguyên hàm của hàm vận tốc \(v\left( t \right)\).
Tìm \(h\left( t \right)\) sau đó tính \(h\left( 3 \right)\).
Ý b: Tìm giá trị lớn nhất của \(h\left( t \right)\) với \(t \ge 0\). Lập bảng biến thiên để tìm.
Lời giải chi tiết
a) Độ cao \(h\left( t \right)\) của viên đạn tại thời điểm \(t\) là một nguyên hàm của hàm vận tốc \(v\left( t \right)\).
Ta có \(h\left( t \right) = \int {\left( {150 - 9,8t} \right)} dt = 150t - 4,9{t^2} + C\).
Do \(t = 0\) là thời điểm viên đạn được bắn lên nên \(h\left( 0 \right) = 0\).
Suy ra \(150 \cdot 0 - 4,9 \cdot {0^2} + C = 0 \Leftrightarrow C = 0 \Leftrightarrow \)\(h\left( t \right) = 150t - 4,9{t^2}\).
Độ cao của viên đạn sau 3 giây là \(h\left( 3 \right) = 150 \cdot 3 - 4,9 \cdot {3^2} = 405,9\) (m).
b) Độ cao lớn nhất của viên đạn là giá trị lớn nhất của hàm số \(h\left( t \right) = 150t - 4,9{t^2}\) với \(t \ge 0\).
Ta có \(h'\left( t \right) = 150 - 9,8t\) suy ra \(h'\left( t \right) = 0 \Leftrightarrow 150 - 9,8t = 0 \Leftrightarrow t = \frac{{750}}{{49}}\).
Ta lập bảng biến thiên
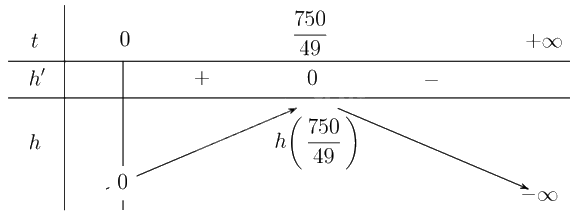
Từ bảng biến thiên suy ra \(\mathop {\max }\limits_{\left[ {0; + \infty } \right)} h\left( t \right) = h\left( {\frac{{750}}{{49}}} \right) = \frac{{56250}}{{49}} \approx 1147,96\).
Vậy viên đạt đạt độ cao lớn nhất khoảng \(1147,96\) m tại thời điểm \(t = \frac{{750}}{{49}}\) giây.
Giải bài 4.8 trang 8 SBT Toán 12 - Kết nối tri thức: Tổng quan
Bài 4.8 trang 8 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tính đạo hàm, tìm cực trị, hoặc khảo sát hàm số. Việc nắm vững các công thức đạo hàm cơ bản và kỹ năng biến đổi đại số là rất quan trọng để giải quyết bài toán này một cách hiệu quả.
Nội dung bài 4.8 trang 8 SBT Toán 12 - Kết nối tri thức
Bài 4.8 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của một hàm số cho trước, có thể là hàm số đơn giản hoặc hàm số phức tạp.
- Tìm đạo hàm cấp hai: Yêu cầu tìm đạo hàm cấp hai của một hàm số.
- Ứng dụng đạo hàm để giải quyết các bài toán thực tế: Ví dụ như tìm vận tốc, gia tốc, hoặc tối ưu hóa một đại lượng nào đó.
Lời giải chi tiết bài 4.8 trang 8 SBT Toán 12 - Kết nối tri thức
Để giúp bạn hiểu rõ hơn về cách giải bài 4.8 trang 8 SBT Toán 12 Kết nối tri thức, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. (Ở đây sẽ là lời giải chi tiết của bài 4.8, ví dụ:)
Ví dụ: Giả sử bài 4.8 yêu cầu tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Lời giải:
f'(x) = 3x2 + 4x - 5
Các lưu ý khi giải bài 4.8 trang 8 SBT Toán 12 - Kết nối tri thức
- Nắm vững các công thức đạo hàm cơ bản: Đạo hàm của xn, sin(x), cos(x), ex, ln(x),...
- Sử dụng quy tắc đạo hàm: Quy tắc tích, quy tắc thương, quy tắc chuỗi,...
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả đạo hàm của bạn là chính xác.
- Luyện tập thường xuyên: Giải nhiều bài tập tương tự để nâng cao kỹ năng giải toán.
Tài liệu tham khảo hữu ích
Để hỗ trợ bạn trong quá trình học tập và giải bài tập, chúng tôi xin giới thiệu một số tài liệu tham khảo hữu ích:
- Sách giáo khoa Toán 12 - Kết nối tri thức
- Sách bài tập Toán 12 - Kết nối tri thức
- Các trang web học Toán trực tuyến uy tín
Kết luận
Hy vọng rằng với lời giải chi tiết và những lưu ý trên, bạn đã có thể tự tin giải bài 4.8 trang 8 SBT Toán 12 Kết nối tri thức. Đừng ngần ngại liên hệ với Tusach.vn nếu bạn có bất kỳ câu hỏi nào. Chúc bạn học tập tốt!