Giải bài 1.67 trang 36 Sách bài tập Toán 12 - Kết nối tri thức

Giải bài 1.67 trang 36 sách bài tập toán 12 - Kết nối tri thức

Giải bài 1.67 trang 36 SBT Toán 12 Kết nối tri thức

Chào mừng bạn đến với lời giải chi tiết bài 1.67 trang 36 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Chúng tôi luôn cố gắng cung cấp những lời giải chính xác và đầy đủ nhất, đồng thời giải thích rõ ràng từng bước để bạn có thể hiểu sâu sắc bản chất của vấn đề.

Cắt bỏ hình quạt tròn OAB (hình phẳng có nét gạch trong hình dưới đây) từ một mảnh các tông hình tròn bán kính R rồi dán hai bán kính OA và OB của hình quạt tròn còn lại với nhau được một cái phễu có dạng của một hình nón. Gọi x là góc ở tâm của quạt tròn dùng làm phễu (left( {0 < x < 2pi } right)). a) Hãy biểu diễn bán kính đáy r và đường cao h của hình nón theo R và x. b) Tính thể tích của hình nón theo R và x c) Tìm x để hình nón có thể tích lớn nhất và tính giá trị lớn nhất đó.

Đề bài

Cắt bỏ hình quạt tròn OAB (hình phẳng có nét gạch trong hình dưới đây) từ một mảnh các tông hình tròn bán kính R rồi dán hai bán kính OA và OB của hình quạt tròn còn lại với nhau được một cái phễu có dạng của một hình nón. Gọi x là góc ở tâm của quạt tròn dùng làm phễu \(\left( {0 < x < 2\pi } \right)\).

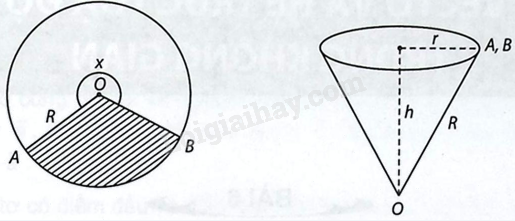
Giải bài 1.67 trang 36 sách bài tập toán 12 - Kết nối tri thức 1

a) Hãy biểu diễn bán kính đáy r và đường cao h của hình nón theo R và x.

b) Tính thể tích của hình nón theo R và x

c) Tìm x để hình nón có thể tích lớn nhất và tính giá trị lớn nhất đó.

Phương pháp giải - Xem chi tiết Giải bài 1.67 trang 36 sách bài tập toán 12 - Kết nối tri thức 2

Ý a: Chu vi đáy hình nón bằng độ dài cung AB, từ đó tìm được r, áp dụng định lý Pythagore để tìm h.

Ý b: Sau khi đã biết bán kính và chiều cao từ ý a, áp dụng công thức tính thể tích hình nón để tìm được V.

Ý c: Xét hàm số V theo x để tìm giá trị lớn nhất của hàm số trên \(\left( {0;2\pi } \right)\).

Lời giải chi tiết

a) Vì độ dài của đường tròn đáy hình nón (chu vi đáy) bằng độ dài của quạt tròn dùng làm phễu nên ta có \(2\pi r = Rx \Leftrightarrow r = \frac{{Rx}}{{2\pi }}\). Khi đó ta có:

\(h = \sqrt {{R^2} - {r^2}} = \sqrt {{R^2} - \frac{{{R^2}{x^2}}}{{4{\pi ^2}}}} = \frac{R}{{2\pi }}\sqrt {4{\pi ^2} - {x^2}} \).

b) Thể tích hình nón là \(V = \frac{1}{3}\pi {r^2}h = \frac{{{R^3}}}{{24{\pi ^2}}}{x^2}\sqrt {4{\pi ^2} - {x^2}} \).

c) Ta cần tìm \(x \in \left( {0;2\pi } \right)\) để thể tích \(V\) đạt giá trị lớn nhất.

Xét hàm số \(V = \frac{{{R^3}}}{{24{\pi ^2}}}{x^2}\sqrt {4{\pi ^2} - {x^2}} ,x \in \left( {0;2\pi } \right)\).

Ta có \(V' = \frac{{{R^3}}}{{24{\pi ^2}}}\frac{{x\left( {8{\pi ^2} - 3{x^2}} \right)}}{{\sqrt {4{\pi ^2} - {x^2}} }}\) suy ra \(V' = 0 \Leftrightarrow x\left( {8{\pi ^2} - 3{x^2}} \right) = 0 \Leftrightarrow x = \frac{{2\sqrt 6 }}{3}\pi \), do \(x > 0\).

Lập bảng biến thiên:

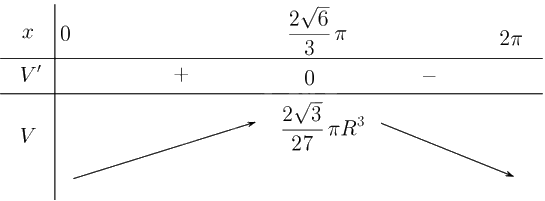
Giải bài 1.67 trang 36 sách bài tập toán 12 - Kết nối tri thức 3

Hình nón có diện tích lớn nhất khi \(x = \frac{{2\sqrt 6 }}{3}\pi \) khi đó \(\mathop {\max }\limits_{\left( {0;2\pi } \right)} V = V\left( {\frac{{2\sqrt 6 }}{3}\pi } \right) = \frac{{2\sqrt 3 }}{{27}}\pi {R^3}\).

Giải bài 1.67 trang 36 SBT Toán 12 Kết nối tri thức: Chi tiết và Dễ hiểu

Bài 1.67 trang 36 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này thường liên quan đến việc ứng dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế, đặc biệt là trong lĩnh vực kinh tế và kỹ thuật.

Nội dung bài tập 1.67 trang 36 SBT Toán 12 Kết nối tri thức

Thông thường, bài tập 1.67 yêu cầu học sinh:

Xác định hàm số biểu diễn một đại lượng nào đó (ví dụ: chi phí sản xuất, doanh thu, lợi nhuận).
Tính đạo hàm của hàm số đó.
Tìm điểm cực trị của hàm số.
Giải thích ý nghĩa của điểm cực trị trong bối cảnh bài toán.

Phương pháp giải bài tập 1.67 trang 36 SBT Toán 12 Kết nối tri thức

Để giải bài tập này một cách hiệu quả, bạn cần:

Nắm vững kiến thức về đạo hàm: Hiểu rõ các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản, và ứng dụng của đạo hàm trong việc tìm cực trị.
Đọc kỹ đề bài: Xác định rõ các thông tin đã cho và yêu cầu của bài toán.
Xây dựng mô hình toán học: Biểu diễn bài toán bằng các biểu thức toán học, bao gồm hàm số và các điều kiện ràng buộc.
Giải phương trình: Sử dụng các phương pháp giải phương trình để tìm ra các giá trị cần thiết.
Kiểm tra kết quả: Đảm bảo rằng kết quả tìm được phù hợp với bối cảnh bài toán và có ý nghĩa thực tế.

Ví dụ minh họa giải bài 1.67 trang 36 SBT Toán 12 Kết nối tri thức

Đề bài: Một công ty sản xuất x sản phẩm với chi phí sản xuất là C(x) = 2x² + 10x + 100 (đơn vị: triệu đồng). Giá bán mỗi sản phẩm là 50 triệu đồng. Hãy xác định số lượng sản phẩm cần sản xuất để đạt lợi nhuận tối đa.

Lời giải:

1. Hàm doanh thu: R(x) = 50x (triệu đồng)

2. Hàm lợi nhuận: P(x) = R(x) - C(x) = 50x - (2x² + 10x + 100) = -2x² + 40x - 100 (triệu đồng)

3. Tính đạo hàm của hàm lợi nhuận: P'(x) = -4x + 40

4. Tìm điểm cực trị: P'(x) = 0 => -4x + 40 = 0 => x = 10

5. Kiểm tra điều kiện cực đại: P''(x) = -4 < 0 => x = 10 là điểm cực đại

Kết luận: Để đạt lợi nhuận tối đa, công ty cần sản xuất 10 sản phẩm.

Lưu ý khi giải bài tập 1.67 trang 36 SBT Toán 12 Kết nối tri thức

Hãy chú ý đến đơn vị của các đại lượng trong bài toán. Đảm bảo rằng bạn sử dụng đúng đơn vị khi tính toán và diễn giải kết quả. Ngoài ra, hãy kiểm tra kỹ các điều kiện ràng buộc của bài toán để đảm bảo rằng kết quả tìm được là hợp lý.

Tài liệu tham khảo hữu ích

Sách giáo khoa Toán 12 Kết nối tri thức
Sách bài tập Toán 12 Kết nối tri thức
Các trang web học Toán trực tuyến uy tín

Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 1.67 trang 36 SBT Toán 12 Kết nối tri thức một cách hiệu quả. Chúc bạn học tập tốt!