Giải bài 2.32 trang 55 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 2.32 trang 55 SBT Toán 12 - Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết bài 2.32 trang 55 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
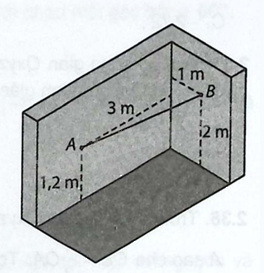
Hình bên mô tả hai bức tường gạch được xây vuông góc với nhau và cùng vuông góc với mặt đất. Một người thợ xây căng dây giữa hai bức tường. Đầu A của sợi dây nằm trên bức tường thứ nhất, cách bức tường thứ 2 là 3 m và cách mặt đất là 1,2 m. Đầu B của sợi dây nằm trên bức tường thứ 2, cách bức tường thứ nhất là 1 m và cách mặt đất là 2 m. a) Hãy lập một hệ trục tọa độ phù hợp và tìm tọa độ của hai đầu (A,B) trong hệ tọa độ đó. b) Tính độ dài của sợi dây được căng.
Đề bài
Hình bên mô tả hai bức tường gạch được xây vuông góc với nhau và cùng vuông góc với mặt đất. Một người thợ xây căng dây giữa hai bức tường. Đầu A của sợi dây nằm trên bức tường thứ nhất, cách bức tường thứ 2 là 3 m và cách mặt đất là 1,2 m. Đầu B của sợi dây nằm trên bức tường thứ 2, cách bức tường thứ nhất là 1 m và cách mặt đất là 2 m.
a) Hãy lập một hệ trục tọa độ phù hợp và tìm tọa độ của hai đầu \(A,B\) trong hệ tọa độ đó.
b) Tính độ dài của sợi dây được căng.
Phương pháp giải - Xem chi tiết
Ý a: Theo mối quan hệ vuông góc giữa ba mặt (đôi một vuông góc) gồm hai bức tường và mặt đất ta lập được hệ trục tọa độ. Sau khi lập, quan sát hình vẽ ta xác định được tọa độ các điểm A, B.
Ý b: Độ dài sợi dây là độ dài đoạn AB, áp dụng công thức khoảng cách giữa hai điểm để tính.
Lời giải chi tiết
a) Chọn hệ trục tọa độ như hình vẽ, trong đó \(O\) là góc tường, giao của hai mặt bên là tia \(Oz\), giao của mặt bên và đáy lần lượt là hai tia \(Ox,{\rm{ }}Oy\). Khi đó \(A\left( {3;0;1,2} \right)\) và \(B\left( {0;1;2} \right)\).
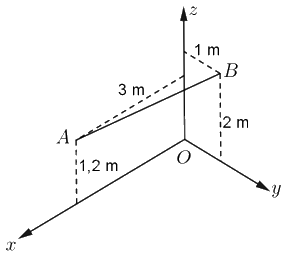
b) Độ dài của sợi dây được căng là \(AB = \sqrt {9 + 1 + {{0,8}^2}} = \frac{{\sqrt {266} }}{5} \approx 3,26\) m.
Giải bài 2.32 trang 55 SBT Toán 12 - Kết nối tri thức: Tổng quan
Bài 2.32 trang 55 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tính đơn điệu, cực trị của hàm số, hoặc các bài toán ứng dụng thực tế.
Nội dung bài 2.32 trang 55 SBT Toán 12 - Kết nối tri thức
Để giải quyết bài 2.32 trang 55 SBT Toán 12 - Kết nối tri thức, bạn cần:
- Xác định đúng yêu cầu của bài toán: Đọc kỹ đề bài để hiểu rõ cần tìm gì (ví dụ: tìm đạo hàm, tìm cực trị, khảo sát hàm số,...).
- Vận dụng các công thức đạo hàm: Sử dụng các công thức đạo hàm cơ bản và quy tắc đạo hàm để tính đạo hàm của hàm số.
- Phân tích và giải quyết bài toán: Dựa vào đạo hàm để xác định tính đơn điệu, cực trị của hàm số, hoặc giải quyết các bài toán ứng dụng.
- Kiểm tra lại kết quả: Đảm bảo kết quả của bạn là chính xác và phù hợp với yêu cầu của bài toán.
Lời giải chi tiết bài 2.32 trang 55 SBT Toán 12 - Kết nối tri thức
(Giả sử bài toán cụ thể là: Tìm đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1)
Lời giải:
Để tìm đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1, ta sử dụng quy tắc đạo hàm của tổng và hiệu, cũng như quy tắc đạo hàm của lũy thừa:
f'(x) = (x3)' - (3x2)' + (2x)' - (1)'
f'(x) = 3x2 - 6x + 2 - 0
f'(x) = 3x2 - 6x + 2
Vậy, đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1 là f'(x) = 3x2 - 6x + 2.
Các dạng bài tập tương tự và phương pháp giải
Ngoài bài 2.32, sách bài tập Toán 12 Kết nối tri thức còn nhiều bài tập tương tự về đạo hàm. Để giải quyết các bài tập này, bạn có thể áp dụng các phương pháp sau:
- Sử dụng bảng đạo hàm cơ bản: Nắm vững bảng đạo hàm cơ bản để tính đạo hàm của các hàm số đơn giản.
- Vận dụng quy tắc đạo hàm: Sử dụng các quy tắc đạo hàm (quy tắc tổng, hiệu, tích, thương, hàm hợp) để tính đạo hàm của các hàm số phức tạp.
- Giải phương trình đạo hàm: Giải phương trình đạo hàm để tìm các điểm cực trị của hàm số.
- Khảo sát hàm số: Sử dụng đạo hàm để khảo sát tính đơn điệu, cực trị, điểm uốn của hàm số.
Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là một website cung cấp đầy đủ các tài liệu học tập Toán 12, bao gồm sách giáo khoa, sách bài tập, đề thi, lời giải chi tiết và các bài viết hướng dẫn giải bài tập. Chúng tôi cam kết cung cấp cho bạn những thông tin chính xác, hữu ích và dễ hiểu nhất. Hãy truy cập tusach.vn để đồng hành cùng bạn trên con đường chinh phục môn Toán!
Bảng tổng hợp các công thức đạo hàm cơ bản
| Hàm số y = f(x) | Đạo hàm y' = f'(x) |
|---|---|
| C (hằng số) | 0 |
| xn | nxn-1 |
| sin x | cos x |
| cos x | -sin x |