Giải bài 4.39 trang 20 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 4.39 trang 20 SBT Toán 12 - Kết nối tri thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài 4.39 trang 20 một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho (S) là diện tích phần hình phẳng được tô màu như Hình 4.7. Khi đó diện tích (S) là A. (S = intlimits_a^b {left| {fleft( x right) - gleft( x right)} right|dx} ). B. (S = intlimits_a^m {left| {fleft( x right) - gleft( x right)} right|dx} + intlimits_m^b {left| {gleft( x right) - fleft( x right)} right|dx} ). C. (S = intlimits_a^m {left| {fleft( x right)} right|dx} + intlimits_m^b {left| {gleft( x right)} right|dx} ). D. (S = i
Đề bài
Cho \(S\) là diện tích phần hình phẳng được tô màu như Hình 4.7.
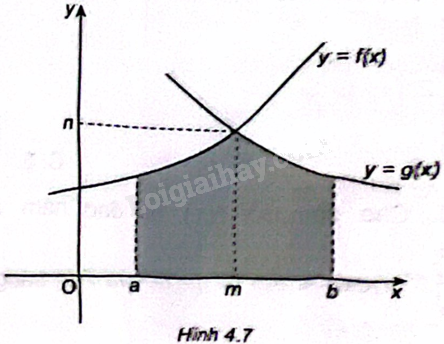
Khi đó diện tích \(S\) là
A. \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
B. \(S = \int\limits_a^m {\left| {f\left( x \right) - g\left( x \right)} \right|dx} + \int\limits_m^b {\left| {g\left( x \right) - f\left( x \right)} \right|dx} \).
C. \(S = \int\limits_a^m {\left| {f\left( x \right)} \right|dx} + \int\limits_m^b {\left| {g\left( x \right)} \right|dx} \).
D. \(S = \int\limits_a^m {\left| {g\left( x \right)} \right|dx} + \int\limits_m^b {\left| {f\left( x \right)} \right|dx} \).
Phương pháp giải - Xem chi tiết
Xét hình phẳng đang cần tìm diện tích, ta chia hình thành hai hình nhỏ và tính diện tích từng hình. \({S_1}\) là diện tích hình phẳng được giới hạn bởi đồ thị \(y = f\left( x \right)\), trục \(Ox\), đường thẳng \(x = a,x = m\) và \({S_2}\) là diện tích hình phẳng được giới hạn bởi đồ thị \(y = g\left( x \right)\), trục \(Ox\), đường thẳng \(x = m,x = b\). Áp dụng công thức tính diện tích ứng dụng tích phân đã học.
Lời giải chi tiết
Từ hình vẽ ta thấy \(S = {S_1} + {S_2}\), trong đó \({S_1}\) là diện tích hình phẳng được giới hạn bởi đồ thị \(y = f\left( x \right)\), trục \(Ox\), đường thẳng \(x = a,x = m\) và \({S_2}\) là diện tích hình phẳng được giới hạn bởi đồ thị \(y = g\left( x \right)\), trục \(Ox\), đường thẳng \(x = m,x = b\).
Ta có \({S_1} = \int\limits_a^m {\left| {f\left( x \right)} \right|dx} \) và \({S_2} = \int\limits_m^b {\left| {g\left( x \right)} \right|dx} \) suy ra \(S = \int\limits_a^m {\left| {f\left( x \right)} \right|dx} + \int\limits_m^b {\left| {g\left( x \right)} \right|dx} \).
Chọn C
Giải bài 4.39 trang 20 SBT Toán 12 - Kết nối tri thức: Hướng dẫn chi tiết
Bài 4.39 trang 20 sách bài tập Toán 12 Kết nối tri thức yêu cầu chúng ta giải một bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
- Đạo hàm của hàm số: Cách tính đạo hàm của các hàm số cơ bản và các hàm số phức tạp.
- Điều kiện cần và đủ để hàm số đạt cực trị: Các bước tìm cực trị của hàm số.
- Ứng dụng của đạo hàm trong việc khảo sát hàm số: Xác định khoảng đồng biến, nghịch biến, cực trị, và điểm uốn của hàm số.
Nội dung bài 4.39: (Giả sử bài toán cụ thể là tìm cực trị của hàm số f(x) = x^3 - 3x^2 + 2)
Lời giải:
- Tính đạo hàm cấp một: f'(x) = 3x^2 - 6x
- Tìm điểm dừng: Giải phương trình f'(x) = 0, ta được x = 0 hoặc x = 2.
- Tính đạo hàm cấp hai: f''(x) = 6x - 6
- Xác định cực trị:
- Tại x = 0: f''(0) = -6 < 0 => Hàm số đạt cực đại tại x = 0. Giá trị cực đại là f(0) = 2.
- Tại x = 2: f''(2) = 6 > 0 => Hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là f(2) = -2.
- Kết luận: Hàm số f(x) = x^3 - 3x^2 + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Lưu ý:
Khi giải các bài toán về đạo hàm, bạn cần chú ý đến các bước sau:
- Xác định đúng hàm số cần khảo sát.
- Tính đạo hàm một cách chính xác.
- Tìm đúng các điểm dừng và điểm không xác định.
- Sử dụng đạo hàm cấp hai để xác định loại cực trị.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Các bài tập tương tự:
Để luyện tập thêm, bạn có thể tham khảo các bài tập sau trong sách bài tập Toán 12 Kết nối tri thức:
- Bài 4.40 trang 20
- Bài 4.41 trang 21
- Bài 4.42 trang 21
Tusach.vn hy vọng rằng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về cách giải bài 4.39 trang 20 sách bài tập Toán 12 Kết nối tri thức. Chúc bạn học tập tốt!
Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi. Chúng tôi luôn sẵn sàng hỗ trợ bạn.
| Bài tập | Lời giải |
|---|---|
| 4.39 trang 20 | Xem chi tiết ở trên |