Giải bài 1.1 trang 8 SBT Toán 12 - Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết bài 1.1 trang 8 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
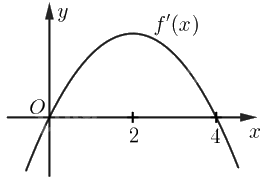
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và đạo hàm \(f'\left( x \right)\) có đồ thị như hình bên. Sử dụng đồ thị của hàm số \(y = f'\left( x \right)\), hãy cho biết:
a) Các khoảng đồng biến, khoảng nghịch biến của hàm số \(f\left( x \right)\);
b) Hàm số \(f\left( x \right)\) có cực đại, cực tiểu không? Nếu có, hãy cho biết các điểm cực trị tương ứng.
Giải bài 1.1 trang 8 SBT Toán 12 - Kết nối tri thức: Tổng quan và Phương pháp
Bài 1.1 trang 8 sách bài tập Toán 12 Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này thường tập trung vào việc kiểm tra kiến thức cơ bản về tập xác định của hàm số, các phép toán trên tập hợp và cách biểu diễn hàm số.
Nội dung bài tập 1.1 trang 8 SBT Toán 12 - Kết nối tri thức
Bài tập 1.1 thường yêu cầu:
- Xác định tập xác định của hàm số.
- Tìm điều kiện để hàm số có nghĩa.
- Thực hiện các phép toán trên tập hợp (hợp, giao, hiệu, bù).
- Biểu diễn hàm số bằng công thức hoặc đồ thị.
Lời giải chi tiết bài 1.1 trang 8 SBT Toán 12 - Kết nối tri thức
Để giải bài 1.1 trang 8 SBT Toán 12 Kết nối tri thức một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Tập xác định của hàm số: Tập xác định của hàm số y = f(x) là tập hợp tất cả các giá trị x sao cho f(x) có nghĩa.
- Điều kiện để hàm số có nghĩa: Ví dụ, với hàm số y = √(x-a), điều kiện để hàm số có nghĩa là x - a ≥ 0.
- Các phép toán trên tập hợp: Nắm vững các quy tắc hợp, giao, hiệu, bù của các tập hợp.
Ví dụ minh họa:
Giả sử bài tập yêu cầu tìm tập xác định của hàm số y = 1/(x-2).
Lời giải:
Hàm số y = 1/(x-2) có nghĩa khi và chỉ khi mẫu số khác 0, tức là x - 2 ≠ 0. Do đó, x ≠ 2. Vậy tập xác định của hàm số là D = R \ {2}.
Mẹo giải nhanh và hiệu quả
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài tập.
- Xác định các điều kiện để hàm số có nghĩa.
- Sử dụng các công thức và quy tắc toán học một cách chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
Bài tập tương tự và luyện tập
Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 12 Kết nối tri thức hoặc trên các trang web học toán trực tuyến.
Bảng tổng hợp các dạng bài tập thường gặp
| Dạng bài tập | Ví dụ |
|---|
| Tìm tập xác định | y = √(x+1) |
| Thực hiện phép toán trên tập hợp | A = {1, 2, 3}, B = {2, 4, 5}. Tìm A ∪ B |
Kết luận:
Bài 1.1 trang 8 SBT Toán 12 Kết nối tri thức là một bài tập cơ bản nhưng quan trọng. Việc nắm vững kiến thức và phương pháp giải bài tập này sẽ giúp bạn tự tin hơn trong quá trình học tập môn Toán.
Chúc bạn học tốt!
