Giải bài 1.42 trang 31 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 1.42 trang 31 SBT Toán 12 - Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết bài 1.42 trang 31 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác và đầy đủ nhất, đồng thời giải thích rõ ràng từng bước để bạn có thể hiểu sâu sắc bản chất của vấn đề.
Doanh số bán hệ thống âm thanh nổi mới trong khoảng thời gian dự kiến sẽ tuân theo đường cong logistic \(R = R\left( x \right) = \frac{{5000}}{{1 + 5{e^{ - x}}}},x \ge 0\), trong đó thời gian \(x\) được tính bằng năm. Hỏi tốc độ bán hàng đạt tối đa vào năm nào?
Đề bài
Doanh số bán hệ thống âm thanh nổi mới trong khoảng thời gian dự kiến sẽ tuân theo đường cong logistic \(R = R\left( x \right) = \frac{{5000}}{{1 + 5{e^{ - x}}}},x \ge 0\), trong đó thời gian \(x\) được tính bằng năm. Hỏi tốc độ bán hàng đạt tối đa vào năm nào?
Phương pháp giải - Xem chi tiết
+ Tìm công thức \(R'\left( x \right)\).
+ Tìm \(x\) để \(R'\left( x \right)\) đạt giá trị lớn nhất.
Lời giải chi tiết
Hàm biểu thị tốc độ bán hàng là \(R'\left( x \right) = \frac{{25000{e^{ - x}}}}{{{{\left( {1 + 5{e^{ - x}}} \right)}^2}}},{\rm{ x}} \ge 0\).
Tốc độ bán hàng tối đa khi \(R'\left( x \right)\) đạt giá trị lớn nhất, ta cần tìm giá trị lớn nhất của \(R'\left( x \right)\) trên \(\left[ {0; + \infty } \right)\).
Ta có \(R''\left( x \right) = - 25000 \cdot \frac{{{e^{ - x}}{{\left( {1 + 5{e^{ - x}}} \right)}^2} + {e^{ - x}} \cdot 2\left( {1 + 5{e^{ - x}}} \right) \cdot 5{e^{ - x}}}}{{{{\left( {1 + 5{e^{ - x}}} \right)}^4}}} = \frac{{25000\left( {5{e^{ - x}} - 1} \right)}}{{{{\left( {1 + 5{e^{ - x}}} \right)}^3}}}\)
Khi đó \(R''\left( x \right) = 0 \Leftrightarrow \frac{{25000\left( {5{e^{ - x}} - 1} \right)}}{{{{\left( {1 + 5{e^{ - x}}} \right)}^3}}} = 0 \Leftrightarrow \left( {5{e^{ - x}} - 1} \right) = 0 \Leftrightarrow x = \ln 5\).
Lập bảng biến thiên
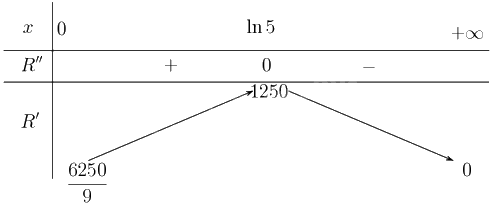
Từ bảng biến thiên suy ra \(R'\) đạt giá trị lớn nhất tại \(x = \ln 5 \approx 1,61\). Vậy tốc độ bán hàng đạt tối đa vào thời điểm năm thứ hai.
Giải bài 1.42 trang 31 SBT Toán 12 - Kết nối tri thức: Phân tích và Lời giải Chi Tiết
Bài 1.42 trang 31 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng, thường xuất hiện trong các đề thi và kiểm tra. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Để giúp các bạn học sinh hiểu rõ hơn về bài tập này, tusach.vn xin trình bày lời giải chi tiết như sau:
Đề bài:
(Nội dung đề bài bài 1.42 trang 31 SBT Toán 12 - Kết nối tri thức sẽ được chèn vào đây. Ví dụ: Cho hàm số y = f(x) có đạo hàm f'(x) = 3x2 - 6x + 1. Tìm các điểm cực trị của hàm số.)
Lời giải:
Để tìm các điểm cực trị của hàm số, ta cần thực hiện các bước sau:
- Bước 1: Tìm tập xác định của hàm số.
- Bước 2: Tính đạo hàm cấp một f'(x). (Đã cho trong đề bài)
- Bước 3: Giải phương trình f'(x) = 0 để tìm các điểm nghi ngờ là cực trị.
- Bước 4: Xét dấu đạo hàm f'(x) để xác định loại cực trị.
Chi tiết lời giải:
(Giải chi tiết từng bước, kèm theo giải thích rõ ràng. Ví dụ: Giải phương trình 3x2 - 6x + 1 = 0, ta được x1 = (3 + √6)/3 và x2 = (3 - √6)/3. Xét dấu đạo hàm f'(x) trên các khoảng (-∞; (3 - √6)/3), ((3 - √6)/3; (3 + √6)/3), và ((3 + √6)/3; +∞), ta thấy f'(x) đổi dấu từ dương sang âm tại x1, do đó x1 là điểm cực đại. Tương tự, f'(x) đổi dấu từ âm sang dương tại x2, do đó x2 là điểm cực tiểu.)
Kết luận:
Hàm số y = f(x) đạt cực đại tại x = (3 + √6)/3 và đạt cực tiểu tại x = (3 - √6)/3.
Lưu ý quan trọng:
- Luôn kiểm tra tập xác định của hàm số trước khi tính đạo hàm.
- Khi xét dấu đạo hàm, cần xác định đúng các khoảng và dấu của đạo hàm trên mỗi khoảng.
- Nắm vững các quy tắc tính đạo hàm để tránh sai sót.
Các bài tập tương tự:
Để luyện tập thêm, bạn có thể tham khảo các bài tập tương tự trong sách bài tập Toán 12 Kết nối tri thức, hoặc tìm kiếm trên tusach.vn với các từ khóa như:
- Giải bài 1.43 trang 31 SBT Toán 12
- Bài tập về đạo hàm Toán 12
- Các dạng bài tập cực trị Toán 12
Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục Toán học!
Tusach.vn hy vọng rằng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về bài 1.42 trang 31 sách bài tập Toán 12 Kết nối tri thức. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.
| Chủ đề | Nội dung |
|---|---|
| Mục tiêu bài học | Vận dụng kiến thức về đạo hàm để tìm cực trị của hàm số. |
| Phương pháp giải | Tìm đạo hàm cấp một, giải phương trình đạo hàm bằng 0, xét dấu đạo hàm. |
| Tài liệu tham khảo | Sách bài tập Toán 12 Kết nối tri thức, tusach.vn |