Giải bài 1.19 trang 16 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 1.19 trang 16 SBT Toán 12 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 1.19 trang 16 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu nhất.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Một vật được phóng lên trời theo một góc xiên (theta left( {{{45}^ circ } < theta < {{90}^ circ }} right)) so với phương ngang với vận tốc ban đầu là ({v_0}) (feet/giây) tính từ chân mặt phẳng nghiêng tạo một góc ({45^ circ }) so với phương ngang (xem hình vẽ). Nếu bỏ qua sức cản của không khí thì quãng đường R (tính bằng feet, 1 feet=0,3048 m) mà vật di chuyển lên mặt phẳng nghiêng được cho bởi hàm số (Rleft( theta right) = frac{{v_0^2sqrt 2 }}{{16}}cos theta left( {si
Đề bài
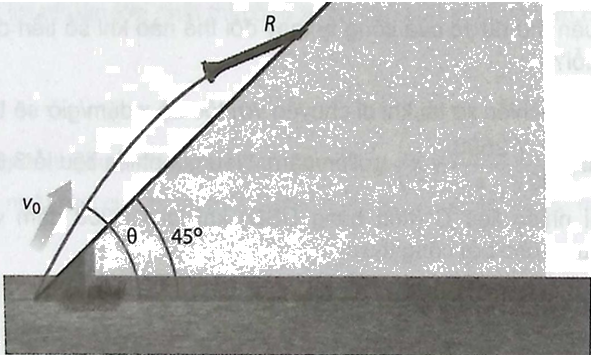
Một vật được phóng lên trời theo một góc xiên \(\theta \left( {{{45}^ \circ } < \theta < {{90}^ \circ }} \right)\) so với phương ngang với vận tốc ban đầu là \({v_0}\) (feet/giây) tính từ chân mặt phẳng nghiêng tạo một góc \({45^ \circ }\) so với phương ngang (xem hình vẽ). Nếu bỏ qua sức cản của không khí thì quãng đường R (tính bằng feet, 1 feet=0,3048 m) mà vật di chuyển lên mặt phẳng nghiêng được cho bởi hàm số
\(R\left( \theta \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos \theta \left( {\sin \theta - \cos \theta } \right)\)
Góc ném \(\theta \) nào làm cho quãng đường R lớn nhất? Giá trị lớn nhất của R là bao nhiêu?
Phương pháp giải - Xem chi tiết
Xét hàm số \(R\left( \theta \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos \theta \left( {\sin \theta - \cos \theta } \right)\). Yêu cầu bài toán tương đương tìm giá trị lớn nhất của hàm. Tính đạo hàm, lập bảng biến thiên của hàm số và đưa ra kết luận.
Lời giải chi tiết
Xét hàm số \(R\left( \theta \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos \theta \left( {\sin \theta - \cos \theta } \right)\). Ta cần tìm \(\theta \) để hàm số đạt giá trị lớn nhất.
Ta có \(R\left( \theta \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\left( {\cos \theta \sin \theta - {{\cos }^2}\theta } \right) = \frac{{v_0^2\sqrt 2 }}{{32}}\left( {2\cos \theta \sin \theta - 2{{\cos }^2}\theta } \right)\)
\( = \frac{{v_0^2\sqrt 2 }}{{32}}\left( {\sin 2\theta - \cos 2\theta - 1} \right)\), \(\left( {{{45}^ \circ } < \theta < {{90}^ \circ }} \right)\). Do đó \(R' = \frac{{v_0^2\sqrt 2 }}{{16}}\left( {\cos 2\theta + \sin 2\theta } \right)\).
Khi đó \(R' = 0 \Leftrightarrow \frac{{v_0^2\sqrt 2 }}{{16}}\left( {\cos 2\theta + \sin 2\theta } \right) = 0 \Leftrightarrow \cos 2\theta + \sin 2\theta = 0 \Leftrightarrow 2\theta = {135^ \circ } \Leftrightarrow \theta = {67,5^ \circ }\)
(do \({45^ \circ } < \theta < {90^ \circ }\)). Mặt khác \(R\left( {{{45}^ \circ }} \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos {45^ \circ }\left( {\sin {{45}^ \circ } - \cos {{45}^ \circ }} \right) = 0\); \(R\left( {{{67,5}^ \circ }} \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos {67,5^ \circ }\left( {\sin {{67,5}^ \circ } - \cos {{67,5}^ \circ }} \right) = \frac{{v_0^2\left( {2 - \sqrt 2 } \right)}}{{32}}\); \(R\left( {{{90}^ \circ }} \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos {90^ \circ }\left( {\sin {{90}^ \circ } - \cos {{90}^ \circ }} \right) = 0\).
Lập bảng biến thiên của hàm số:
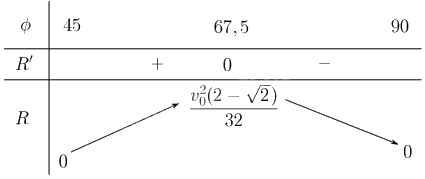
Từ bảng biến thiên suy ra hàm số đạt giá trị lớn nhất tại \(67,5\): \(\mathop {\max }\limits_{\left[ {45;90} \right]} R = R\left( {67,5} \right) = \frac{{v_0^2\left( {2 - \sqrt 2 } \right)}}{{32}}.\)
Vậy khi góc ném \(\theta = {67,5^ \circ }\) thì quãng đường R là lớn nhất và bằng \(\frac{{v_0^2\left( {2 - \sqrt 2 } \right)}}{{32}}\) feet.
Giải bài 1.19 trang 16 SBT Toán 12 - Kết nối tri thức: Tổng quan
Bài 1.19 trang 16 sách bài tập Toán 12 Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về hàm số, tập xác định, tập giá trị, tính đơn điệu và cực trị của hàm số để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và phương pháp giải là vô cùng quan trọng để đạt điểm cao trong các kỳ thi.
Nội dung bài tập 1.19
Bài 1.19 thường bao gồm các dạng bài tập sau:
- Xác định tập xác định của hàm số.
- Tìm tập giá trị của hàm số.
- Xét tính đơn điệu của hàm số.
- Tìm cực trị của hàm số.
- Vẽ đồ thị hàm số.
- Ứng dụng đồ thị hàm số để giải các bài toán liên quan.
Lời giải chi tiết bài 1.19 trang 16 SBT Toán 12 - Kết nối tri thức
Để giải bài 1.19 trang 16 SBT Toán 12 Kết nối tri thức, chúng ta cần thực hiện các bước sau:
- Bước 1: Đọc kỹ đề bài và xác định yêu cầu của bài toán.
- Bước 2: Xác định hàm số cần xét.
- Bước 3: Áp dụng các kiến thức và phương pháp đã học để giải quyết bài toán.
- Bước 4: Kiểm tra lại kết quả và đảm bảo tính chính xác.
Ví dụ minh họa:
Giả sử bài 1.19 yêu cầu tìm tập xác định của hàm số f(x) = √(x-2)/(x+1). Ta thực hiện như sau:
- Điều kiện xác định: x - 2 ≥ 0 và x + 1 ≠ 0
- Giải bất phương trình x - 2 ≥ 0, ta được x ≥ 2.
- Giải phương trình x + 1 ≠ 0, ta được x ≠ -1.
- Kết hợp hai điều kiện trên, ta có tập xác định của hàm số là: D = [2; +∞)
Mẹo giải bài tập Toán 12 hiệu quả
Để giải bài tập Toán 12 hiệu quả, các em có thể tham khảo một số mẹo sau:
- Nắm vững các định nghĩa, định lý và công thức quan trọng.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm vẽ đồ thị.
- Tham khảo các tài liệu tham khảo, sách giải bài tập.
- Hỏi thầy cô giáo hoặc bạn bè khi gặp khó khăn.
Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là một website cung cấp đầy đủ các tài liệu học tập Toán 12, bao gồm sách giáo khoa, sách bài tập, đề thi, lời giải chi tiết và các bài viết hướng dẫn giải bài tập. Chúng tôi cam kết cung cấp cho các em những tài liệu chất lượng, chính xác và dễ hiểu nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
Bảng tổng hợp các bài giải Toán 12 Kết nối tri thức
| Chương | Bài | Liên kết |
|---|---|---|
| 1 | 1.1 | Giải bài 1.1 |
| 1 | 1.2 | Giải bài 1.2 |
| ... | ... | ... |
Chúc các em học tập tốt và đạt kết quả cao!