Giải bài 1.11 trang 14 Sách bài tập Toán 12 - Kết nối tri thức

Giải bài 1.11 trang 14 sách bài tập toán 12 - Kết nối tri thức

Giải bài 1.11 trang 14 SBT Toán 12 Kết nối tri thức

Chào mừng các em học sinh đến với lời giải chi tiết bài 1.11 trang 14 sách bài tập Toán 12 Kết nối tri thức. Bài tập này thuộc chương trình học Toán 12, tập trung vào việc rèn luyện kỹ năng về giới hạn của hàm số.

tusach.vn cung cấp lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.

Sử dụng đồ thị dưới đây, xác định xem hàm số (y = fleft( x right)) có giá trị lớn nhất, giá trị nhỏ nhất hay cực trị tại mỗi điểm ({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8}) hay không.

Đề bài

Sử dụng đồ thị dưới đây, xác định xem hàm số \(y = f\left( x \right)\) có giá trị lớn nhất, giá trị nhỏ nhất hay cực trị tại mỗi điểm \({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8}\) hay không.

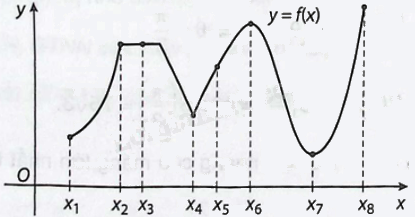
Giải bài 1.11 trang 14 sách bài tập toán 12 - Kết nối tri thức 1

Phương pháp giải - Xem chi tiết Giải bài 1.11 trang 14 sách bài tập toán 12 - Kết nối tri thức 2

Quan sát đồ thị kết hợp với định nghĩa cực trị, giá trị lớn nhất, nhỏ nhất của hàm số để đưa ra kết luận.

Lời giải chi tiết

Ta có hàm số \(y = f\left( x \right)\) xác định trên \(\left[ {{x_1};{x_8}} \right]\). Từ đồ thị ta có:

+ \(f\left( x \right) \le f\left( {{x_8}} \right)\) với mọi \(x \in \left[ {{x_1};{x_8}} \right]\) và \({x_8} \in \left[ {{x_1};{x_8}} \right]\) thỏa mãn \(f\left( x \right) = f\left( {{x_8}} \right)\). Do đó hàm số đạt giá trị lớn nhất tại điểm \({x_8}\).

+ \(f\left( x \right) \ge f\left( {{x_7}} \right)\) với mọi \(x \in \left[ {{x_1};{x_8}} \right]\) và \({x_7} \in \left[ {{x_1};{x_8}} \right]\) thỏa mãn \(f\left( x \right) = f\left( {{x_7}} \right)\). Do đó hàm số

đạt giá trị nhỏ nhất tại điểm \({x_7}\).

Ta có hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ {{x_1};{x_8}} \right]\).

+ Gọi \({h_1} = \frac{{{x_5} - {x_4}}}{2}\) , ta thấy \({h_1}\) dương. Vì \(f\left( x \right) > f\left( {{x_4}} \right)\) với mọi \(x \in \left( {{x_4} - {h_1};{x_4} + {h_1}} \right) \subset \left[ {{x_1};{x_8}} \right]\) và \(x \ne {x_4}\) nên hàm số đạt cực tiểu tại điểm \({x_4}\).

+ Tương tự, gọi \({h_2} = \frac{{{x_8} - {x_7}}}{2}\) , ta thấy \({h_2}\) dương. Vì \(f\left( x \right) > f\left( {{x_7}} \right)\) với mọi \(x \in \left( {{x_7} - {h_2};{x_7} + {h_2}} \right) \subset \left[ {{x_1};{x_8}} \right]\) và \(x \ne {x_7}\) nên hàm số đạt cực tiểu tại điểm \({x_7}\).

+ Gọi \({h_3} = \frac{{{x_6} - {x_5}}}{2}\) , ta thấy \({h_3}\) dương. Vì \(f\left( x \right) < f\left( {{x_6}} \right)\) với mọi \(x \in \left( {{x_6} - {h_3};{x_6} + {h_3}} \right) \subset \left[ {{x_1};{x_8}} \right]\) và \(x \ne {x_6}\) nên hàm số đạt cực đại tại điểm \({x_6}\).

Giải bài 1.11 trang 14 SBT Toán 12 Kết nối tri thức: Giới thiệu chung

Bài 1.11 trang 14 sách bài tập Toán 12 Kết nối tri thức yêu cầu học sinh tính giới hạn của hàm số tại một điểm cho trước. Đây là một dạng bài tập cơ bản nhưng quan trọng trong chương trình học về giới hạn. Việc nắm vững phương pháp giải bài tập này sẽ giúp học sinh hiểu sâu hơn về khái niệm giới hạn và ứng dụng của nó trong các bài toán thực tế.

Nội dung bài tập 1.11 trang 14 SBT Toán 12 Kết nối tri thức

Bài tập 1.11 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính giới hạn của các hàm số khác nhau. Các hàm số này có thể là hàm đa thức, hàm phân thức, hoặc các hàm số phức tạp hơn. Để giải bài tập này, học sinh cần nắm vững các quy tắc tính giới hạn, bao gồm:

Giới hạn của một tổng bằng tổng các giới hạn.
Giới hạn của một tích bằng tích các giới hạn.
Giới hạn của một thương bằng thương các giới hạn (với mẫu khác 0).
Giới hạn của một hàm số khi x tiến tới một giá trị cụ thể.

Lời giải chi tiết bài 1.11 trang 14 SBT Toán 12 Kết nối tri thức

Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 1.11:

Câu a)

Để tính lim_x→2 (x² - 4) / (x - 2), ta có thể phân tích tử số thành nhân tử:

(x² - 4) = (x - 2)(x + 2)

Do đó:

lim_x→2 (x² - 4) / (x - 2) = lim_x→2 (x - 2)(x + 2) / (x - 2) = lim_x→2 (x + 2) = 4

Câu b)

Để tính lim_x→1 (x³ - 1) / (x - 1), ta có thể phân tích tử số thành nhân tử:

(x³ - 1) = (x - 1)(x² + x + 1)

Do đó:

lim_x→1 (x³ - 1) / (x - 1) = lim_x→1 (x - 1)(x² + x + 1) / (x - 1) = lim_x→1 (x² + x + 1) = 3

Câu c)

(Giải tương tự như câu a và b)

Mẹo giải nhanh bài tập về giới hạn

Để giải nhanh các bài tập về giới hạn, học sinh có thể áp dụng một số mẹo sau:

Phân tích tử số và mẫu số thành nhân tử để rút gọn biểu thức.
Sử dụng các quy tắc tính giới hạn để đơn giản hóa bài toán.
Áp dụng định nghĩa giới hạn để chứng minh sự tồn tại của giới hạn.

Luyện tập thêm

Để củng cố kiến thức về giới hạn, học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. tusach.vn cung cấp đầy đủ các bài giải chi tiết và hướng dẫn giải bài tập Toán 12, giúp các em học tập hiệu quả.

Kết luận

Bài 1.11 trang 14 SBT Toán 12 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính giới hạn. Hy vọng với lời giải chi tiết và các mẹo giải nhanh trên, các em sẽ tự tin giải quyết bài tập này và các bài tập tương tự trong tương lai.