Giải bài 1.13 trang 14 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 1.13 trang 14 SBT Toán 12 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 1.13 trang 14 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu nhất.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = - {x^3} + 3{x^2} + 2); b) (y = frac{{{x^2}}}{{{x^2} + 2}}).
Đề bài
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = - {x^3} + 3{x^2} + 2\);
b) \(y = \frac{{{x^2}}}{{{x^2} + 2}}\).
Phương pháp giải - Xem chi tiết
- Tìm tập xác định của hàm số.
- Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng \(0\) hoặc đạo hàm không tồn tại.
- Lập bảng biến thiên của hàm số.
- Từ bảng biến thiên suy ra giá trị lớn nhất, nhỏ nhất (nếu có).
Lời giải chi tiết
a) Tập xác định: \(\mathbb{R}\)
Ta có \(y' = - 3{x^2} + 6x\). Khi đó \(y' = 0 \Leftrightarrow - 3{x^2} + 6x = 0 \Leftrightarrow x = 0\) hoặc \(x = 2\).
Lập bảng biến thiên của hàm số:
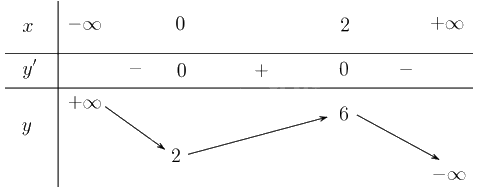
Từ bảng biến thiên thấy hàm số không có cả giá trị lớn nhất và giá trị nhỏ nhất.
b) Tập xác định: \(\mathbb{R}\)
Ta có \(y' = \frac{{1 \cdot \left( {{x^2} + 2} \right) - x \cdot 2x}}{{{{\left( {{x^2} + 2} \right)}^2}}} = \frac{{ - {x^2} + 2}}{{{{\left( {{x^2} + 2} \right)}^2}}}\).
Khi đó \(y' = 0 \Leftrightarrow \frac{{ - {x^2} + 2}}{{{{\left( {{x^2} + 2} \right)}^2}}} = 0 \Leftrightarrow - {x^2} + 2 = 0 \Leftrightarrow x = - \sqrt 2 \) hoặc \(x = \sqrt 2 \).
Lập bảng biến thiên của hàm số:
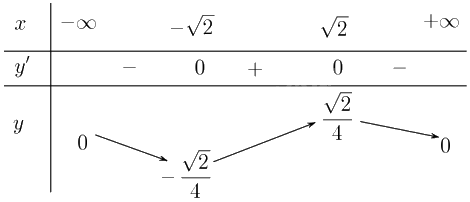
Từ bảng biến thiên, ta có: \(\mathop {\min }\limits_\mathbb{R} y = y\left( { - \sqrt 2 } \right) = \frac{{ - \sqrt 2 }}{4}\); \(\mathop {\max }\limits_\mathbb{R} y = y\left( {\sqrt 2 } \right) = \frac{{\sqrt 2 }}{4}\).
Giải bài 1.13 trang 14 SBT Toán 12 - Kết nối tri thức: Tổng quan
Bài 1.13 trang 14 sách bài tập Toán 12 Kết nối tri thức thuộc chương 1: Giới hạn – Sự liên tục. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể. Việc hiểu rõ định nghĩa giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn là rất quan trọng để hoàn thành tốt bài tập này.
Nội dung bài 1.13 trang 14 SBT Toán 12 - Kết nối tri thức
Bài 1.13 thường bao gồm các dạng bài tập sau:
- Tính giới hạn của hàm số tại một điểm.
- Tính giới hạn của hàm số khi x tiến tới vô cùng.
- Sử dụng định nghĩa giới hạn để chứng minh một khẳng định.
- Ứng dụng giới hạn vào việc xét tính liên tục của hàm số.
Lời giải chi tiết bài 1.13 trang 14 SBT Toán 12 - Kết nối tri thức
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài 1.13:
Ví dụ minh họa (Giả sử bài 1.13 là tính giới hạn của hàm số f(x) = (x^2 - 1)/(x - 1) khi x tiến tới 1)
Lời giải:
Ta có:
lim (x→1) f(x) = lim (x→1) (x^2 - 1)/(x - 1)
= lim (x→1) (x - 1)(x + 1)/(x - 1)
= lim (x→1) (x + 1)
= 1 + 1 = 2
Vậy, lim (x→1) f(x) = 2
Mẹo giải bài tập về giới hạn
Để giải các bài tập về giới hạn một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
- Phân tích tử và mẫu thành nhân tử để rút gọn biểu thức.
- Sử dụng các công thức giới hạn cơ bản.
- Áp dụng quy tắc L'Hôpital khi gặp dạng vô định.
- Biến đổi biểu thức về dạng quen thuộc để dễ dàng tính giới hạn.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa và sách bài tập, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về giới hạn:
- Các bài giảng trực tuyến về giới hạn.
- Các trang web và diễn đàn toán học uy tín.
- Các bài tập trắc nghiệm và tự luận về giới hạn.
Kết luận
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn khi giải bài 1.13 trang 14 SBT Toán 12 Kết nối tri thức và các bài tập tương tự. Chúc các em học tập tốt!
| Công thức giới hạn quan trọng | Ví dụ |
|---|---|
| lim (x→0) sin(x)/x = 1 | Tính giới hạn lim (x→0) sin(2x)/x |
| lim (x→0) (1 - cos(x))/x^2 = 1/2 | Tính giới hạn lim (x→0) (1 - cos(3x))/x^2 |