Giải bài 1.32 trang 25 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 1.32 trang 25 SBT Toán 12 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 1.32 trang 25 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu nhất.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) (y = frac{{3x + 5}}{{x + 2}}); b) (y = frac{{2x - 1}}{{x - 1}}).
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{3x + 5}}{{x + 2}}\);
b) \(y = \frac{{2x - 1}}{{x - 1}}\).
Phương pháp giải - Xem chi tiết
+ Tìm tập xác định của hàm số.
+ Khảo sát sự biến thiên của hàm số: Tính đạo hàm, tìm các khoảng đồng biến, nghịch biến của đồ thị, tìm các điểm cực trị, cực trị, tiệm cận, ghi kết quả tìm được vào bảng biến thiên.
+ Vẽ đồ thị dựa vào bảng biến thiên, khi vẽ lưu ý đến tính đối xứng, tọa độ giao điểm với các trục.
Lời giải chi tiết
a) Tập xác định: \(\mathbb{R}\backslash \left\{ { - 2} \right\}\)
Sự biến thiên:
+ Ta có \(y' = \frac{1}{{{{\left( {x + 2} \right)}^2}}} > 0\) với mọi \(x \ne - 2\).
+ Hàm số đồng biến trên từng khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
+ Hàm số không có cực trị.
+ Tiệm cận: \(\mathop {\lim }\limits_{x \to + \infty } = 3\) suy ra tiệm cận ngang là đường thẳng \(y = 3\); \(\mathop {\lim }\limits_{x \to - {2^ + }} y = + \infty ;\mathop {\lim }\limits_{x \to - {2^ - }} y = - \infty \) suy ra tiệm cận đứng là đường thẳng \(x = - 2\).
+ Bảng biến thiên:
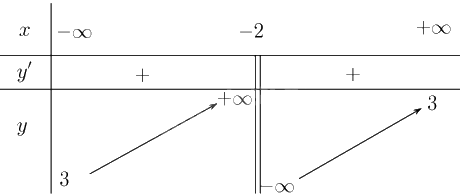
Đồ thị: Đồ thị của hàm số cắt trục tung tại điểm \(\left( {0;\frac{5}{2}} \right)\), cắt trục hoành tại hai điểm \(\left( {\frac{{ - 5}}{3};0} \right)\) và \(\left( {3;0} \right)\). Đồ thị nhận \(\left( { - 2;3} \right)\) làm tâm đối xứng. Hai trục đối xứng của hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận.
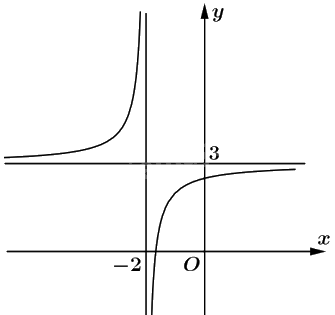
b) Tập xác định: \(\mathbb{R}\backslash \left\{ 1 \right\}\).
Sự biến thiên:
+ Ta có \(y' = \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}} < 0\) với mọi \(x \ne 1\).
+ Hàm số nghịch biến trên từng khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
+ Hàm số không có cực trị.
+ Tiệm cận: \(\mathop {\lim }\limits_{x \to + \infty } y = 2\) suy ra tiệm cận ngang là đường thẳng \(y = 2\); \(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty \) suy ra tiệm cận đứng là đường thẳng \(x = 1\).
+ Bảng biến thiên:
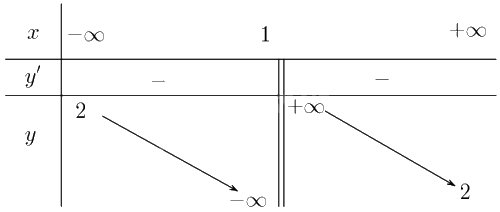
Đồ thị: Đồ thị của hàm số cắt trục tung tại điểm \(\left( {0;1} \right)\), cắt trục hoành tại điểm \(\left( {\frac{1}{2};0} \right)\), đồ thị có tâm đối xứng là điểm \(\left( {1;2} \right)\). Hai trục đối xứng của hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận.
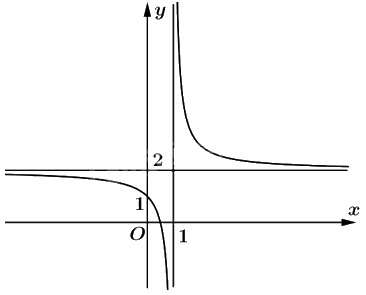
Giải bài 1.32 trang 25 SBT Toán 12 - Kết nối tri thức: Tổng quan
Bài 1.32 trang 25 sách bài tập Toán 12 Kết nối tri thức thuộc chương 1: Hàm số lượng giác và đồ thị. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác, đặc biệt là các phép biến đổi lượng giác để giải quyết các bài toán thực tế hoặc chứng minh các đẳng thức.
Nội dung bài tập 1.32
Bài 1.32 thường bao gồm các dạng bài tập sau:
- Tìm tập xác định của hàm số lượng giác: Yêu cầu xác định điều kiện để hàm số có nghĩa, thường liên quan đến mẫu số khác 0 hoặc biểu thức trong căn bậc hai lớn hơn hoặc bằng 0.
- Biến đổi lượng giác: Sử dụng các công thức lượng giác cơ bản để biến đổi biểu thức, đơn giản hóa hàm số hoặc chứng minh đẳng thức.
- Giải phương trình lượng giác: Vận dụng các phương pháp giải phương trình lượng giác đã học để tìm nghiệm của phương trình.
- Ứng dụng hàm số lượng giác vào thực tế: Giải các bài toán liên quan đến các hiện tượng thực tế như dao động điều hòa, sóng ánh sáng, v.v.
Lời giải chi tiết bài 1.32 trang 25 SBT Toán 12 - Kết nối tri thức
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài 1.32. (Ở đây sẽ là lời giải chi tiết của bài tập 1.32, bao gồm các bước giải, giải thích và kết luận.)
Ví dụ minh họa
Ví dụ: Cho hàm số y = tan(2x + π/3). Tìm tập xác định của hàm số.
Lời giải:
Hàm số y = tan(2x + π/3) xác định khi và chỉ khi cos(2x + π/3) ≠ 0.
Điều này tương đương với 2x + π/3 ≠ π/2 + kπ, với k là số nguyên.
Suy ra 2x ≠ π/6 + kπ, hay x ≠ π/12 + kπ/2, với k là số nguyên.
Vậy tập xác định của hàm số là D = R \ {π/12 + kπ/2, k ∈ Z}.
Mẹo giải bài tập hàm số lượng giác
- Nắm vững các công thức lượng giác: Đây là nền tảng để giải quyết các bài toán biến đổi lượng giác.
- Sử dụng các phương pháp đại số: Đặt ẩn phụ, phân tích đa thức thành nhân tử, v.v.
- Kiểm tra lại kết quả: Đảm bảo rằng nghiệm tìm được thỏa mãn điều kiện của bài toán.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải toán.
Tài liệu tham khảo
Ngoài sách bài tập, các em có thể tham khảo thêm các tài liệu sau:
- Sách giáo khoa Toán 12 - Kết nối tri thức
- Các trang web học toán trực tuyến
- Các video bài giảng trên YouTube
Kết luận
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập trên, các em sẽ tự tin hơn khi giải bài 1.32 trang 25 sách bài tập Toán 12 Kết nối tri thức và các bài tập tương tự. Chúc các em học tốt!