Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 1.4 trang 9 sách bài tập toán 12 - Kết nối tri thức
SBT Toán 12 - Kết nối tri thức
SBT TOÁN TẬP 1 - KẾT NỐI TRI THỨC
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Bài 1. Tính đơn điệu và cực trị của hàm số

Giải bài 1.4 trang 9 sách bài tập toán 12 - Kết nối tri thức

Giải bài 1.4 trang 9 SBT Toán 12 - Kết nối tri thức

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài 1.4 trang 9 một cách dễ hiểu nhất.

Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Tìm các khoảng đơn điệu và các cực trị (nếu có) của các hàm số sau: a) (y = {x^4} - 2{x^2} + 3); b) (y = {x^2}ln x).

Đề bài

Tìm các khoảng đơn điệu và các cực trị (nếu có) của các hàm số sau:

a) \(y = {x^4} - 2{x^2} + 3\);

b) \(y = {x^2}\ln x\).

Phương pháp giải - Xem chi tiếtGiải bài 1.4 trang 9 sách bài tập toán 12 - Kết nối tri thức 1

Ý a:

- Tìm tập xác định của hàm số.

- Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng \(0\).

- Lập bảng biến thiên của hàm số.

- Từ bảng biến thiên suy ra các khoảng đồng biến, nghịch biến, cực trị của hàm số.

Ý b:

- Tìm tập xác định của hàm số.

- Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng \(0\).

- Lập bảng biến thiên của hàm số.

- Từ bảng biến thiên suy ra các khoảng đồng biến, nghịch biến, cực trị của hàm số.

Lời giải chi tiết

a) Tập xác định: \(\mathbb{R}\)

Ta có \(y' = 4{x^3} - 4x\). Khi đó \(y' = 0 \Leftrightarrow 4{x^3} - 4x = 0 \Leftrightarrow {x^3} - x = 0 \Leftrightarrow x = - 1\) hoặc \(x = 0\) hoặc \(x = 1\).

Lập bảng biến thiên của hàm số:

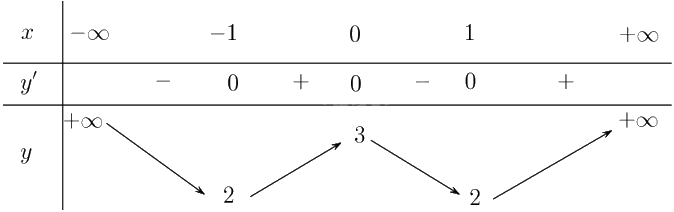
Giải bài 1.4 trang 9 sách bài tập toán 12 - Kết nối tri thức 2

Từ bảng biến thiên, ta có:

Hàm số đồng biến trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).

Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).

Hàm số đạt cực đại tại \(x = 0\) và \({y_{CĐ}} = y\left( { 0} \right) = 3\).

Hàm số đạt cực tiểu tại \(x = - 1\) và \({y_{CT}} = y\left( { - 1} \right) = 2\).

Hàm số đạt cực tiểu tại \(x = 1\) và \({y_{CT}} = y\left( 1 \right) = 2\).

b) Tập xác định: \(\left( {0; + \infty } \right)\)

Ta có \(y' = 2x\ln x + x\). Khi đó \(y' = 0 \Leftrightarrow 2x\ln x + x = 0 \Leftrightarrow \ln x = - \frac{1}{2} \Leftrightarrow x = {e^{ - \frac{1}{2}}}\)

Lập bảng biến thiên của hàm số:

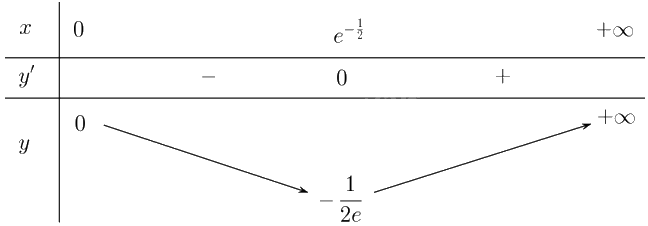
Giải bài 1.4 trang 9 sách bài tập toán 12 - Kết nối tri thức 3

Từ bảng biến thiên, ta có:

Hàm số đồng biến trên khoảng \(\left( {{e^{ - \frac{1}{2}}}; + \infty } \right)\). Hàm số nghịch biến trên khoảng \(\left( {0;{e^{ - \frac{1}{2}}}} \right)\).

Hàm số đạt cực tiểu tại \(x = {e^{ - \frac{1}{2}}}\) và \({y_{CT}} = y\left( {{e^{ - \frac{1}{2}}}} \right) = - \frac{1}{{2e}}\).

Giải bài 1.4 trang 9 SBT Toán 12 - Kết nối tri thức: Chi tiết và Dễ hiểu

Bài 1.4 trang 9 sách bài tập Toán 12 Kết nối tri thức thuộc chương 1: Giới hạn. Dưới đây là lời giải chi tiết bài tập này, giúp các em học sinh hiểu rõ phương pháp và áp dụng vào các bài tập tương tự.

Nội dung bài tập 1.4 trang 9 SBT Toán 12 - Kết nối tri thức

Bài tập yêu cầu tính giới hạn của hàm số khi x tiến tới một giá trị nhất định. Để giải bài tập này, chúng ta cần nắm vững các quy tắc tính giới hạn, đặc biệt là giới hạn của các hàm số đơn giản như đa thức, phân thức.

Lời giải chi tiết bài 1.4 trang 9 SBT Toán 12 - Kết nối tri thức

(Giả sử bài tập cụ thể là: Tính lim (x->2) (x^2 - 4) / (x - 2) )

  1. Phân tích tử thức: x2 - 4 = (x - 2)(x + 2)
  2. Viết lại biểu thức: (x2 - 4) / (x - 2) = [(x - 2)(x + 2)] / (x - 2)
  3. Rút gọn biểu thức: Khi x ≠ 2, ta có thể rút gọn biểu thức thành x + 2
  4. Tính giới hạn: lim (x->2) (x + 2) = 2 + 2 = 4

Vậy, lim (x->2) (x2 - 4) / (x - 2) = 4

Các dạng bài tập giới hạn thường gặp

  • Giới hạn của hàm đa thức: Thay trực tiếp giá trị của x vào hàm số.
  • Giới hạn của hàm phân thức: Cần xét cả tử thức và mẫu thức. Nếu mẫu thức khác 0 tại giá trị giới hạn, có thể thay trực tiếp. Nếu mẫu thức bằng 0, cần phân tích tử và mẫu để rút gọn.
  • Giới hạn vô cùng: Sử dụng các quy tắc chia cả tử và mẫu cho lũy thừa cao nhất của x.

Mẹo giải bài tập giới hạn hiệu quả

  • Nắm vững định nghĩa giới hạn: Hiểu rõ khái niệm giới hạn là gì để có thể áp dụng vào các bài tập.
  • Thành thạo các quy tắc tính giới hạn: Biết cách sử dụng các quy tắc để đơn giản hóa bài toán.
  • Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.

Tusach.vn - Đồng hành cùng bạn học Toán 12

Tusach.vn cung cấp đầy đủ lời giải sách bài tập Toán 12 Kết nối tri thức, cùng với các bài giảng video và tài liệu ôn tập hữu ích. Hãy truy cập tusach.vn để học Toán 12 hiệu quả hơn!

Ngoài ra, bạn có thể tham khảo thêm các bài giải khác trong chương 1: Giới hạn tại Tusach.vn.

Bài tậpLink
Bài 1.1Link bài 1.1
Bài 1.2Link bài 1.2

Chúc các bạn học tốt!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN