Giải bài 4.11 trang 12 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 4.11 trang 12 SBT Toán 12 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 4.11 trang 12 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu nhất.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Sử dụng ý nghĩa hình học của tích phân, tính: a) (intlimits_0^3 {left( {2x + 1} right)dx} ); b) (intlimits_0^4 {sqrt {16 - {x^2}} dx} ).
Đề bài
Sử dụng ý nghĩa hình học của tích phân, tính:
a) \(\int\limits_0^3 {\left( {2x + 1} \right)dx} \);
b) \(\int\limits_0^4 {\sqrt {16 - {x^2}} dx} \).
Phương pháp giải - Xem chi tiết
Ý a: Giá trị tích phân là diện tích của hình vẽ giới hạn bởi hàm \(2x + 1\) và hai đường thẳng xác định bởi giá trị hai cận do hàm không âm trên \(\left[ {0;3} \right]\).
Xác định hình vẽ đó và tính diện tích bằng công thức hình học.
Ý b: Giá trị tích phân là diện tích của hình vẽ giới hạn bởi hàm \(\sqrt {16 - {x^2}} \) và hai đường thẳng xác định bởi giá trị hai cận do hàm không âm trên \(\left[ {0;4} \right]\).
Xác định hình vẽ đó và tính diện tích bằng công thức hình học.
Lời giải chi tiết
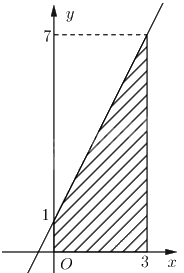
a) Ta có hàm số \(f\left( x \right) = 2x + 1\) không âm trên đoạn \(\left[ {0;3} \right]\). Do đó tích phân \(\int\limits_0^3 {\left( {2x + 1} \right)dx} \) là
diện tích của hình vẽ giới hạn bởi đồ thị \(y = f\left( x \right)\) và hai đường thẳng \(x = 0\) (trục \(Ox\)) và
\(x = 3\) như hình vẽ bên.Ta cần tính diện tích hình thang vuông có
đáy lớn là 7, đáy bé là 1 và chiều cao là 3.
Suy ra \(\int\limits_0^3 {\left( {2x + 1} \right)dx} = \frac{1}{2} \cdot \left( {1 + 7} \right) \cdot 3 = 12\).
b) Ta có \(\int\limits_0^4 {\sqrt {16 - {x^2}} dx} \).
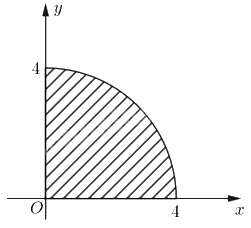
Ta có hàm số \(f\left( x \right) = \sqrt {16 - {x^2}} \) không âm trên đoạn \(\left[ {0;4} \right]\). Do đó tích phân \(\int\limits_0^3 {\left( {2x + 1} \right)dx} \) là diện tích của hình vẽ giới hạn bởi đồ thị \(y = f\left( x \right)\) và hai đường thẳng \(x = 0\) (trục \(Ox\)) và \(x = 4\) như hình vẽ bên.
Ta cần tính diện tích một phần tư đường tròn có bán kính là 4, tâm O nằm ở góc phần tư thứ I. Suy ra \(\int\limits_0^4 {\sqrt {16 - {x^2}} dx} = \frac{1}{4} \cdot \pi \cdot {4^2} = 4\pi \).
Giải bài 4.11 trang 12 SBT Toán 12 - Kết nối tri thức: Tổng quan và Phương pháp
Bài 4.11 trang 12 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế, hoặc chứng minh các đẳng thức liên quan đến đạo hàm.
Nội dung bài tập 4.11
Thông thường, bài 4.11 sẽ yêu cầu:
- Tính đạo hàm của một hàm số cho trước.
- Tìm đạo hàm cấp hai của một hàm số.
- Xác định các điểm cực trị của hàm số.
- Giải các bài toán liên quan đến ứng dụng của đạo hàm (ví dụ: tìm khoảng đơn điệu, cực trị, giá trị lớn nhất, giá trị nhỏ nhất của hàm số).
Phương pháp giải bài tập 4.11
Để giải quyết bài tập 4.11 một cách hiệu quả, các em cần nắm vững các kiến thức sau:
- Các quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Đạo hàm của các hàm số cơ bản: Đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit.
- Ứng dụng của đạo hàm: Khảo sát hàm số, tìm cực trị, giải phương trình, bất phương trình.
Lời giải chi tiết bài 4.11 trang 12 SBT Toán 12 - Kết nối tri thức
(Ở đây sẽ là lời giải chi tiết của bài tập 4.11. Ví dụ):
Bài 4.11: Cho hàm số y = x3 - 3x2 + 2. Tìm đạo hàm của hàm số và xác định các điểm cực trị.
Lời giải:
Đạo hàm của hàm số là: y' = 3x2 - 6x.
Để tìm các điểm cực trị, ta giải phương trình y' = 0:
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2.
Ta có bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Vậy hàm số đạt cực đại tại x = 0, ycđ = 2 và đạt cực tiểu tại x = 2, yct = -2.
Luyện tập thêm
Để củng cố kiến thức, các em có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 12 Kết nối tri thức và các đề thi thử Toán 12.
Kết luận
Bài 4.11 trang 12 SBT Toán 12 Kết nối tri thức là một bài tập quan trọng giúp các em hiểu sâu hơn về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn khi giải các bài tập tương tự.
Tusach.vn luôn cập nhật lời giải các bài tập Toán 12 mới nhất. Hãy truy cập website của chúng tôi để được hỗ trợ tốt nhất!