Giải bài 1.49 trang 32 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 1.49 trang 32 SBT Toán 12 Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết bài 1.49 trang 32 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác và đầy đủ nhất, đồng thời giải thích rõ ràng từng bước để bạn có thể hiểu sâu sắc về bài toán.
a) Nếu \(C\left( x \right)\) (USD) là chi phí sản xuất \(x\) đơn vị hàng hóa, thì chi phí trung bình cho mỗi đơn vị là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x}\). Chứng minh rằng nếu chi phí trung bình là nhỏ nhất thì chi phí biên bằng chi phí trung bình. b) Nếu \(C\left( x \right) = 16000 + 200x + 4{x^{\frac{3}{2}}}\), hãy tìm: (i) Chi phí, chi phí trung bình và chi phí biên khi sản xuất \(100\) đơn vị hàng hóa; (ii) Mức sản xuất mà khi đó sẽ giảm thiểu chi phí trung bì
Đề bài
a) Nếu \(C\left( x \right)\) (USD) là chi phí sản xuất \(x\) đơn vị hàng hóa, thì chi phí trung bình cho mỗi đơn vị là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x}\). Chứng minh rằng nếu chi phí trung bình là nhỏ nhất thì chi phí biên bằng chi phí trung bình.
b) Nếu \(C\left( x \right) = 16000 + 200x + 4{x^{\frac{3}{2}}}\), hãy tìm:
(i) Chi phí, chi phí trung bình và chi phí biên khi sản xuất \(100\) đơn vị hàng hóa;
(ii) Mức sản xuất mà khi đó sẽ giảm thiểu chi phí trung bình;
(iii) Chi phí trung bình nhỏ nhất.
Phương pháp giải - Xem chi tiết
Ý a: Tính \(\overline {C'} \left( x \right)\), sử dụng ý nghĩa của cực tiểu để chứng minh.
Ý b: Xác định công thức các hàm \(\overline C \left( x \right)\), \(C'\left( x \right)\).
(i) Thay \(x = 100\) vào các hàm \(C\left( x \right)\), \(\overline C \left( x \right)\), \(C'\left( x \right)\).
(ii) Khảo sát sự biến thiên của hàm \(\overline C \left( x \right)\), xác định khoảng mà hàm nghịch biến từ đó ruy ra mức sản xuất x.
(iii) Tìm giá trị nhỏ nhất của hàm số \(\overline C \left( x \right)\).
Lời giải chi tiết
a) Ta có \(\overline {C'} \left( x \right) = {\left[ {\frac{{C\left( x \right)}}{x}} \right]^\prime } = \frac{{C'\left( x \right) \cdot x - C\left( x \right)}}{{{x^2}}}\).
Chi phí trung bình nhỏ nhất khi \(\overline {C'} \left( x \right) = 0\) hay \(C'\left( x \right) \cdot x - C\left( x \right) = 0 \Leftrightarrow C'\left( x \right) = \frac{{C\left( x \right)}}{x}\).
Nói cách khác chi phí biên bằng chi phí trung bình.
b) Xét hàm số \(C\left( x \right) = 16000 + 200x + 4{x^{\frac{3}{2}}}\).
Ta có hàm chi phí trung bình là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{16000 + 200x + 4{x^{\frac{3}{2}}}}}{x} = \frac{{16000}}{x} + 200 + 4{x^{\frac{1}{2}}}\).
Hàm chi phí biên là \(C'\left( x \right) = 200 + 6{x^{\frac{1}{2}}}\).
(i) Ta có \(C\left( {100} \right) = 16000 + 200 \cdot 100 + 4 \cdot {100^{\frac{3}{2}}} = 40000\); \(\overline C \left( {100} \right) = \frac{{16000}}{{100}} + 200 + 4 \cdot {100^{\frac{1}{2}}} = 400\);
\(C'\left( {100} \right) = 200 + 6 \cdot {100^{\frac{1}{2}}} = 260\).
Vậy chi phí, chi phí trung bình và chi phí biên ở mức sản xuất 100 đơn vị hàng hóa lần lượt là \(40000\) USD, \(400\) USD và \(260\) USD.
(ii) Ta có \(\overline {C'} \left( x \right) = \frac{{ - 16000}}{{{x^2}}} + 2{x^{ - \frac{1}{2}}}\) khi đó \(\overline {C'} \left( x \right) = 0 \Leftrightarrow \frac{{ - 16000}}{{{x^2}}} + 2{x^{ - \frac{1}{2}}} = 0 \Leftrightarrow x = 400\) do \(x > 0\).
Lập bảng biến thiên
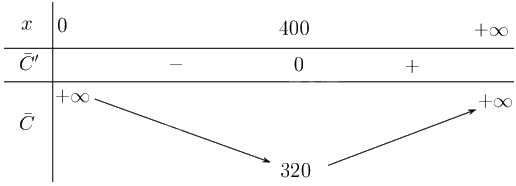
Từ bảng biến thiên suy ra, mức sản xuất là 400 đơn vị hàng hóa thì sẽ giảm thiểu giá trị trung bình.
(iii) Chi phí trung bình nhỏ nhất là 320 USD.
Giải bài 1.49 trang 32 SBT Toán 12 Kết nối tri thức: Chi tiết và Dễ hiểu
Bài 1.49 trang 32 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này thường liên quan đến việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và các bước thực hiện để bạn có thể hiểu rõ hơn về cách giải bài tập này.
Đề bài:
(Giả sử đề bài là: Cho hàm số y = f(x) có đạo hàm f'(x) = 3x2 - 6x + 1. Tìm điểm cực trị của hàm số.)
Lời giải:
Để tìm điểm cực trị của hàm số y = f(x), ta cần thực hiện các bước sau:
- Bước 1: Tìm đạo hàm bậc nhất f'(x).
- Bước 2: Giải phương trình f'(x) = 0 để tìm các điểm nghi ngờ là cực trị.
- Bước 3: Xét dấu đạo hàm f'(x) để xác định loại cực trị.
Áp dụng vào bài toán:
Ta có f'(x) = 3x2 - 6x + 1.
Giải phương trình f'(x) = 0:
3x2 - 6x + 1 = 0
Sử dụng công thức nghiệm của phương trình bậc hai, ta có:
x1 = (6 + √24) / 6 = 1 + √6 / 3
x2 = (6 - √24) / 6 = 1 - √6 / 3
Xét dấu đạo hàm f'(x):
- Khi x < 1 - √6 / 3, f'(x) > 0, hàm số đồng biến.
- Khi 1 - √6 / 3 < x < 1 + √6 / 3, f'(x) < 0, hàm số nghịch biến.
- Khi x > 1 + √6 / 3, f'(x) > 0, hàm số đồng biến.
Vậy, hàm số đạt cực đại tại x = 1 - √6 / 3 và đạt cực tiểu tại x = 1 + √6 / 3.
Lưu ý quan trọng:
Khi giải các bài toán về đạo hàm, bạn cần nắm vững các công thức đạo hàm cơ bản và các quy tắc tính đạo hàm. Ngoài ra, việc xét dấu đạo hàm là bước quan trọng để xác định loại cực trị của hàm số.
Các bài tập tương tự:
Để luyện tập thêm, bạn có thể tham khảo các bài tập tương tự trong sách bài tập Toán 12 Kết nối tri thức hoặc trên các trang web học toán trực tuyến.
Kết luận:
Hy vọng với lời giải chi tiết này, bạn đã hiểu rõ cách giải bài 1.49 trang 32 SBT Toán 12 Kết nối tri thức. Chúc bạn học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Đạo hàm | Tốc độ thay đổi của hàm số tại một điểm. |
| Điểm cực trị | Điểm mà tại đó hàm số đạt cực đại hoặc cực tiểu. |
Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại để lại bình luận bên dưới. tusach.vn luôn sẵn sàng hỗ trợ bạn!