Giải bài 1.50 trang 33 Sách bài tập Toán 12 - Kết nối tri thức

Giải bài 1.50 trang 33 sách bài tập toán 12 - Kết nối tri thức

Giải bài 1.50 trang 33 SBT Toán 12 Kết nối tri thức

Chào mừng các em học sinh đến với lời giải chi tiết bài 1.50 trang 33 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.

a) Chứng tỏ rằng nếu lợi nhuận (Pleft( x right)) là cực đại thì doanh thu biên bằng chi phí biên. b) Cho (Cleft( x right) = 16000 + 500x - 1,6{x^2} + 0,004{x^3}) là hàm chi phí và (pleft( x right) = 1700 - 7x) là hàm cầu. Hãy tìm mức sản xuất sẽ tối đa lợi nhuận.

Đề bài

a) Chứng tỏ rằng nếu lợi nhuận \(P\left( x \right)\) là cực đại thì doanh thu biên bằng chi phí biên.

b) Cho \(C\left( x \right) = 16000 + 500x - 1,6{x^2} + 0,004{x^3}\) là hàm chi phí và \(p\left( x \right) = 1700 - 7x\) là hàm cầu. Hãy tìm mức sản xuất sẽ tối đa lợi nhuận.

Phương pháp giải - Xem chi tiết Giải bài 1.50 trang 33 sách bài tập toán 12 - Kết nối tri thức 1

Ý a: Tính hàm lợi nhuận \(P\left( x \right) = R\left( x \right) - C\left( x \right)\), tính đạo hàm và sử dụng ý nghĩa của cực đại.

Ý b: Xác định công thức hàm lợi nhuận \(P\left( x \right) = x \cdot p\left( x \right) - C\left( x \right)\) và tìm giá trị lớn nhất.

Lời giải chi tiết

a) Ta có hàm lợi nhuận \(P\left( x \right) = R\left( x \right) - C\left( x \right)\) trong đó \(R\left( x \right)\) là doanh thu và \(C\left( x \right)\) là chi phí.

Khi lợi nhuận đạt cực đại tại \({x_0}\) thì \(P'\left( {{x_0}} \right) = R'\left( {{x_0}} \right) - C'\left( {{x_0}} \right) = 0\) hay \(R'\left( {{x_0}} \right) = C'\left( {{x_0}} \right)\). Nói cách khác doanh thu biên bằng chi phí biên.

b) Ta có hàm lợi nhuận

\(\begin{array}{l}P\left( x \right) = x \cdot p\left( x \right) - C\left( x \right) = x\left( {1700 - 7x)} \right) - \left( {16000 + 500x - 1,6{x^2} + 0,004{x^3}} \right)\ = - 16000 + 1200x - 5,4{x^2} - 0,004{x^3}\end{array}\)

Suy ra \(P'\left( x \right) = 1200 - 10,8x - 0,012{x^2}\) khi đó \(P'\left( x \right) = 0 \Leftrightarrow 1200 - 10,8x - 0,012{x^2} = 0 \Leftrightarrow x = 100\) do \(x > 0\).

Lập bảng biến thiên

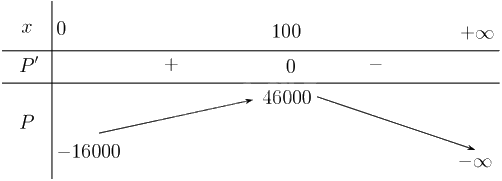
Giải bài 1.50 trang 33 sách bài tập toán 12 - Kết nối tri thức 2

Vậy mức sản xuất tối đa là 100 đơn vị hàng hóa.

Giải bài 1.50 trang 33 SBT Toán 12 Kết nối tri thức: Tổng quan và Phương pháp

Bài 1.50 trang 33 sách bài tập Toán 12 Kết nối tri thức là một bài tập thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số để giải quyết các bài toán cụ thể.

Nội dung bài tập 1.50 trang 33 SBT Toán 12 Kết nối tri thức

Thông thường, bài 1.50 sẽ yêu cầu:

Tính đạo hàm của một hàm số cho trước.
Tìm đạo hàm cấp hai của một hàm số.
Xác định các điểm cực trị của hàm số.
Khảo sát sự biến thiên của hàm số.

Phương pháp giải bài tập 1.50 trang 33 SBT Toán 12 Kết nối tri thức

Để giải quyết bài tập này một cách hiệu quả, các em cần nắm vững các kiến thức sau:

Công thức đạo hàm cơ bản: Nắm vững đạo hàm của các hàm số cơ bản như hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit.
Quy tắc đạo hàm: Hiểu rõ và áp dụng thành thạo các quy tắc đạo hàm như quy tắc cộng, trừ, nhân, chia, quy tắc chuỗi.
Đạo hàm cấp hai: Biết cách tính đạo hàm cấp hai của một hàm số bằng cách lấy đạo hàm của đạo hàm cấp nhất.
Điều kiện cực trị: Nắm vững điều kiện cần và đủ để một điểm là điểm cực trị của hàm số.

Lời giải chi tiết bài 1.50 trang 33 SBT Toán 12 Kết nối tri thức (Ví dụ minh họa)

Bài tập: Tính đạo hàm của hàm số f(x) = x³ + 2x² - 5x + 1.

Lời giải:

f'(x) = 3x² + 4x - 5

Các dạng bài tập tương tự và cách giải

Ngoài bài tập 1.50, các em có thể gặp các bài tập tương tự với các hàm số khác nhau. Để giải quyết các bài tập này, các em chỉ cần áp dụng các kiến thức và phương pháp đã học ở trên.

Mẹo giải nhanh bài tập đạo hàm

Sử dụng bảng đạo hàm cơ bản để tiết kiệm thời gian.
Luyện tập thường xuyên để nắm vững các quy tắc đạo hàm.
Kiểm tra lại kết quả sau khi tính toán.

Tài liệu tham khảo hữu ích

Các em có thể tham khảo thêm các tài liệu sau để học tốt môn Toán:

Sách giáo khoa Toán 12 Kết nối tri thức.
Sách bài tập Toán 12 Kết nối tri thức.
Các trang web học Toán trực tuyến uy tín như Tusach.vn.

Kết luận

Hy vọng với lời giải chi tiết và phương pháp giải bài tập 1.50 trang 33 SBT Toán 12 Kết nối tri thức này, các em sẽ hiểu rõ hơn về đạo hàm và tự tin hơn trong quá trình học tập. Chúc các em học tốt!