Giải bài 1.35 trang 25 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 1.35 trang 25 SBT Toán 12 - Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết bài 1.35 trang 25 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác và đầy đủ nhất, đồng thời giải thích rõ ràng từng bước để bạn có thể hiểu sâu sắc về bài toán.
Gia tốc \(a\left( t \right)\) của một vật chuyển động, \(t\) tính theo giây, từ giây thứ nhất đến giây thứ \(5\) là một hàm liên tục có đồ thị như sau: a) Lập bảng biến thiên của hàm vận tốc \(y = v\left( t \right)\) của vật, với \(t \in \left[ {1;5} \right]\). b) Tại thời điểm nào vật chuyển động với vận tốc lớn nhất?
Đề bài
Gia tốc \(a\left( t \right)\) của một vật chuyển động, \(t\) tính theo giây, từ giây thứ nhất đến giây thứ \(5\) là một hàm liên tục có đồ thị như sau:
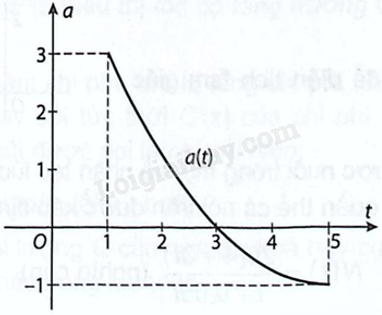
a) Lập bảng biến thiên của hàm vận tốc \(y = v\left( t \right)\) của vật, với \(t \in \left[ {1;5} \right]\).
b) Tại thời điểm nào vật chuyển động với vận tốc lớn nhất?
Phương pháp giải - Xem chi tiết
Ý a:
+ \(a\left( t \right) = v'\left( t \right)\). Từ đồ thị xét dấu \(a\left( t \right)\) trên khoảng \(t \in \left[ {1;5} \right]\)
+ Lập bảng biến thiên của \(v\left( t \right)\).
Ý b: Từ bảng biến thiên suy ra được giá trị lớn nhất của vận tốc đạt được tại thời điểm nào.
Lời giải chi tiết
a) Ta có \(a\left( t \right) = v'\left( t \right)\).
Từ đồ thị ta có \(a\left( t \right) = 0 \Leftrightarrow t = 3\).
Ta thấy \(a\left( t \right) > 0\) với mọi \(t \in \left( {1;3} \right)\), \(a\left( t \right) < 0\) với mọi \(t \in \left( {3;5} \right)\).
Lập bảng biến thiên
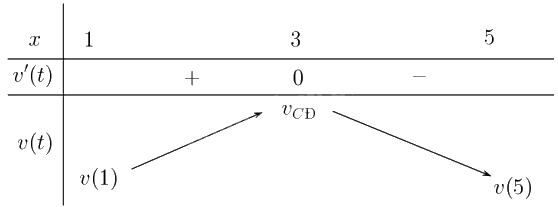
b) Từ bảng biến thiên suy ra vận tốc lớn nhất đạt tại giây thứ \(3\) (\(t = 3\)).
Giải bài 1.35 trang 25 SBT Toán 12 - Kết nối tri thức: Tổng quan
Bài 1.35 trang 25 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tiếp tuyến của đồ thị hàm số, cực trị của hàm số, hoặc các bài toán ứng dụng khác.
Nội dung bài 1.35 trang 25 SBT Toán 12 - Kết nối tri thức
Thông thường, bài 1.35 sẽ bao gồm một hoặc nhiều câu hỏi nhỏ, yêu cầu học sinh:
- Xác định đạo hàm của hàm số cho trước.
- Tìm các điểm cực trị của hàm số.
- Viết phương trình tiếp tuyến của đồ thị hàm số tại một điểm cho trước.
- Giải các bài toán tối ưu hóa liên quan đến hàm số.
Phương pháp giải bài 1.35 trang 25 SBT Toán 12 - Kết nối tri thức
Để giải quyết bài 1.35 một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Đạo hàm: Hiểu rõ các quy tắc tính đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
- Ứng dụng của đạo hàm: Nắm vững các ứng dụng của đạo hàm trong việc tìm cực trị của hàm số, xét tính đơn điệu của hàm số, và viết phương trình tiếp tuyến.
- Kỹ năng giải toán: Rèn luyện kỹ năng biến đổi đại số, giải phương trình, và vẽ đồ thị hàm số.
Lời giải chi tiết bài 1.35 trang 25 SBT Toán 12 - Kết nối tri thức
(Giả sử bài 1.35 có nội dung cụ thể như sau: Tìm đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1)
Lời giải:
Để tìm đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1, ta áp dụng quy tắc tính đạo hàm của tổng và hiệu, cũng như quy tắc tính đạo hàm của lũy thừa:
f'(x) = (x3)' - (3x2)' + (2x)' - (1)'
f'(x) = 3x2 - 6x + 2 - 0
f'(x) = 3x2 - 6x + 2
Vậy, đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1 là f'(x) = 3x2 - 6x + 2.
Lưu ý khi giải bài 1.35 trang 25 SBT Toán 12 - Kết nối tri thức
- Đọc kỹ đề bài để xác định yêu cầu của bài toán.
- Sử dụng đúng các công thức và quy tắc đạo hàm.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
- Nếu gặp khó khăn, hãy tham khảo các tài liệu học tập hoặc tìm kiếm sự giúp đỡ từ giáo viên và bạn bè.
Các bài tập tương tự
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, bạn có thể tham khảo các bài tập tương tự trong sách bài tập Toán 12 Kết nối tri thức, hoặc trên các trang web học toán trực tuyến.
Kết luận
Bài 1.35 trang 25 SBT Toán 12 Kết nối tri thức là một bài tập quan trọng giúp bạn hiểu sâu hơn về đạo hàm và các ứng dụng của nó. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.