Giải bài 1.48 trang 32 Sách bài tập Toán 12 - Kết nối tri thức

Giải bài 1.48 trang 32 sách bài tập toán 12 - Kết nối tri thức

Giải bài 1.48 trang 32 SBT Toán 12 Kết nối tri thức

Chào mừng các em học sinh đến với lời giải chi tiết bài 1.48 trang 32 sách bài tập Toán 12 Kết nối tri thức. Bài tập này thuộc chương trình học Toán 12, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.

tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và các kiến thức bổ trợ cần thiết.

Một công ty ước tính rằng chi phí (C) (USD) để sản xuất (x) đơn vị sản phẩm có thể được mô hình hóa bằng công thức (C = 800 + 0,04x + 0,0002{x^2}). Tìm mức sản xuất sao cho chi phí trung bình (overline C left( x right) = frac{{Cleft( x right)}}{x}) cho mỗi đơn vị hàng hóa là nhỏ nhất.

Đề bài

Một công ty ước tính rằng chi phí \(C\) (USD) để sản xuất \(x\) đơn vị sản phẩm có thể được mô hình hóa bằng công thức

\(C = 800 + 0,04x + 0,0002{x^2}\).

Tìm mức sản xuất sao cho chi phí trung bình \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x}\) cho mỗi đơn vị hàng hóa là nhỏ nhất.

Phương pháp giải - Xem chi tiết Giải bài 1.48 trang 32 sách bài tập toán 12 - Kết nối tri thức 1

+ Viết công thức \(\overline C \left( x \right)\).

+ Tìm \(x > 0\) để \(\overline C \left( x \right)\) nhỏ nhất.

Lời giải chi tiết

Ta có \(\overline C \left( x \right) = \frac{{800 + 0,04x + 0,0002{x^2}}}{x} = \frac{{800}}{x} + 0,04 + 0,0002x\), \(x > 0\)

Chi phí trung bình nhỏ nhất khi \(\overline C \left( x \right)\) đạt giá trị nhỏ nhất, ta cần tìm \(x\) để \(\overline C \left( x \right)\) nhỏ nhất.

Ta có \(\overline {C'} \left( x \right) = \frac{{ - 800}}{{{x^2}}} + 0,0002 = \frac{{ - 800 + 0,0002{x^2}}}{{{x^2}}}\).

Khi đó \(\overline {C'} \left( x \right) = 0 \Leftrightarrow \frac{{ - 800 + 0,0002{x^2}}}{{{x^2}}} = 0 \Leftrightarrow - 800 + 0,0002{x^2} = 0 \Leftrightarrow x = 2000\) vì \(x > 0\).

Lập bảng biến thiên

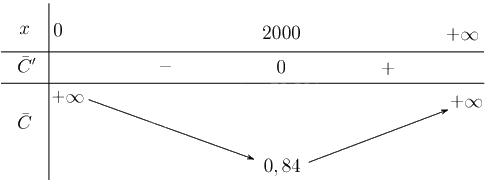
Giải bài 1.48 trang 32 sách bài tập toán 12 - Kết nối tri thức 2

Từ bảng biến thiên suy ra \(\overline C \left( x \right)\) đạt giá trị nhỏ nhất khi \(x = 2000\).

Vậy với mức sản xuất \(2000\) thì chi phí trung bình cho mỗi đơn vị hàng hóa là nhỏ nhất.

Giải bài 1.48 trang 32 SBT Toán 12 Kết nối tri thức: Tổng quan và Phương pháp giải

Bài 1.48 trang 32 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Để giải bài tập này một cách hiệu quả, các em cần nắm vững các khái niệm và công thức liên quan.

Nội dung bài tập 1.48 trang 32 SBT Toán 12 Kết nối tri thức

Bài tập yêu cầu học sinh tìm cực trị của hàm số. Cụ thể, bài tập thường cho một hàm số và yêu cầu xác định các điểm cực đại, cực tiểu của hàm số đó. Để làm được điều này, các em cần thực hiện các bước sau:

Tính đạo hàm bậc nhất (f'(x)) của hàm số.
Tìm các điểm dừng (x) bằng cách giải phương trình f'(x) = 0.
Xác định dấu của đạo hàm bậc nhất trên các khoảng xác định bởi các điểm dừng để xác định khoảng hàm số đồng biến, nghịch biến.
Sử dụng tiêu chuẩn xét cực trị (dấu của đạo hàm bậc nhất đổi dấu) để xác định các điểm cực đại, cực tiểu.
Tính giá trị của hàm số tại các điểm cực trị để tìm giá trị cực đại, cực tiểu.

Lời giải chi tiết bài 1.48 trang 32 SBT Toán 12 Kết nối tri thức

Để minh họa, chúng ta sẽ cùng giải một ví dụ cụ thể. Giả sử hàm số cần xét là f(x) = x³ - 3x² + 2.

Tính đạo hàm bậc nhất: f'(x) = 3x² - 6x
Tìm điểm dừng: 3x² - 6x = 0 => x = 0 hoặc x = 2
Xác định dấu của đạo hàm bậc nhất:
- Khi x < 0: f'(x) > 0 (hàm số đồng biến)
- Khi 0 < x < 2: f'(x) < 0 (hàm số nghịch biến)
- Khi x > 2: f'(x) > 0 (hàm số đồng biến)
Kết luận:
- Tại x = 0, f'(x) đổi dấu từ dương sang âm, nên x = 0 là điểm cực đại. Giá trị cực đại là f(0) = 2.
- Tại x = 2, f'(x) đổi dấu từ âm sang dương, nên x = 2 là điểm cực tiểu. Giá trị cực tiểu là f(2) = -2.

Mẹo giải nhanh và lưu ý quan trọng

Nắm vững các công thức đạo hàm cơ bản.
Chú ý kiểm tra điều kiện xác định của hàm số.
Sử dụng bảng xét dấu đạo hàm bậc nhất để xác định khoảng đồng biến, nghịch biến một cách chính xác.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Các bài tập tương tự và tài liệu tham khảo

Để luyện tập thêm, các em có thể tham khảo các bài tập tương tự trong sách bài tập Toán 12 Kết nối tri thức và các đề thi thử Toán 12. Ngoài ra, các em cũng có thể tìm kiếm các tài liệu tham khảo trực tuyến hoặc tham gia các khóa học luyện thi Toán 12 để nâng cao kiến thức và kỹ năng.

tusach.vn hy vọng rằng lời giải chi tiết bài 1.48 trang 32 SBT Toán 12 Kết nối tri thức này sẽ giúp các em hiểu rõ hơn về phương pháp giải và tự tin hơn trong quá trình học tập. Chúc các em học tốt!