Giải bài 1.61 trang 35 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 1.61 trang 35 SBT Toán 12 - Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết bài 1.61 trang 35 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác và đầy đủ nhất, đồng thời giải thích rõ ràng từng bước để bạn có thể hiểu sâu sắc về bài toán.
Cho hàm số (y = frac{{ax + b}}{{cx + d}}) có đồ thị như hình vẽ sau: Mệnh đề nào sau đây là mệnh đề đúng? A. (bc < ad < 0). B. (ad < 0 < bc). C. (0 < ad < bc). D. (ad < bc < 0).
Đề bài
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như hình vẽ sau:
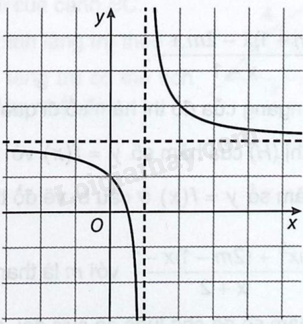
Mệnh đề nào sau đây là mệnh đề đúng?
A. \(bc < ad < 0\)
B. \(ad < 0 < bc\)
C. \(0 < ad < bc\)
D. \(ad < bc < 0\)
Phương pháp giải - Xem chi tiết
Quan sát đồ thị và tính đạo hàm, nhận xét về sự biến thiên, tiệm cận, giao điểm với hai trục tọa độ của đồ thị hàm số.
Lời giải chi tiết
Đáp án: D.
Ta có \(y' = \frac{{ad - bc}}{{cx + d}}\). Từ đồ thị ta thấy hàm số nghịch biến trên tập xác định của nó.
Suy ra \(y' < 0 \Leftrightarrow \frac{{ad - bc}}{{cx + d}} < 0 \Leftrightarrow ad - bc < 0 \Leftrightarrow ad < bc\). Từ đó ta loại đáp án A.
Quan sát ba đáp án còn lại, ta cần tìm dấu của \(ad\) và \(bc\) để chọn được đáp án đúng (so sánh với 0).
Xét giao điểm của đồ thị với các trục:
+ Trục hoành: giao điểm là \(\left( {\frac{{ - b}}{a};0} \right)\) có hoành độ dương suy ra \(\frac{{ - b}}{a} > 0 \Leftrightarrow ab < 0\). Do đó \(a\) và \(b\) trái dấu.
+ Trục tung: giao điểm là \(\left( {0;\frac{b}{d}} \right)\) có tung độ dương suy ra \(\frac{b}{d} > 0 \Leftrightarrow bd > 0\). Do đó \(b\) và \(d\) cùng dấu.
Suy ra \(a\) và \(d\) trái dấu hay \(ad < 0\). Do đó ta loại tiếp đáp án C.
Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = \frac{{ax + b}}{{cx + d}} = \frac{a}{c}\) suy ra đồ thị có tiệm cận ngang là đường thẳng \(y = \frac{a}{c}\).
Mà tiệm cận ngang là đường thẳng nằm phía trên trục hoành (quan sát hình vẽ), nên \(\frac{a}{c} > 0 \Leftrightarrow ac > 0\).
Hay \(a\) và \(c\) cùng dấu. Vì \(a\) và \(b\) trái dấu (đã chứng minh) nên \(c\)và \(b\) trái dấu hay \(bc < 0\), ta loại đáp án B.
Vậy ta chọn đáp án D.
Giải bài 1.61 trang 35 SBT Toán 12 - Kết nối tri thức: Phân tích và Lời giải Chi Tiết
Bài 1.61 trang 35 sách bài tập Toán 12 Kết nối tri thức là một bài tập thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và công thức liên quan đến đạo hàm, đồng thời rèn luyện kỹ năng giải toán một cách thành thạo.
Nội dung bài tập 1.61 trang 35 SBT Toán 12 - Kết nối tri thức
Bài 1.61 yêu cầu học sinh giải quyết một bài toán liên quan đến việc tìm đạo hàm của hàm số và ứng dụng đạo hàm để giải quyết các bài toán tối ưu hóa. Cụ thể, bài tập có thể yêu cầu:
- Tìm đạo hàm của một hàm số cho trước.
- Xác định các điểm cực trị của hàm số.
- Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
- Giải các bài toán tối ưu hóa liên quan đến việc tìm kích thước tối ưu của một vật thể hoặc tìm chi phí tối thiểu để sản xuất một sản phẩm.
Lời giải chi tiết bài 1.61 trang 35 SBT Toán 12 - Kết nối tri thức
Để giải bài 1.61 trang 35 SBT Toán 12 - Kết nối tri thức, chúng ta thực hiện các bước sau:
- Bước 1: Xác định hàm số cần tìm đạo hàm.
- Bước 2: Sử dụng các quy tắc đạo hàm để tìm đạo hàm của hàm số.
- Bước 3: Giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị của hàm số.
- Bước 4: Sử dụng các tiêu chuẩn xét dấu đạo hàm để xác định loại điểm cực trị (cực đại hoặc cực tiểu).
- Bước 5: Tính giá trị của hàm số tại các điểm cực trị và các điểm đầu mút của khoảng xét dấu để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
Ví dụ minh họa: (Giả sử bài tập cụ thể là tìm giá trị lớn nhất của hàm số f(x) = -x2 + 4x - 3 trên khoảng [0; 3])
Lời giải:
- f'(x) = -2x + 4
- Giải f'(x) = 0, ta được x = 2
- f(0) = -3
- f(2) = 1
- f(3) = 0
- Vậy giá trị lớn nhất của hàm số trên khoảng [0; 3] là 1, đạt được tại x = 2.
Mẹo giải bài tập đạo hàm hiệu quả
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:
- Nắm vững các quy tắc đạo hàm cơ bản.
- Rèn luyện kỹ năng giải toán thường xuyên.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm giải toán.
- Tham khảo các tài liệu học tập và bài giảng trên mạng.
Các bài tập tương tự và tài liệu tham khảo
Ngoài bài 1.61 trang 35, bạn có thể tham khảo các bài tập tương tự trong sách bài tập Toán 12 Kết nối tri thức để rèn luyện thêm kỹ năng giải toán. Bạn cũng có thể tìm kiếm các tài liệu tham khảo trên mạng hoặc tại các thư viện để học hỏi thêm kiến thức về đạo hàm.
Tusach.vn hy vọng rằng lời giải chi tiết bài 1.61 trang 35 SBT Toán 12 - Kết nối tri thức này sẽ giúp bạn hiểu rõ hơn về đạo hàm và tự tin làm bài tập. Chúc bạn học tập tốt!