Giải bài 4.24 trang 17 SBT Toán 12 - Kết nối tri thức

Giải bài 4.24 trang 17 sách bài tập toán 12 - Kết nối tri thức

Giải bài 4.24 trang 17 SBT Toán 12 Kết nối tri thức

Chào mừng bạn đến với lời giải chi tiết bài 4.24 trang 17 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài tập.

Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ quá trình học tập của bạn. Hãy cùng tusach.vn khám phá lời giải chi tiết ngay sau đây!

Tính thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh (Ox): a) (y = 2sqrt x ,{rm{ y}} = 0,{rm{ }}x = 1,{rm{ }}x = 4); b) (y = 4x,{rm{ }}y = {x^3},{rm{ }}x = 0,{rm{ }}x = 2).

Đề bài

Tính thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh \(Ox\):

a) \(y = 2\sqrt x ,{\rm{ y}} = 0,{\rm{ }}x = 1,{\rm{ }}x = 4\);

b) \(y = 4x,{\rm{ }}y = {x^3},{\rm{ }}x = 0,{\rm{ }}x = 2\).

Phương pháp giải - Xem chi tiết Giải bài 4.24 trang 17 sách bài tập toán 12 - Kết nối tri thức 1

Ý a: Sử dụng trực tiếp công thức tính thể tích khối tròn xoay .

Ý b: Tính lần lượt thể tích khi quay hình phẳng giới hạn bởi các đường \(y = 4x,{\rm{ }}y = 0,\)\({\rm{ }}x = 0,\) \(x = 2\) quanh trục Ox và thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường \(y = {x^3},{\rm{ }}y = 0,{\rm{ }}x = 0,{\rm{ }}x = 2\) quanh trục Ox. Lấy hiệu hai thể tích vừa tính ta tìm được thể tích theo yêu cầu, tuy nhiên ta cần xác định xem lấy thể tích nào trừ thể tích còn lại phụ thuộc vào các đồ thị.

Lời giải chi tiết

a) Thể tích cần tìm là \(V = \pi \int\limits_1^4 {{{\left( {2\sqrt x } \right)}^2}dx} = \pi \int\limits_1^4 {4xdx} = 2\pi \left. {{x^2}} \right|_1^4 = 32\pi - 2\pi = 30\pi \).

b) Ta có hình vẽ biểu hình phẳng cần tính diện tích như bên dưới.

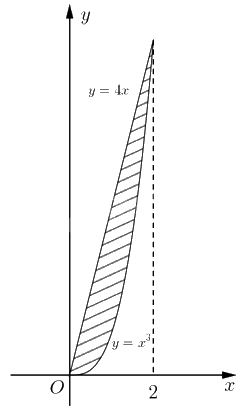
Giải bài 4.24 trang 17 sách bài tập toán 12 - Kết nối tri thức 2

Ta thấy đồ thị của hàm số \(y = 4x\) nằm phía trên đồ thị \(y = {x^3}\). Do đó thể tích cần tìm sẽ bằng thể tích khối tròn

xoay khi quay hình phẳng giới hạn bởi các đường \(y = 4x,{\rm{ }}y = 0,{\rm{ }}x = 0,{\rm{ }}x = 2\) quanh trục Ox (gọi là \({V_1}\) ) trừ đi thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường \(y = {x^3},{\rm{ }}y = 0,{\rm{ }}x = 0,{\rm{ }}x = 2\) quanh trục Ox (gọi là \({V_2}\)).

Ta có \({V_1} = \pi \int\limits_0^2 {{{\left( {4x} \right)}^2}dx} \) và \({V_2} = \pi \int\limits_0^2 {{{\left( {{x^3}} \right)}^2}dx} \).

Do đó thể tích cần tìm là

\(V = {V_1} - {V_2} = \pi \int\limits_0^2 {{{\left( {4x} \right)}^2}dx} - \pi \int\limits_0^2 {{{\left( {{x^3}} \right)}^2}dx} = \pi \int\limits_0^2 {\left( {16{x^2} - {x^6}} \right)dx} \)\( = \pi \left. {\left( {\frac{{16}}{3}{x^3} - \frac{{{x^7}}}{7}} \right)} \right|_0^2 = \frac{{512\pi }}{{21}}\).

Giải bài 4.24 trang 17 SBT Toán 12 Kết nối tri thức: Tổng quan và Phương pháp

Bài 4.24 trang 17 sách bài tập Toán 12 Kết nối tri thức thường xoay quanh các chủ đề về đạo hàm, ứng dụng của đạo hàm trong việc khảo sát hàm số, hoặc các bài toán liên quan đến hình học giải tích. Để giải quyết bài toán này một cách hiệu quả, bạn cần nắm vững các kiến thức cơ bản sau:

Đạo hàm: Định nghĩa, các quy tắc tính đạo hàm của các hàm số cơ bản (đa thức, lượng giác, mũ, logarit).
Ứng dụng của đạo hàm: Khảo sát hàm số (xác định khoảng đồng biến, nghịch biến, cực trị), giải phương trình, bất phương trình.
Hình học giải tích: Phương trình đường thẳng, đường tròn, elip, hypebol, parabol.

Lời giải chi tiết bài 4.24 trang 17 SBT Toán 12 Kết nối tri thức

(Giả sử bài 4.24 là một bài toán về khảo sát hàm số. Nội dung lời giải sẽ được trình bày chi tiết như sau. Đây chỉ là ví dụ, cần thay thế bằng lời giải chính xác của bài toán.)

Đề bài: Khảo sát hàm số y = x³ - 3x² + 2.

Xác định tập xác định: Hàm số y = x³ - 3x² + 2 xác định trên R.
Tính đạo hàm cấp nhất: y' = 3x² - 6x.
Tìm điểm dừng: y' = 0 ⇔ 3x² - 6x = 0 ⇔ x(3x - 6) = 0 ⇔ x = 0 hoặc x = 2.
Lập bảng biến thiên:
x -∞ 0 2 +∞
y' + 0 - +
y ↗ 2 ↘ -2 ↗
Kết luận: Hàm số đồng biến trên khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.

x	-∞	0	2	+∞
y'	+	0	-	+
y	↗	2	↘	-2	↗

Mẹo giải bài tập Toán 12 hiệu quả

Để học tốt môn Toán 12 và giải quyết các bài tập một cách nhanh chóng, bạn có thể áp dụng một số mẹo sau:

Nắm vững kiến thức cơ bản: Đây là nền tảng quan trọng nhất để giải quyết mọi bài toán.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp bạn hiểu sâu hơn về kiến thức và rèn luyện kỹ năng giải toán.
Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm vẽ đồ thị, các trang web giải toán trực tuyến có thể giúp bạn tiết kiệm thời gian và công sức.
Học hỏi từ bạn bè và thầy cô: Trao đổi kiến thức, kinh nghiệm với bạn bè và thầy cô sẽ giúp bạn mở rộng tầm nhìn và tìm ra những phương pháp giải toán mới.

Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục Toán học

Tusach.vn là website cung cấp lời giải bài tập Toán 12 Kết nối tri thức và các môn học khác một cách nhanh chóng, chính xác và dễ hiểu. Chúng tôi luôn cập nhật nội dung mới nhất và cung cấp các bài giảng chất lượng cao để giúp bạn học tập hiệu quả. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!