Giải bài 1.3 trang 9 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 1.3 trang 9 sách bài tập Toán 12 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 1.3 trang 9 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải chi tiết để giúp các em nắm vững kiến thức và tự tin làm bài tập.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau: a) (y = x + frac{1}{x}); b) (y = frac{x}{{{x^2} + 1}}).
Đề bài
Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau:
a) \(y = x + \frac{1}{x}\);
b) \(y = \frac{x}{{{x^2} + 1}}\).
Phương pháp giải - Xem chi tiết
Ý a:
- Tìm tập xác định của hàm số.
- Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng \(0\) hoặc đạo hàm không tồn tại.
- Lập bảng biến thiên của hàm số.
- Từ bảng biến thiên suy ra các khoảng đồng biến, nghịch biến, cực trị của hàm số.
Ý b:
- Tìm tập xác định của hàm số.
- Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng \(0\).
- Lập bảng biến thiên của hàm số.
- Từ bảng biến thiên suy ra các khoảng đồng biến, nghịch biến, cực trị của hàm số.
Lời giải chi tiết
a) Tập xác định: \(\mathbb{R}\backslash \left\{ 0 \right\}\)
Ta có \(y' = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}}\). Khi đó \(y' = 0 \Leftrightarrow \frac{{{x^2} - 1}}{{{x^2}}} = 0 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow x = - 1\) hoặc \(x = 1\).
Lập bảng biến thiên của hàm số:
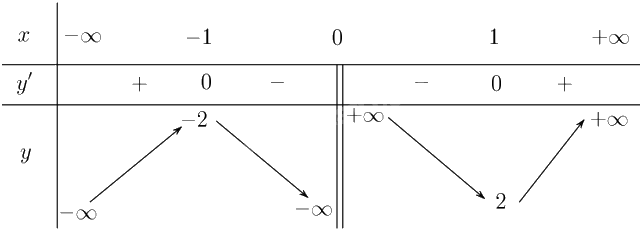
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\).
Hàm số đạt cực đại tại \(x = - 1\) và \({y_{CĐ}} = y\left( -1 \right) = -2\).
Hàm số đạt cực tiểu tại \(x = 1\) và \({y_{CT}} = y\left( 1 \right) = 2\).
b) Tập xác định: \(\mathbb{R}\)
Ta có \(y' = \frac{{1 \cdot \left( {{x^2} + 1} \right) - x \cdot 2x}}{{{{\left( {{x^2} + 1} \right)}^2}}} = \frac{{ - {x^2} + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}}\).
Khi đó \(y' = 0 \Leftrightarrow \frac{{ - {x^2} + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}} = 0 \Leftrightarrow - {x^2} + 1 = 0 \Leftrightarrow x = - 1\) hoặc \(x = 1\).
Lập bảng biến thiên của hàm số:
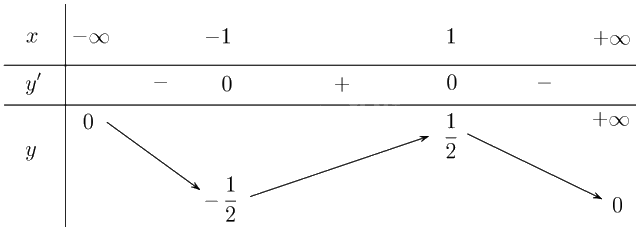
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên khoảng \(\left( { - 1;1} \right)\).
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số đạt cực đại tại \(x = 1\) và \({y_{CĐ}} = y\left( { - 1} \right) = \frac{1}{2}\).
Hàm số đạt cực tiểu tại \(x = - 1\) và \({y_{CT}} = y\left( { - 1} \right) = - \frac{1}{2}\).
Giải bài 1.3 trang 9 SBT Toán 12 - Kết nối tri thức: Tổng quan
Bài 1.3 trang 9 sách bài tập Toán 12 Kết nối tri thức thuộc chương 1: Giới hạn. Dạng bài tập này thường tập trung vào việc tính giới hạn của hàm số tại một điểm, sử dụng các định nghĩa và tính chất của giới hạn. Việc nắm vững kiến thức về giới hạn là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 12.
Nội dung bài 1.3 trang 9 SBT Toán 12 - Kết nối tri thức
Bài 1.3 thường bao gồm các câu hỏi và bài tập sau:
- Tính giới hạn của hàm số khi x tiến tới một giá trị cụ thể.
- Sử dụng các định lý về giới hạn để đơn giản hóa biểu thức và tính giới hạn.
- Xác định xem một hàm số có giới hạn tại một điểm hay không.
- Ứng dụng giới hạn vào việc giải các bài toán thực tế.
Lời giải chi tiết bài 1.3 trang 9 SBT Toán 12 - Kết nối tri thức
Để giúp các em hiểu rõ hơn về cách giải bài 1.3 trang 9, chúng ta sẽ đi vào giải chi tiết từng câu hỏi:
Câu a: (Ví dụ minh họa - cần thay thế bằng nội dung thực tế của bài tập)
Giả sử câu a yêu cầu tính lim (x→2) (x2 - 4) / (x - 2)
- Phân tích tử số: x2 - 4 = (x - 2)(x + 2)
- Rút gọn biểu thức: (x2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2 (với x ≠ 2)
- Tính giới hạn: lim (x→2) (x + 2) = 2 + 2 = 4
- Vậy, lim (x→2) (x2 - 4) / (x - 2) = 4
Câu b: (Ví dụ minh họa - cần thay thế bằng nội dung thực tế của bài tập)
Giả sử câu b yêu cầu tính lim (x→∞) (2x + 1) / (x - 3)
- Chia cả tử và mẫu cho x: lim (x→∞) (2 + 1/x) / (1 - 3/x)
- Khi x→∞, 1/x → 0 và 3/x → 0
- Tính giới hạn: lim (x→∞) (2 + 0) / (1 - 0) = 2/1 = 2
- Vậy, lim (x→∞) (2x + 1) / (x - 3) = 2
Mẹo giải bài tập giới hạn Toán 12
Để giải tốt các bài tập về giới hạn, các em cần:
- Nắm vững các định nghĩa và tính chất của giới hạn.
- Thành thạo các phương pháp tính giới hạn như phân tích đa thức, chia cả tử và mẫu cho x, sử dụng các định lý giới hạn.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn cung cấp đầy đủ lời giải chi tiết các bài tập trong sách bài tập Toán 12 Kết nối tri thức, cùng với các tài liệu học tập hữu ích khác như lý thuyết, công thức, đề thi thử. Hãy truy cập tusach.vn để học tập hiệu quả và đạt kết quả cao trong môn Toán 12!
| Chương | Nội dung chính |
|---|---|
| 1 | Giới hạn |
| 2 | Hàm số liên tục |
| 3 | Đạo hàm |
| Đây chỉ là một phần nhỏ trong chương trình Toán 12. Hãy cùng Tusach.vn khám phá thêm nhiều kiến thức thú vị khác! | |