Giải bài 1.68 trang 37 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 1.68 trang 37 SBT Toán 12 Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết bài 1.68 trang 37 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác và đầy đủ nhất, đồng thời giải thích rõ ràng từng bước để bạn có thể hiểu sâu sắc về bài toán.
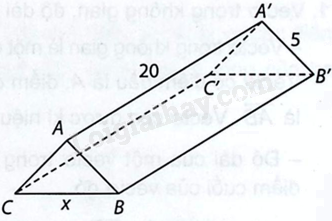
Một hành lang giữa hai nhà có hình dạng của một lăng trụ đứng (xem hình bên). Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20 m, rộng 5 m. Gọi x (m) là độ dài của cạnh BC. a) Tính thể tích V của hình lăng trụ theo x. b) Tìm x sao cho hình lăng trụ có thể tích lớn nhất và tính giá trị lớn nhất đó.
Đề bài
Một hành lang giữa hai nhà có hình dạng của một lăng trụ đứng (xem hình bên). Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20 m, rộng 5 m. Gọi x (m) là độ dài của cạnh BC.
a) Tính thể tích V của hình lăng trụ theo x.
b) Tìm x sao cho hình lăng trụ có thể tích lớn nhất và tính giá trị lớn nhất đó.
Phương pháp giải - Xem chi tiết
Ý a: Sử dụng một số kiến thức về hình học phẳng và hình lăng trụ để tìm được diện tích đáy và chiều cao, từ đó tính được thể tích V.
Ý b: Xét hàm số V theo x trên \(\left( {0;10} \right)\)sau đó lập bảng biến thiên và tìm giá trị lớn nhất của hàm số.
Lời giải chi tiết
a) Ta thấy do ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật có kích thước giống nhau nên \(AC = AB\) (đều là chiều rộng của mặt hình chữ nhật) do đó đáy \(ABC\)là tam giác cân tại
\(A\). Gọi \(H\) là trung điểm cạnh \(AB\) suy ra \(AH\) là đường cao của tam giác (tính chất tam giác cân). Ta có \(AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {25 - {{\left( {\frac{x}{2}} \right)}^2}} = \frac{1}{2}\sqrt {100 - {x^2}} \).
Diện tích tam giác ABC là \(S = \frac{1}{2}BC \cdot AH = \frac{1}{2}x \cdot \frac{1}{2}\sqrt {100 - {x^2}} = \frac{1}{4}x\sqrt {100 - {x^2}} \).
Thể tích khối lăng trụ là \(V = S \cdot AA' = 5x\sqrt {100 - {x^2}} \) (m3) với \(0 < x < 10\).
b) Xét hàm số \(V = 5x\sqrt {100 - {x^2}} \) trên \(\left( {0;10} \right)\).
Ta có \(V' = 5x\sqrt {100 - {x^2}} + 5x\frac{{ - 2x}}{{2\sqrt {100 - {x^2}} }} = \frac{{500 - 10{x^2}}}{{\sqrt {100 - {x^2}} }};\)
Suy ra \(V' = 0 \Leftrightarrow 500 - 10{x^2} = 0 \Leftrightarrow x = 5\sqrt 2 \) do \(x > 0\).
Lập bảng biến thiên:
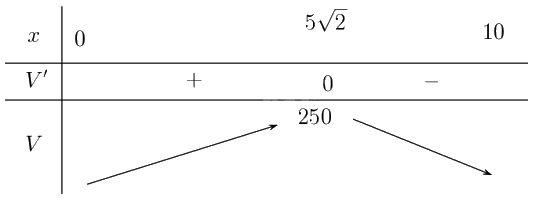
Vậy hình lăng trụ có thể tích lớn nhất khi \(x = 5\sqrt 2 \) (m). \(\mathop {\max }\limits_{\left( {0;10} \right)} V = V\left( {5\sqrt 2 } \right) = 250\) (m3).
Giải bài 1.68 trang 37 SBT Toán 12 Kết nối tri thức: Tổng quan
Bài 1.68 trang 37 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Cụ thể, bài toán thường liên quan đến việc tìm đạo hàm, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số, hoặc tìm cực trị của hàm số.
Nội dung bài 1.68 trang 37 SBT Toán 12 Kết nối tri thức
Để giải quyết bài 1.68 trang 37 SBT Toán 12 Kết nối tri thức, bạn cần thực hiện các bước sau:
- Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần xét.
- Tính đạo hàm: Sử dụng các quy tắc tính đạo hàm đã học để tính đạo hàm của hàm số.
- Xét dấu đạo hàm: Tìm các điểm mà đạo hàm bằng 0 hoặc không xác định. Sau đó, xét dấu đạo hàm trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến của hàm số.
- Tìm cực trị: Dựa vào dấu của đạo hàm để xác định các điểm cực trị của hàm số (cực đại, cực tiểu).
- Kết luận: Viết kết luận về khoảng đồng biến, nghịch biến và cực trị của hàm số.
Lời giải chi tiết bài 1.68 trang 37 SBT Toán 12 Kết nối tri thức
(Giả sử bài toán cụ thể là: Tìm khoảng đồng biến, nghịch biến của hàm số y = x3 - 3x2 + 2)
Giải:
- Tính đạo hàm: y' = 3x2 - 6x
- Xét dấu đạo hàm:
- y' = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
- Bảng xét dấu:
x -∞ 0 2 +∞ y' + - + y Đồng biến Nghịch biến Đồng biến - Kết luận: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Mẹo giải bài tập đạo hàm Toán 12
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính cầm tay để kiểm tra lại kết quả.
- Đọc kỹ đề bài và xác định chính xác yêu cầu của bài toán.
Tài liệu tham khảo hữu ích
- Sách giáo khoa Toán 12 - Kết nối tri thức
- Sách bài tập Toán 12 - Kết nối tri thức
- Các trang web học Toán trực tuyến uy tín
Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về cách giải bài 1.68 trang 37 SBT Toán 12 Kết nối tri thức. Chúc bạn học tập tốt!