Giải bài 1.46 trang 32 Sách bài tập Toán 12 - Kết nối tri thức

Giải bài 1.46 trang 32 sách bài tập toán 12 - Kết nối tri thức

Giải bài 1.46 trang 32 SBT Toán 12 Kết nối tri thức

Chào mừng bạn đến với lời giải chi tiết bài 1.46 trang 32 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Chúng tôi luôn cố gắng cung cấp những lời giải chính xác và đầy đủ nhất, đồng thời giải thích rõ ràng từng bước để bạn có thể hiểu sâu sắc về bài toán.

Ở ({0^ circ }C), sự mất nhiệt (H) (tính bằng Kcal/m2h, ở đây Kcal là kilocalories và 1 Kcal=1000 calo) từ cơ thể của một người có thể được mô hình hóa bằng công thức (H = 33left( {10sqrt v - v + 10,45} right),) Trong đó (v) là tốc độ gió (tính bằng m/s) (Theo sách Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009). a) Xét tính đơn điệu của hàm số (H) và giải thích ý nghĩa thực tiễn của kết quả nhận được. b) Tìm tốc độ thay đổi của (H) khi (v = 2) m/

Đề bài

Ở \({0^ \circ }C\), sự mất nhiệt \(H\) (tính bằng Kcal/m²h, ở đây Kcal là kilocalories và 1 Kcal=1000 calo) từ cơ thể của một người có thể được mô hình hóa bằng công thức

\(H = 33\left( {10\sqrt v - v + 10,45} \right),\)

Trong đó \(v\) là tốc độ gió (tính bằng m/s) (Theo sách Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009).

a) Xét tính đơn điệu của hàm số \(H\) và giải thích ý nghĩa thực tiễn của kết quả nhận được.

b) Tìm tốc độ thay đổi của \(H\) khi \(v = 2\) m/s. Giải thích ý nghĩa thực tiễn của kết quả này.

Phương pháp giải - Xem chi tiết Giải bài 1.46 trang 32 sách bài tập toán 12 - Kết nối tri thức 1

Ý a: Xét sự biến thiên của hàm số \(H\left( v \right) = 33\left( {10\sqrt v - v + 10,45} \right)\), sau đó nhận xét về mối liên hệ giữa mức nhiệt mất từ cơ thể và tốc độ gió.

Ý b: Tính \(H'\left( 2 \right)\), giá trị này là mức nhiệt của cơ thể mất tiếp khi vận tốc gió tăng từ \(2\) m/s lên \(3\) m/s.

Lời giải chi tiết

a) Xét hàm số \(H\left( v \right) = 33\left( {10\sqrt v - v + 10,45} \right)\).

Ta có \(H'\left( v \right) = 33\left( {\frac{5}{{\sqrt v }} - 1} \right),{\rm{ v > }}0\). Khi đó \(H'\left( v \right) = 0 \Leftrightarrow 33\left( {\frac{5}{{\sqrt v }} - 1} \right) = 0 \Leftrightarrow v = 25\).

Lập bảng biến thiên:

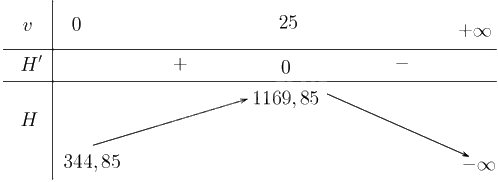
Giải bài 1.46 trang 32 sách bài tập toán 12 - Kết nối tri thức 2

Từ bảng biến thiên suy ra \(H\) đồng biến trên khoảng \(\left( {25; + \infty } \right)\), nghịch biến trên khoảng \(\left( {0;25} \right)\)

Do đó, mức nhiệt mất từ cơ thể tăng khi tốc độ gió tăng không vượt quá 25 m/s, đạt tối đa ở mức gió 25 m/s và sau đó giảm dần khi tốc độ gió tiếp tục tăng.

b) Ta có \(H'\left( 2 \right) = 33\left( {\frac{5}{{\sqrt 2 }} - 1} \right) \approx 83,673\).

Điều này có nghĩa là mức nhiệt của cơ thể mất tiếp khi vận tốc gió tăng từ \(2\) m/s lên \(3\) m/s là khoảng \(83,673\) (Kcal/m²h).

Giải bài 1.46 trang 32 SBT Toán 12 Kết nối tri thức: Tổng quan

Bài 1.46 trang 32 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tính đơn điệu, cực trị của hàm số, hoặc các bài toán ứng dụng thực tế.

Nội dung bài 1.46 trang 32 SBT Toán 12 Kết nối tri thức

Thông thường, bài 1.46 sẽ bao gồm một hoặc nhiều câu hỏi nhỏ, yêu cầu học sinh:

Tính đạo hàm của hàm số cho trước.
Xác định khoảng đơn điệu của hàm số.
Tìm cực trị của hàm số.
Giải các bài toán liên quan đến ứng dụng đạo hàm (ví dụ: tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước).

Lời giải chi tiết bài 1.46 trang 32 SBT Toán 12 Kết nối tri thức

Để giải bài 1.46 trang 32 SBT Toán 12 Kết nối tri thức một cách hiệu quả, bạn cần:

Nắm vững kiến thức cơ bản về đạo hàm: Hiểu rõ các công thức tính đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
Vận dụng linh hoạt các quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
Phân tích đề bài một cách cẩn thận: Xác định rõ yêu cầu của bài toán, các dữ kiện đã cho và các điều kiện ràng buộc.
Sử dụng các phương pháp giải phù hợp: Tùy thuộc vào từng dạng bài, bạn có thể sử dụng các phương pháp giải khác nhau (ví dụ: phương pháp xét dấu đạo hàm, phương pháp tìm điểm cực trị).

Ví dụ minh họa (giả định):

Giả sử bài 1.46 yêu cầu tìm cực trị của hàm số y = x³ - 3x² + 2.

Lời giải:

Tính đạo hàm: y' = 3x² - 6x
Tìm điểm cực trị: Giải phương trình y' = 0 => 3x² - 6x = 0 => x = 0 hoặc x = 2
Xác định loại cực trị: Xét dấu đạo hàm y' trên các khoảng (-∞; 0), (0; 2), (2; +∞).
Kết luận: Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.

Mẹo giải bài tập đạo hàm Toán 12

Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải.
Sử dụng máy tính bỏ túi: Máy tính bỏ túi có thể giúp bạn tính toán nhanh chóng và chính xác.
Tham khảo các tài liệu học tập: Sách giáo khoa, sách bài tập, các trang web học tập trực tuyến.
Hỏi thầy cô giáo hoặc bạn bè: Nếu bạn gặp khó khăn trong quá trình giải bài tập, đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè để được giúp đỡ.

Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín

Tusach.vn là một trang web cung cấp đầy đủ các tài liệu học tập Toán 12, bao gồm:

Lời giải chi tiết sách giáo khoa
Lời giải chi tiết sách bài tập
Các bài giảng video
Các bài kiểm tra trực tuyến

Hãy truy cập tusach.vn để học tập Toán 12 một cách hiệu quả nhất!