Giải bài 3 trang 48 SBT Toán 12 - Kết nối tri thức

Giải bài 3 trang 48 sách bài tập toán 12 - Kết nối tri thức

Giải bài 3 trang 48 sách bài tập Toán 12 - Kết nối tri thức

Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 48 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án, hướng dẫn giải chi tiết và phân tích từng bước để giúp các em hiểu rõ hơn về nội dung bài học.

Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.

Đồ thị trong hình vẽ dưới đây là của hàm số nào? A. (y = frac{{{x^2} - 2x}}{{x + 1}}). B. (y = frac{{{x^2} + 2x}}{{x + 1}}). C. (y = frac{{{x^2} + 2x + 2}}{{x + 1}}). D. (y = frac{{2x}}{{x + 1}}).

Đề bài

Đồ thị trong hình vẽ dưới đây là của hàm số nào?

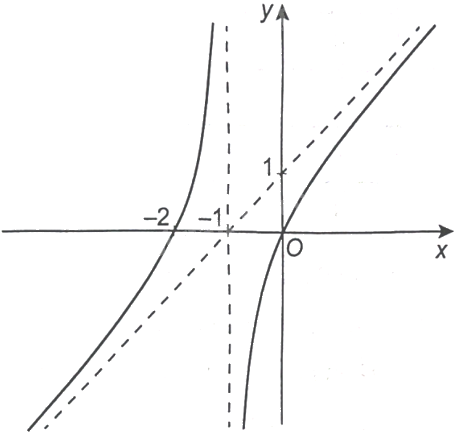
Giải bài 3 trang 48 sách bài tập toán 12 - Kết nối tri thức 1

A. \(y = \frac{{{x^2} - 2x}}{{x + 1}}\).

B. \(y = \frac{{{x^2} + 2x}}{{x + 1}}\).

C. \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\).

D. \(y = \frac{{2x}}{{x + 1}}\).

Phương pháp giải - Xem chi tiết Giải bài 3 trang 48 sách bài tập toán 12 - Kết nối tri thức 2

Tìm các tiệm cận đứng, xiên, ngang của đồ thị. Xét các điểm thuộc đồ thị có tọa độ cho sẵn trên hình.

Lời giải chi tiết

Từ hình vẽ ta thấy đồ thị có tiệm cận đứng \(x = - 1\), tiệm cận xiên \(y = x + 1\) và không có tiệm cận ngang. Ngoài ra đồ thị còn đi qua hai điểm \(O\left( {0;0} \right)\) và \(\left( { - 2;0} \right)\). Ta sẽ xét mỗi đồ thị trong từng đáp án.

Xét A:

\(y = \frac{{{x^2} - 2x}}{{x + 1}} = x - 3 + \frac{3}{{x + 1}}\) suy ra đồ thị có tiệm cận xiên \(y = x - 3\). Loại.

Xét B:

\(y = \frac{{{x^2} + 2x}}{{x + 1}} = x + 1 - \frac{1}{{x + 1}}\) suy ra đồ thị có tiệm cận xiên \(y = x + 1\) và tiệm cận đứng \(x = - 1\), ngoài ra đồ thị đi qua các điểm \(O\left( {0;0} \right)\) và \(\left( { - 2;0} \right)\). Do đó đồ thị thỏa mãn các điều kiện đang xét, tuy nhiên ta sẽ kiểm tra tiếp hai đáp án còn lại sau đó sẽ kết luận.

Xét C:

\(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) không đi qua điểm \(O\left( {0;0} \right)\). Loại.

Xét D:

\(y = \frac{{2x}}{{x + 1}}\) không đi qua điểm \(\left( { - 2;0} \right)\). Loại.

Đáp án B.

Giải bài 3 trang 48 SBT Toán 12 - Kết nối tri thức: Tổng quan và Hướng dẫn chi tiết

Bài 3 trang 48 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của tổng, hiệu, tích, thương và hàm hợp. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để giải quyết các bài toán liên quan đến cực trị, điểm uốn và ứng dụng của đạo hàm trong các lĩnh vực khác.

Nội dung bài 3 trang 48 SBT Toán 12 - Kết nối tri thức

Bài 3 bao gồm các câu hỏi và bài tập yêu cầu học sinh:

Tính đạo hàm của các hàm số cho trước.
Áp dụng quy tắc đạo hàm để giải các bài toán thực tế.
Phân tích và đánh giá kết quả tính đạo hàm.

Lời giải chi tiết bài 3 trang 48 SBT Toán 12 - Kết nối tri thức

Câu a)

Để giải câu a, ta sử dụng quy tắc đạo hàm của tổng và đạo hàm của hàm số mũ. Cụ thể:

f'(x) = (x^2 + 1)' + (e^x)' = 2x + e^x

Câu b)

Đối với câu b, ta áp dụng quy tắc đạo hàm của tích và đạo hàm của hàm số lượng giác:

g'(x) = (sin x)' * (x + 1) + sin x * (x + 1)' = cos x * (x + 1) + sin x * 1 = (x + 1)cos x + sin x

Câu c)

Câu c yêu cầu sử dụng quy tắc đạo hàm của thương:

h'(x) = [(x^2 - 1)' * (x + 2) - (x^2 - 1) * (x + 2)'] / (x + 2)^2 = [2x * (x + 2) - (x^2 - 1) * 1] / (x + 2)^2 = (x^2 + 4x + 1) / (x + 2)^2

Mẹo giải bài tập đạo hàm hiệu quả

Nắm vững các quy tắc đạo hàm cơ bản: Đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit.
Thành thạo quy tắc đạo hàm của hàm hợp: Đây là quy tắc quan trọng và thường xuyên được sử dụng trong các bài toán đạo hàm.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải toán.
Kiểm tra lại kết quả: Sau khi tính đạo hàm, hãy kiểm tra lại kết quả bằng cách thay các giá trị cụ thể của x vào hàm số và đạo hàm để đảm bảo tính chính xác.

Ứng dụng của đạo hàm trong thực tế

Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:

Tính vận tốc và gia tốc: Trong vật lý, đạo hàm của quãng đường theo thời gian là vận tốc, và đạo hàm của vận tốc theo thời gian là gia tốc.
Tìm cực trị của hàm số: Đạo hàm được sử dụng để tìm các điểm cực đại và cực tiểu của hàm số, giúp xác định giá trị lớn nhất và nhỏ nhất của hàm số trong một khoảng nhất định.
Tối ưu hóa: Đạo hàm được sử dụng để tối ưu hóa các bài toán kinh tế, kỹ thuật và khoa học.

Kết luận

Hy vọng với lời giải chi tiết và hướng dẫn giải bài 3 trang 48 sách bài tập Toán 12 Kết nối tri thức này, các em học sinh sẽ hiểu rõ hơn về nội dung bài học và tự tin giải quyết các bài tập tương tự. Hãy tiếp tục luyện tập và khám phá thêm nhiều kiến thức thú vị khác cùng Tusach.vn!