Giải bài 4.25 trang 17 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 4.25 trang 17 SBT Toán 12 - Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết bài 4.25 trang 17 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
Xét hình phẳng giới hạn bởi các đường (y = sqrt x ,y = frac{{{x^2}}}{8},x = 0,x = 4). a) Tính diện tích hình phẳng; b) Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng xung quanh trục Ox.
Đề bài
Xét hình phẳng giới hạn bởi các đường \(y = \sqrt x ,y = \frac{{{x^2}}}{8},x = 0,x = 4\).
a) Tính diện tích hình phẳng;
b) Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng xung quanh trục Ox.
Phương pháp giải - Xem chi tiết
Ý a: Xác định xem hàm số nào có đồ thị nằm phía trên với \(x \in \left[ {0;4} \right]\). Sử dụng trực tiếp công thức tính diện tích.
Ý b: Tính lần lượt thể tích khi quay hình phẳng giới hạn bởi các đường \(y = \sqrt x ,y = 0,x = 0,x = 4\)quanh trục Ox và thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi các đường \(y = \frac{{{x^2}}}{8},y = 0,x = 0,x = 4\) quanh trục Ox. Lấy hiệu hai thể tích vừa tính ta tìm được thể thể tích theo yêu cầu, tuy nhiên ta cần xác định xem lấy thể tích nào trừ thể tích còn lại phụ thuộc vào các đồ thị.
Lời giải chi tiết
a) Ta có hình biểu diễn diện tích hình phẳng cần tìm như sau:
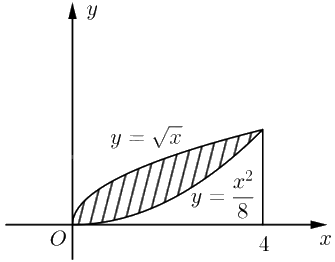
Ta thấy đồ thị \(y = \sqrt x \) nằm phía trên \(y = \frac{{{x^2}}}{8}\).
Diện tích cần tìm là \(S = \int\limits_0^4 {\left( {\sqrt x - \frac{{{x^2}}}{8}} \right)dx} = \left. {\left( {\frac{2}{3}x\sqrt x - \frac{{{x^3}}}{{24}}} \right)} \right|_0^4 = \frac{8}{3}\).
b) Thể tích khi xoay các đường \(y = \sqrt x ,y = 0,x = 0,x = 4\) quanh trục Ox là
\({V_1} = \pi \int\limits_0^4 {{{\left( {\sqrt x } \right)}^2}dx} = \pi \left. {\frac{{{x^2}}}{2}} \right|_0^4 = 8\pi \).
Thể tích khi xoay các đường \(y = \frac{{{x^2}}}{8},y = 0,x = 0,x = 4\) quanh trục Ox là
\({V_2} = \pi \int\limits_0^4 {{{\left( {\frac{{{x^2}}}{8}} \right)}^2}dx} = \pi \left. {\frac{{{x^5}}}{{320}}} \right|_0^4 = \frac{{16}}{5}\pi \).
Thể tích cần tìm là \(V = {V_1} - {V_2} = 8\pi - \frac{{16}}{5}\pi = \frac{{24}}{5}\pi \).
Giải bài 4.25 trang 17 SBT Toán 12 - Kết nối tri thức: Tổng quan và Phương pháp
Bài 4.25 trang 17 sách bài tập Toán 12 Kết nối tri thức thường thuộc chủ đề về đạo hàm, ứng dụng đạo hàm để khảo sát hàm số, hoặc các bài toán liên quan đến hình học giải tích. Để giải quyết bài toán này một cách hiệu quả, bạn cần nắm vững các kiến thức cơ bản sau:
- Kiến thức về đạo hàm: Cách tính đạo hàm của các hàm số cơ bản, quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Ứng dụng đạo hàm: Tìm cực trị của hàm số, xét tính đơn điệu của hàm số, giải phương trình, bất phương trình.
- Hình học giải tích: Phương trình đường thẳng, phương trình đường tròn, khoảng cách giữa hai điểm, giữa điểm và đường thẳng.
Lời giải chi tiết bài 4.25 trang 17 SBT Toán 12 - Kết nối tri thức
(Ở đây sẽ là lời giải chi tiết của bài 4.25. Vì không có nội dung cụ thể của bài toán, tôi sẽ đưa ra một ví dụ minh họa về cách trình bày lời giải.)
Ví dụ: Giả sử bài 4.25 yêu cầu tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.
- Tính đạo hàm: f'(x) = 3x2 - 6x
- Tìm điểm cực trị: Giải phương trình f'(x) = 0, ta được x = 0 hoặc x = 2.
- Xác định loại cực trị:
- Với x < 0, f'(x) > 0, hàm số đồng biến.
- Với 0 < x < 2, f'(x) < 0, hàm số nghịch biến.
- Với x > 2, f'(x) > 0, hàm số đồng biến.
Mở rộng và Bài tập tương tự
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong sách bài tập Toán 12 Kết nối tri thức. Hãy chú ý đến việc áp dụng đúng các công thức và quy tắc đạo hàm, cũng như phân tích kỹ đề bài để tìm ra phương pháp giải phù hợp.
Ngoài ra, bạn có thể tham khảo thêm các tài liệu học tập trực tuyến, video bài giảng, hoặc tìm kiếm sự giúp đỡ từ giáo viên và bạn bè.
Lưu ý khi giải bài tập Toán 12
Khi giải bài tập Toán 12, đặc biệt là các bài toán về đạo hàm và ứng dụng đạo hàm, bạn cần:
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
- Nắm vững các kiến thức cơ bản và công thức liên quan.
- Thực hiện các phép tính một cách cẩn thận và chính xác.
- Kiểm tra lại kết quả để đảm bảo tính đúng đắn.
Chúc bạn học tốt và đạt kết quả cao trong môn Toán!
Hãy truy cập tusach.vn để xem thêm nhiều bài giải Toán 12 khác và các tài liệu học tập hữu ích.