Giải bài 1.41 trang 31 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 1.41 trang 31 SBT Toán 12 - Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết bài 1.41 trang 31 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác và đầy đủ nhất, đồng thời giải thích rõ ràng từng bước để bạn có thể hiểu sâu sắc về bài toán.
Bác Hưng có một hàng rào thép dài (240) m và muốn rào cánh đồng thành một thửa ruộng hình chữ nhật giáp một con sông thẳng. Bác không cần rào phía cạnh con sông. Hỏi thửa ruộng có thể tích lớn nhất là bao nhiêu?
Đề bài
Bác Hưng có một hàng rào thép dài \(240\) m và muốn rào cánh đồng thành một thửa ruộng hình chữ nhật giáp một con sông thẳng. Bác không cần rào phía cạnh con sông. Hỏi thửa ruộng có diện tích lớn nhất là bao nhiêu?
Phương pháp giải - Xem chi tiết
+ Đặt độ dài các cạnh của thửa ruộng là các biến \(x,{\rm{ y}}\).
+ Biểu diễn y theo x, từ đó thu được công thức diện tích của thửa ruộng là \(S\left( x \right)\).
+ Tìm giá trị lớn nhất của \(S\left( x \right)\).
Lời giải chi tiết
Gọi độ dài hai cạnh của thửa ruộng hình chữ nhật lần lượt là \(x,{\rm{ y}}\) (m), \(\left( {x,{\rm{ y > }}0} \right)\).
Giả sử cạnh \(y\) giáp với con sông.
Do hàng rào thép dài \(240\) m nên ta có \(2x + y = 240\). Suy ra \(x \le 120\).
Diện tích của thửa ruộng là \(S = xy = x\left( {240 - 2x} \right) = 240x - 2{x^2}\)
Ta có \(S' = 240 - 4x\) khi đó \(S' = 0 \Leftrightarrow 240 - 4x = 0 \Leftrightarrow x = 60\) suy ra \(y = 240 - 2 \cdot 60 = 120\).
Lập bảng biến thiên
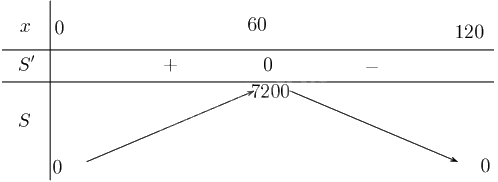
Từ bảng biến thiên suy ra giá trị lớn nhất của hàm số là \(S\left( {60} \right) = 60 \cdot 120 = 7200\).
Vậy thửa ruộng có diện tích lớn nhất là \(7200\) m2 (khi cạnh giáp sông và cạnh đối diện nó có độ dài \(120\) m, độ dài hai cạnh còn lại là \(60\)m.
Giải bài 1.41 trang 31 SBT Toán 12 - Kết nối tri thức: Phân tích và Lời giải Chi Tiết
Bài 1.41 trang 31 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường liên quan đến việc tìm đạo hàm của hàm số, xét tính đơn điệu của hàm số, và tìm cực trị của hàm số.
Nội dung bài tập 1.41 trang 31 SBT Toán 12 - Kết nối tri thức
Thông thường, bài 1.41 sẽ yêu cầu học sinh thực hiện các công việc sau:
- Tính đạo hàm của hàm số đã cho.
- Xác định các điểm mà tại đó đạo hàm bằng 0 hoặc không xác định.
- Khảo sát dấu của đạo hàm trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến của hàm số.
- Tìm các điểm cực trị của hàm số (cực đại, cực tiểu).
Lời giải chi tiết bài 1.41 trang 31 SBT Toán 12 - Kết nối tri thức
Để giải bài 1.41 trang 31 SBT Toán 12 Kết nối tri thức, chúng ta cần thực hiện các bước sau:
- Bước 1: Tính đạo hàm f'(x) của hàm số f(x). Sử dụng các quy tắc tính đạo hàm đã học (quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp, v.v.).
- Bước 2: Tìm các điểm tới hạn. Giải phương trình f'(x) = 0 để tìm các giá trị x mà tại đó đạo hàm bằng 0. Ngoài ra, cần xác định các điểm mà đạo hàm không xác định.
- Bước 3: Lập bảng biến thiên. Chọn các điểm tới hạn và các điểm mà đạo hàm không xác định để chia khoảng xác định của hàm số. Xác định dấu của f'(x) trên mỗi khoảng để xác định khoảng đồng biến, nghịch biến.
- Bước 4: Xác định cực trị. Sử dụng bảng biến thiên để xác định các điểm cực đại, cực tiểu của hàm số.
Ví dụ minh họa (Giả định bài tập cụ thể)
Giả sử bài tập 1.41 yêu cầu giải hàm số f(x) = x3 - 3x2 + 2.
Lời giải:
- Tính đạo hàm: f'(x) = 3x2 - 6x
- Tìm điểm tới hạn: 3x2 - 6x = 0 => 3x(x - 2) = 0 => x = 0 hoặc x = 2
- Lập bảng biến thiên:
x -∞ 0 2 +∞ f'(x) + - + f(x) Đồng biến Nghịch biến Đồng biến - Xác định cực trị:
- Tại x = 0, f'(x) đổi dấu từ dương sang âm, nên x = 0 là điểm cực đại. f(0) = 2. Vậy cực đại là (0, 2).
- Tại x = 2, f'(x) đổi dấu từ âm sang dương, nên x = 2 là điểm cực tiểu. f(2) = -2. Vậy cực tiểu là (2, -2).
Lưu ý khi giải bài tập 1.41 trang 31 SBT Toán 12 - Kết nối tri thức
- Nắm vững các quy tắc tính đạo hàm.
- Cẩn thận khi giải phương trình f'(x) = 0.
- Lập bảng biến thiên một cách chính xác.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Hy vọng với lời giải chi tiết này, bạn đã hiểu rõ cách giải bài 1.41 trang 31 sách bài tập Toán 12 Kết nối tri thức. Chúc bạn học tốt!