Giải bài 2.30 trang 54 sách bài tập toán 12 - Kết nối tri thức
Tổng quan nội dung
Giải bài 2.30 trang 54 SBT Toán 12 - Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết bài 2.30 trang 54 sách bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ cung cấp cho bạn đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những nội dung chất lượng, giúp bạn học Toán 12 hiệu quả hơn.
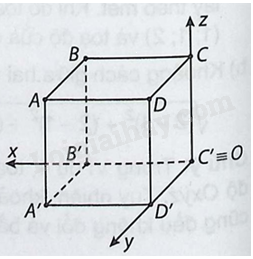
Cho hình lập phương (ABCD.A'B'C'D') có độ dài mỗi cạnh bằng 1. Xét hệ tọa độ (Oxyz) gắn với hình lập phương như hình vẽ bên. a) Tìm tọa độ các đỉnh của hình lập phương. b) Tìm tọa độ trọng tâm (G) của tam giác (B'CD'). c) Chứng minh rằng ba điểm (O,G,A) thẳng hàng.
Đề bài
Cho hình lập phương \(ABCD.A'B'C'D'\) có độ dài mỗi cạnh bằng 1. Xét hệ tọa độ \(Oxyz\) gắn với hình lập phương như hình vẽ bên.
a) Tìm tọa độ các đỉnh của hình lập phương.
b) Tìm tọa độ trọng tâm \(G\) của tam giác \(B'CD'\).
c) Chứng minh rằng ba điểm \(O,G,A\) thẳng hàng.
Phương pháp giải - Xem chi tiết
Ý a: Tìm tọa độ các đỉnh thuộc tia \(Ox,Oy,Oz\) trước, sau đó sử dụng các đẳng thức vectơ bằng nhau để tìm các điểm còn lại. Chú ý sử dụng giả thiết cạnh hình lập phương bằng 1.
Ý b: Dùng công thức tìm tọa độ trọng tâm.
Ý c: Chứng minh \(\overrightarrow {OA} \) và \(\overrightarrow {OG} \) cùng phương bằng đẳng thức \(\overrightarrow {OA} = k\overrightarrow {OG} \).
Lời giải chi tiết
a) Ta có gốc tọa độ là \(C'\) nên \(C'\left( {0;0;0} \right)\); \(B'\) thuộc tia \(Ox\) và \(OB' = 1\) nên \(B'\left( {1;0;0} \right)\); \(D'\) thuộc tia \(Oy\) và \(OD' = 1\) nên \(D'\left( {0;1;0} \right)\); \(C\) thuộc tia \(Oz\) và \(OC = 1\) nên \(C\left( {0;0;1} \right)\).
Ta có \(\overrightarrow {C'C} = \overrightarrow {D'D} \Leftrightarrow \left\{ \begin{array}{l}0 = {x_D}\\0 = {y_D} - 1\\1 = {z_D}\end{array} \right. \Leftrightarrow D\left( {0;1;1} \right)\); \(\overrightarrow {B'B} = \overrightarrow {C'C} \Leftrightarrow \left\{ \begin{array}{l}{x_B} - 1 = 0\\{y_B} = 0\\{z_B} = 1\end{array} \right. \Leftrightarrow B\left( {1;0;1} \right)\);
\(\overrightarrow {B'A'} = \overrightarrow {C'D'} \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} - 1 = 0\\{y_{A'}} = 1\\{z_{A'}} = 0\end{array} \right. \Leftrightarrow A'\left( {1;1;0} \right)\); \(\overrightarrow {A'A} = \overrightarrow {C'C} \Leftrightarrow \left\{ \begin{array}{l}{x_A} - 1 = 0\\{y_A} - 1 = 0\\{z_A} = 1\end{array} \right. \Leftrightarrow A\left( {1;1;1} \right)\).
Vậy \(A\left( {1;1;1} \right)\), \(B\left( {1;0;1} \right)\), \(C\left( {0;0;1} \right)\), \(D\left( {0;1;1} \right)\), \(A'\left( {1;1;0} \right)\), \(B'\left( {1;0;0} \right)\), \(C'\left( {0;0;0} \right)\)
và \(D'\left( {0;1;0} \right)\).
b) Ta có \(B'\left( {1;0;0} \right)\), \(C\left( {0;0;1} \right)\) và \(D'\left( {0;1;0} \right)\) suy ra \(G\left( {\frac{1}{3};\frac{1}{3};\frac{1}{3}} \right)\).
c) Ta có \(\overrightarrow {OG} = \left( {\frac{1}{3};\frac{1}{3};\frac{1}{3}} \right)\); \(\overrightarrow {OA} = \left( {1;1;1} \right)\). Suy ra \(\overrightarrow {OA} = 3\overrightarrow {OG} \). Vậy ba điểm \(O,G,A\) thẳng hàng.
Giải bài 2.30 trang 54 SBT Toán 12 - Kết nối tri thức: Tổng quan
Bài 2.30 trang 54 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tiếp tuyến của đồ thị hàm số, cực trị của hàm số, hoặc các bài toán ứng dụng thực tế.
Nội dung bài 2.30 trang 54 SBT Toán 12 - Kết nối tri thức
Để giải quyết bài 2.30 trang 54 SBT Toán 12 Kết nối tri thức, bạn cần nắm vững các kiến thức sau:
- Đạo hàm: Định nghĩa, ý nghĩa hình học của đạo hàm, các quy tắc tính đạo hàm.
- Tiếp tuyến của đồ thị hàm số: Phương trình tiếp tuyến tại một điểm, điều kiện để đường thẳng là tiếp tuyến của đồ thị hàm số.
- Cực trị của hàm số: Điều kiện cần và đủ để hàm số đạt cực trị, cách tìm cực trị của hàm số.
Lời giải chi tiết bài 2.30 trang 54 SBT Toán 12 - Kết nối tri thức
(Ở đây sẽ là lời giải chi tiết của bài 2.30. Vì không có nội dung cụ thể của bài tập, nên phần này sẽ được mô tả chung. Cần thay thế bằng lời giải chính xác khi có đề bài.)
Để giải bài tập này, ta thực hiện các bước sau:
- Bước 1: Xác định hàm số và các thông tin đã cho trong đề bài.
- Bước 2: Tính đạo hàm của hàm số.
- Bước 3: Sử dụng đạo hàm để tìm các điểm cực trị hoặc phương trình tiếp tuyến (tùy theo yêu cầu của bài).
- Bước 4: Kiểm tra lại kết quả và trình bày lời giải một cách rõ ràng, logic.
Ví dụ minh họa
(Ở đây sẽ là một ví dụ minh họa tương tự bài 2.30 để giúp học sinh hiểu rõ hơn về phương pháp giải. Cần thay thế bằng ví dụ phù hợp khi có đề bài.)
Lưu ý khi giải bài tập
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài tập.
- Sử dụng các công thức và quy tắc đạo hàm một cách chính xác.
- Kiểm tra lại kết quả để đảm bảo tính đúng đắn.
- Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải bài tập.
Các bài tập tương tự
Để củng cố kiến thức, bạn có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 12 Kết nối tri thức hoặc trên các trang web học Toán trực tuyến.
Tusach.vn - Nguồn tài liệu học Toán 12 uy tín
Tusach.vn là một trang web cung cấp đầy đủ các tài liệu học Toán 12, bao gồm sách giáo khoa, sách bài tập, đề thi, và lời giải chi tiết. Chúng tôi cam kết mang đến cho bạn những tài liệu chất lượng, giúp bạn học Toán 12 hiệu quả và đạt kết quả cao.
| Chương | Bài | Liên kết |
|---|---|---|
| 1 | 1.1 | Giải bài 1.1 trang 8 |
| 2 | 2.2 | Giải bài 2.2 trang 20 |