Lý Thuyết Vecto Toán 12 Chân Trời Sáng Tạo

Lý thuyết Vecto và các phép toán trong không gian Toán 12 Chân trời sáng tạo

Lý thuyết Vecto và các phép toán trong không gian - Nền tảng Toán 12

Lý thuyết Vecto là một trong những chủ đề quan trọng của chương trình Toán 12 Chân trời sáng tạo. Nắm vững kiến thức về vectơ sẽ giúp học sinh giải quyết các bài toán về hình học không gian một cách hiệu quả.

Bài viết này sẽ cung cấp đầy đủ lý thuyết, ví dụ minh họa và bài tập áp dụng để bạn có thể hiểu sâu sắc về vectơ và các phép toán liên quan.

Bài 1. Vecto và các phép toán trong không gian 1. Vecto trong không gian

1. Vecto trong không gian

Vecto trong không gian là một đoạn thẳng có hướng
Các khái niệm có liên quan đến vecto trong không gian như: giá của vecto, độ dài của vecto, vecto cùng phương, vecto cùng hướng, vecto-không, hai vecto bằng nhau, hai vecto đối nhau, … được phát biểu tương tự như trong mặt phẳng

2. Tổng và hiệu của hai vecto

a) Tổng của hai vecto

Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Lấy một điểm A bất kì và các điểm B,C sao cho \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Khi đó, vecto \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu là \(\overrightarrow a + \overrightarrow b \)

Phép lấy tổng của hai vecto được gọi là phép cộng vecto

Với 3 điểm A, B, C trong không gian, ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (Quy tắc 3 điểm)
Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (Quy tắc hình bình hành)
Nếu ABCD.A’B’C’D’ là hình hộp thì \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)(Quy tắc hình hộp)

b) Hiệu của hai vecto

Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Hiệu của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là tổng của hai vecto \(\mathop a\limits^ \to \) và vecto đối của \(\mathop b\limits^ \to \), kí hiệu là \(\mathop a\limits^ \to - \mathop b\limits^ \to \)

Phép lấy hiệu của hai vecto được gọi là phép trừ vecto

Với ba điểm O, A, B trong không gian, ta có: \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \) (Quy tắc hiệu)

3. Tích của một số với một vecto

Trong không gian, tích của một số thực \(k \ne 0\) với một vecto \(\overrightarrow a \ne \overrightarrow 0 \) là một vecto, kí hiệu là \(k\overrightarrow a \), được xác định như sau:

- Cùng hướng với vecto \(\mathop a\limits^ \to \) nếu k > 0; ngược hướng với vecto \(\mathop a\limits^ \to \) nếu k < 0

- Có độ dài bằng \(\left| k \right|.\left| {\overrightarrow a } \right|\)

Phép lấy tích của một số với một vecto được gọi là phép nhân một số với một vecto

4. Tích vô hướng của hai vecto

a) Góc giữa hai vecto trong không gian

Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}({0^ \circ } \le \widehat {AOB} \le {180^ \circ })\) được gọi là góc giữa hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu \(\left( {\overrightarrow a ,\overrightarrow b } \right)\)

b) Tích vô hướng của hai vecto

Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Tích vô hướng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)

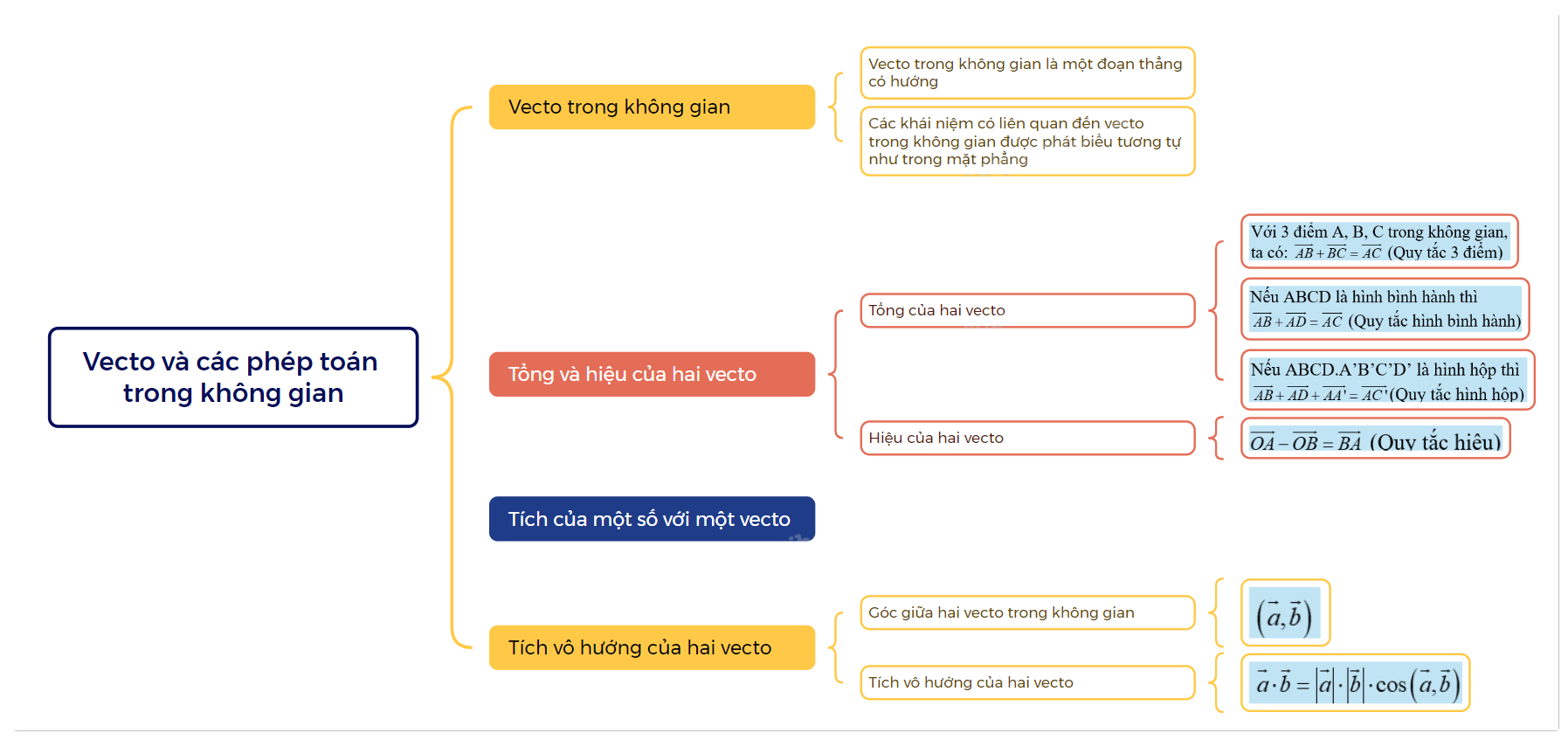
Lý Thuyết Vecto và Các Phép Toán Trong Không Gian Toán 12 Chân Trời Sáng Tạo

Chào mừng các em học sinh đến với bài viết tổng hợp lý thuyết và phương pháp giải các bài toán liên quan đến vectơ trong không gian, thuộc chương trình Toán 12 Chân Trời Sáng Tạo. Đây là một phần kiến thức quan trọng, nền tảng cho việc giải quyết các bài toán hình học không gian phức tạp hơn.

1. Khái Niệm Cơ Bản Về Vectơ

Vectơ là một đoạn thẳng có hướng. Nó được xác định bởi điểm gốc và điểm cuối. Vectơ được ký hiệu là AB, trong đó A là điểm gốc và B là điểm cuối.

Độ dài của vectơ: Khoảng cách giữa điểm gốc và điểm cuối.
Hướng của vectơ: Hướng của đoạn thẳng.
Vectơ chỉ phương: Vectơ có hướng trùng với hướng của đường thẳng.

2. Các Phép Toán Vectơ Cơ Bản

Trong không gian, chúng ta thực hiện các phép toán vectơ sau:

Phép cộng vectơ:AB + BC = AC (Quy tắc tam giác hoặc quy tắc hình bình hành).
Phép trừ vectơ:AB - BC = AC
Phép nhân vectơ với một số thực: k.AB (Vectơ mới có độ dài gấp k lần độ dài của AB, cùng hướng nếu k > 0 và ngược hướng nếu k < 0).

3. Tích Vô Hướng của Hai Vectơ

Tích vô hướng của hai vectơ a và b, ký hiệu là a.b, được tính bằng công thức:

a.b = |a||b|cos(θ), trong đó θ là góc giữa hai vectơ.

Nếu a.b = 0 thì hai vectơ vuông góc.
Ứng dụng: Tính góc giữa hai vectơ, kiểm tra tính vuông góc.

4. Tích Có Hướng của Hai Vectơ

Tích có hướng của hai vectơ a và b, ký hiệu là a x b, là một vectơ có:

Hướng: Vuông góc với cả hai vectơ a và b, tuân theo quy tắc bàn tay phải.
Độ dài:|a x b| = |a||b|sin(θ)

Ứng dụng: Tính diện tích hình bình hành, kiểm tra tính đồng phẳng của ba vectơ.

5. Ứng Dụng của Vectơ trong Hình Học Không Gian

Vectơ được sử dụng để:

Biểu diễn các điểm, đường thẳng, mặt phẳng trong không gian.
Chứng minh các tính chất hình học.
Giải các bài toán về khoảng cách, góc, vị trí tương đối của các đối tượng hình học.

6. Bài Tập Vận Dụng

Dưới đây là một số bài tập vận dụng để các em luyện tập:

Cho hai vectơ a = (1; 2; 3) và b = (-2; 1; 0). Tính a.b và a x b.
Cho A(1; 2; 3), B(2; 4; 5), C(3; 6; 7). Chứng minh A, B, C thẳng hàng.
Tính diện tích hình bình hành có hai cạnh là a = (1; 0; 0) và b = (0; 1; 0).

Hy vọng bài viết này đã cung cấp cho các em những kiến thức cơ bản và hữu ích về lý thuyết vectơ và các phép toán trong không gian. Chúc các em học tập tốt!