Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Bài tập trong mục này tập trung vào các kiến thức về...
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn
TH3
Trả lời câu hỏi Thực hành 3 trang 18 SGK Toán 12 Chân trời sáng tạo
Tam giác vuông có cạnh huyền bằng 5 cm có thể có diện tích lớn nhất bằng bao nhiêu?
Phương pháp giải:
Tìm hệ thức liên hệ giữa các cạnh, từ đó suy ra hàm số của diện tích tam giác vuông. Sau đó tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất của hàm số
Lời giải chi tiết:
Đặt một cạnh góc vuông là x (x > 0) thì cạnh còn lại là \(\sqrt {25 - {x^2}} \)
Diện tích tam giác vuông là: \(f(x) = \frac{{1}}{2} x\sqrt {25 - {x^2}} \)
Tập xác định: \(D = (0; 5 )\)
\(f'(x) = \frac{{1}}{2}\sqrt {25 - {x^2}} - \frac{{1}}{2}. \frac{{{x^2}}}{{\sqrt {25 - {x^2}} }}\)
Tập xác định mới: \({D_1} = (0; 5 )\)
\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\sqrt {2} }}{2}\\x = - \frac{{5\sqrt {2} }}{2}(loại)\end{array} \right.\)
Bảng biến thiên:
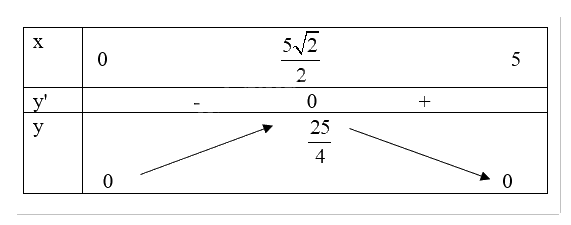
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_D f(x) = f(\frac{{5\sqrt {2} }}{2}) = \frac{25}{4}\).
Vậy diện tích lớn nhất của tam giác là \(\frac{25}{4}\).
TH2
Trả lời câu hỏi Thực hành 2 trang 18 SGK Toán 12 Chân trời sáng tạo
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(g(x) = x + \frac{4}{{{x^2}}}\) trên đoạn [1;4]
Phương pháp giải:
Tìm đạo hàm g’(x), lập bảng biến thiên và xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Lời giải chi tiết:
Xét \(g(x) = x + \frac{4}{{{x^2}}}\) trên đoạn [1;4]
\(g'(x) = 1 - \frac{8}{{{x^3}}} = 0 \Leftrightarrow x = 2\)
Bảng biến thiên:
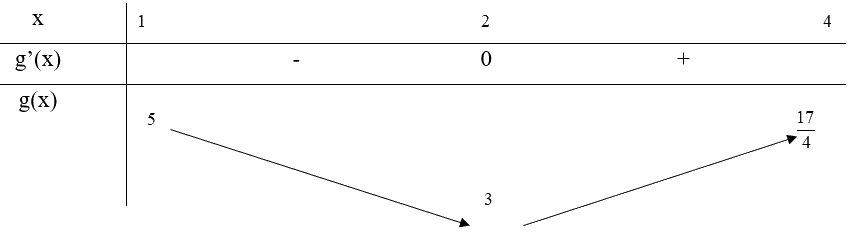
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[1;4]} g(x) = g(2) = 3\) và \(\mathop {\max }\limits_{[1;4]} g(x) = g(1) = 5\)
KP2
Trả lời câu hỏi Khám phá 2 trang 16 SGK Toán 12 Chân trời sáng tạo
Hình 3 cho ta đồ thị của ba hàm số
\(f(x) = \frac{1}{2}{x^2}\); \(g(x) = \left\{ \begin{array}{l}\frac{1}{2}{x^2}\;\;\;\;\;\;\;\;\;\;\;neu\;x \le 2\;\\ - 4x + 10\;\;\;\;neu\;x \ge 2\end{array} \right.\) và \(h(x) = 3 - \frac{1}{2}{x^2}\) trên đoạn [-1;3]
a) Hàm số nào đạt giá trị lớn nhất tại một điểm cực đại của nó?
b) Các hàm số còn lại đạt giá trị lớn nhất tại điểm nào?
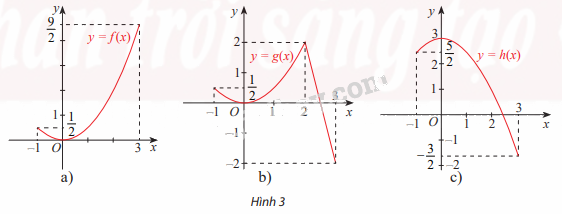
Phương pháp giải:
Quan sát đồ thị và chỉ ra điểm cực đại và giá trị lớn nhất của 3 hàm số.
Lời giải chi tiết:
a) \(h(x)\)đạt giá trị cực đại tại x = 0 và \(\mathop {\max h(x)}\limits_{[ - 1;3]} = h(0) = 3\)
b) \(\mathop {\max f(x)}\limits_{[ - 1;3]} = f(3) = \frac{9}{2}\) và \(\mathop {\max g(x)}\limits_{[ - 1;3]} = g(2) = 2\)
- KP2
- TH2
- TH3
Trả lời câu hỏi Khám phá 2 trang 16 SGK Toán 12 Chân trời sáng tạo
Hình 3 cho ta đồ thị của ba hàm số
\(f(x) = \frac{1}{2}{x^2}\); \(g(x) = \left\{ \begin{array}{l}\frac{1}{2}{x^2}\;\;\;\;\;\;\;\;\;\;\;neu\;x \le 2\;\\ - 4x + 10\;\;\;\;neu\;x \ge 2\end{array} \right.\) và \(h(x) = 3 - \frac{1}{2}{x^2}\) trên đoạn [-1;3]
a) Hàm số nào đạt giá trị lớn nhất tại một điểm cực đại của nó?
b) Các hàm số còn lại đạt giá trị lớn nhất tại điểm nào?
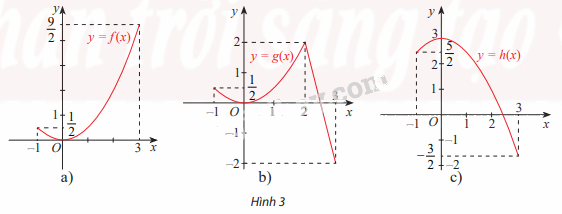
Phương pháp giải:
Quan sát đồ thị và chỉ ra điểm cực đại và giá trị lớn nhất của 3 hàm số.
Lời giải chi tiết:
a) \(h(x)\)đạt giá trị cực đại tại x = 0 và \(\mathop {\max h(x)}\limits_{[ - 1;3]} = h(0) = 3\)
b) \(\mathop {\max f(x)}\limits_{[ - 1;3]} = f(3) = \frac{9}{2}\) và \(\mathop {\max g(x)}\limits_{[ - 1;3]} = g(2) = 2\)
Trả lời câu hỏi Thực hành 2 trang 18 SGK Toán 12 Chân trời sáng tạo
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(g(x) = x + \frac{4}{{{x^2}}}\) trên đoạn [1;4]
Phương pháp giải:
Tìm đạo hàm g’(x), lập bảng biến thiên và xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Lời giải chi tiết:
Xét \(g(x) = x + \frac{4}{{{x^2}}}\) trên đoạn [1;4]
\(g'(x) = 1 - \frac{8}{{{x^3}}} = 0 \Leftrightarrow x = 2\)
Bảng biến thiên:
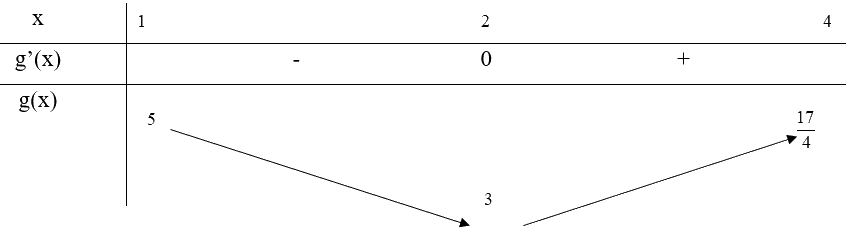
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[1;4]} g(x) = g(2) = 3\) và \(\mathop {\max }\limits_{[1;4]} g(x) = g(1) = 5\)
Trả lời câu hỏi Thực hành 3 trang 18 SGK Toán 12 Chân trời sáng tạo
Tam giác vuông có cạnh huyền bằng 5 cm có thể có diện tích lớn nhất bằng bao nhiêu?
Phương pháp giải:
Tìm hệ thức liên hệ giữa các cạnh, từ đó suy ra hàm số của diện tích tam giác vuông. Sau đó tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất của hàm số
Lời giải chi tiết:
Đặt một cạnh góc vuông là x (x > 0) thì cạnh còn lại là \(\sqrt {25 - {x^2}} \)
Diện tích tam giác vuông là: \(f(x) = \frac{{1}}{2} x\sqrt {25 - {x^2}} \)
Tập xác định: \(D = (0; 5 )\)
\(f'(x) = \frac{{1}}{2}\sqrt {25 - {x^2}} - \frac{{1}}{2}. \frac{{{x^2}}}{{\sqrt {25 - {x^2}} }}\)
Tập xác định mới: \({D_1} = (0; 5 )\)
\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\sqrt {2} }}{2}\\x = - \frac{{5\sqrt {2} }}{2}(loại)\end{array} \right.\)
Bảng biến thiên:
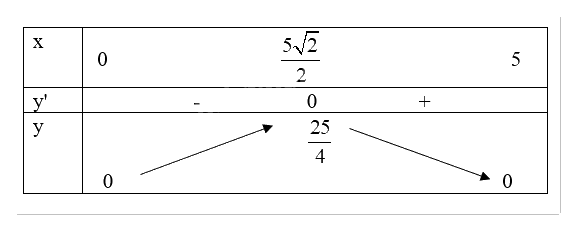
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_D f(x) = f(\frac{{5\sqrt {2} }}{2}) = \frac{25}{4}\).
Vậy diện tích lớn nhất của tam giác là \(\frac{25}{4}\).
Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 2 của SGK Toán 12 tập 1 chương trình Chân trời sáng tạo là một phần quan trọng, đặt nền móng cho việc hiểu và vận dụng các kiến thức về đạo hàm trong các bài học tiếp theo. Nội dung chính của mục này xoay quanh việc tìm hiểu về giới hạn của hàm số, ý nghĩa hình học của giới hạn và các tính chất cơ bản của giới hạn. Việc nắm vững kiến thức này không chỉ giúp các em giải quyết các bài tập trong SGK mà còn là bước đệm quan trọng cho việc học tập các môn khoa học khác.
Nội dung chính của Mục 2
- Khái niệm giới hạn của hàm số: Hiểu rõ định nghĩa giới hạn của hàm số tại một điểm và trên một khoảng.
- Ý nghĩa hình học của giới hạn: Liên hệ giữa giới hạn của hàm số và đồ thị hàm số.
- Các tính chất của giới hạn: Vận dụng các tính chất của giới hạn để tính toán giới hạn của các hàm số phức tạp.
- Các dạng giới hạn cơ bản: Nắm vững các dạng giới hạn thường gặp và cách giải quyết chúng.
Giải chi tiết các bài tập trang 16, 17, 18
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 Chân trời sáng tạo:
Bài 1: (Trang 16)
Đề bài: ... (Nội dung đề bài)
Lời giải: ... (Lời giải chi tiết, bao gồm các bước giải và giải thích rõ ràng)
Bài 2: (Trang 17)
Đề bài: ... (Nội dung đề bài)
Lời giải: ... (Lời giải chi tiết, bao gồm các bước giải và giải thích rõ ràng)
Bài 3: (Trang 18)
Đề bài: ... (Nội dung đề bài)
Lời giải: ... (Lời giải chi tiết, bao gồm các bước giải và giải thích rõ ràng)
Mẹo giải bài tập hiệu quả
- Nắm vững định nghĩa: Hiểu rõ định nghĩa của giới hạn và các khái niệm liên quan.
- Vận dụng tính chất: Sử dụng các tính chất của giới hạn để đơn giản hóa bài toán.
- Phân tích kỹ đề bài: Xác định rõ yêu cầu của đề bài và lựa chọn phương pháp giải phù hợp.
- Kiểm tra lại kết quả: Đảm bảo kết quả cuối cùng là chính xác và hợp lý.
Tài liệu tham khảo thêm
Để hiểu sâu hơn về nội dung Mục 2, các em có thể tham khảo thêm các tài liệu sau:
- Sách giáo khoa Toán 12 tập 1 Chân trời sáng tạo
- Sách bài tập Toán 12 tập 1 Chân trời sáng tạo
- Các trang web học toán trực tuyến uy tín
Tusach.vn hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc giải quyết các bài tập về giới hạn của hàm số. Chúc các em học tập tốt!