Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài tập 14 trang 38 SGK Toán 12 tập 1 - Chân trời sáng tạo
SGK Toán 12 - Chân trời sáng tạo
Giải Toán 12 tập 1 - Chân trời sáng tạo
Chương 1. Ứng dụng đạo hàm để khảo sát hàm số
Bài tập cuối chương 1

Giải bài tập 14 trang 38 SGK Toán 12 tập 1 - Chân trời sáng tạo

Giải Bài Tập 14 Trang 38 Toán 12 Tập 1 - Chân Trời Sáng Tạo

Chào mừng bạn đến với lời giải chi tiết bài tập 14 trang 38 SGK Toán 12 tập 1 Chân trời sáng tạo trên tusach.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp bạn hiểu sâu sắc kiến thức và tự tin làm bài tập.

Chúng tôi luôn cố gắng mang đến những nội dung chất lượng, cập nhật nhanh chóng và dễ dàng tiếp cận.

Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b

Đề bài

Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b

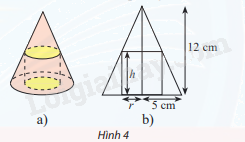
Giải bài tập 14 trang 38 SGK Toán 12 tập 1 - Chân trời sáng tạo 1

a) Chứng minh rằng công thức tính bán kính r của đáy hình trụ theo chiều cao h của nó là: \(r = \frac{{5(12 - h)}}{{12}}\)

b) Chứng minh biểu thức sau biểu thị thể tích khối trụ theo h: \(V(h) = \frac{{25\pi h{{(12 - h)}^2}}}{{144}}\)

c) Tìm h để khối trụ có thể tích lớn nhất.

Phương pháp giải - Xem chi tiếtGiải bài tập 14 trang 38 SGK Toán 12 tập 1 - Chân trời sáng tạo 2

a) Từ hình vẽ, tìm mối liên hệ giữa r và h thông qua các công thức tính diện tích, thể tích,….

b) Thể tích khối trụ là \(V = \pi {r^2}h\)

c) Lập bảng biến thiên và quan sát

Lời giải chi tiết

a) Xét nửa tam giác lớn Hình 4b. Diện tích hình chữ nhật bằng diện tích tam giác lớn trừ diện tích hai tam giác nhỏ. Ta có: \(rh = \frac{1}{2}.12.5 - \frac{1}{2}.h(5 - r) - \frac{1}{2}(12 - h).r = \frac{{60 - 5h + rh - 12r + rh}}{2}\)

\( \Leftrightarrow 2rh = 60 - 5h + 2rh - 12r \Leftrightarrow 12r = 60 - 5h \Leftrightarrow r = \frac{{5(12 - h)}}{{12}}\)

b) Thể tích khối trụ là: \(V(h) = \pi {r^2}h = \pi .\frac{{{5^2}{{(12 - h)}^2}}}{{{{12}^2}}}h = \frac{{25\pi h{{(12 - h)}^2}}}{{144}}\)

c) Thể tích khối trụ lớn nhất khi V(h) đạt giá trị lớn nhất. Ta tìm max của hàm V(h) bằng cách tìm đạo hàm V'(h) và lập bảng biến thiên.

\(V'(h) = \frac{{75\pi {h^2} - 1200\pi h + 3600\pi }}{{144}} = 0 \Leftrightarrow \left[ \begin{array}{l}h = 4\\h = 12\end{array} \right.\)

Bảng biến thiên:

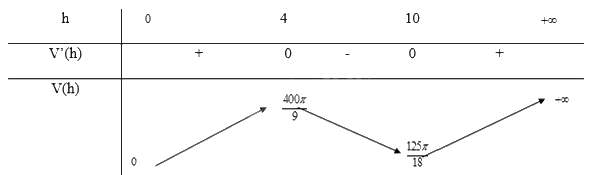
Giải bài tập 14 trang 38 SGK Toán 12 tập 1 - Chân trời sáng tạo 3

Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{(0; + \infty )} V(h) = V(4) = \frac{{400\pi }}{9}\)

Vậy để khối trụ có thể tích lớn nhất thì h = 4cm

Giải Bài Tập 14 Trang 38 Toán 12 Tập 1 - Chân Trời Sáng Tạo: Hướng Dẫn Chi Tiết

Bài tập 14 trang 38 SGK Toán 12 tập 1 Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học nâng cao hơn. Việc nắm vững phương pháp giải các bài tập về giới hạn sẽ giúp học sinh tự tin hơn trong các kỳ thi.

Nội Dung Bài Tập 14 Trang 38

Bài tập 14 yêu cầu tính giới hạn của hàm số khi x tiến tới một giá trị nhất định. Các dạng bài tập thường gặp bao gồm:

  • Tính giới hạn bằng cách sử dụng định nghĩa giới hạn.
  • Tính giới hạn bằng cách sử dụng các tính chất của giới hạn.
  • Tính giới hạn của hàm số hữu tỉ.
  • Tính giới hạn của hàm số vô tỉ.

Lời Giải Chi Tiết Bài Tập 14a

Đề bài: Tính limx→2 (x2 - 4) / (x - 2)

Lời giải:

  1. Ta có thể phân tích tử số thành nhân tử: x2 - 4 = (x - 2)(x + 2)
  2. Khi đó, biểu thức trở thành: limx→2 (x - 2)(x + 2) / (x - 2)
  3. Rút gọn (x - 2) ở tử và mẫu, ta được: limx→2 (x + 2)
  4. Thay x = 2 vào biểu thức, ta được: 2 + 2 = 4
  5. Vậy, limx→2 (x2 - 4) / (x - 2) = 4

Lời Giải Chi Tiết Bài Tập 14b

Đề bài: Tính limx→3 (x3 - 27) / (x - 3)

Lời giải:

  1. Ta có thể phân tích tử số thành nhân tử: x3 - 27 = (x - 3)(x2 + 3x + 9)
  2. Khi đó, biểu thức trở thành: limx→3 (x - 3)(x2 + 3x + 9) / (x - 3)
  3. Rút gọn (x - 3) ở tử và mẫu, ta được: limx→3 (x2 + 3x + 9)
  4. Thay x = 3 vào biểu thức, ta được: 32 + 3*3 + 9 = 9 + 9 + 9 = 27
  5. Vậy, limx→3 (x3 - 27) / (x - 3) = 27

Mẹo Giải Bài Tập Về Giới Hạn

Để giải các bài tập về giới hạn một cách hiệu quả, bạn nên:

  • Nắm vững định nghĩa giới hạn và các tính chất của giới hạn.
  • Thành thạo các phương pháp phân tích đa thức thành nhân tử.
  • Sử dụng máy tính bỏ túi để kiểm tra kết quả.
  • Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.

Tầm Quan Trọng Của Việc Giải Bài Tập

Việc giải bài tập không chỉ giúp bạn hiểu sâu sắc kiến thức mà còn rèn luyện kỹ năng giải quyết vấn đề. Hãy dành thời gian để tự mình giải các bài tập trước khi xem lời giải. Điều này sẽ giúp bạn tự tin hơn trong các kỳ thi và áp dụng kiến thức vào thực tế.

Hy vọng với lời giải chi tiết và hướng dẫn trên, bạn đã hiểu rõ cách giải bài tập 14 trang 38 SGK Toán 12 tập 1 Chân trời sáng tạo. Chúc bạn học tốt!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN