Đề bài
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{{x^2} - 2x + 2}}{{x - 1}}\)
b) \(y = 2x - \frac{1}{{1 - 2x}}\)
Phương pháp giải - Xem chi tiết
Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực và các tiệm cận của đồ thị hàm số (nếu có)
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
Lời giải chi tiết
a) \(y = \frac{{{x^2} - 2x + 2}}{{x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 1\} \)
\(y' = \frac{{{x^2} - 2x}}{{{{(x - 1)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Trên các khoảng (\( - \infty \); 0), (2; \( + \infty \)) thì y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó. Trên khoảng (0; 2) thì y' > 0 nên hàm số đồng biến trên khoảng đó.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 2x + 2}}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} - 2x + 2}}{{x - 1}} = - \infty \)
\(a = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 2x + 2}}{{{x^2} - x}} = 1;b = \mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} - 2x + 2}}{{x - 1}} - x) = - 1\) nên y = x - 1 là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 2x + 2}}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 2x + 2}}{{x - 1}} = - \infty \) nên x = 1 là tiệm cận đứng của đồ thị hàm số
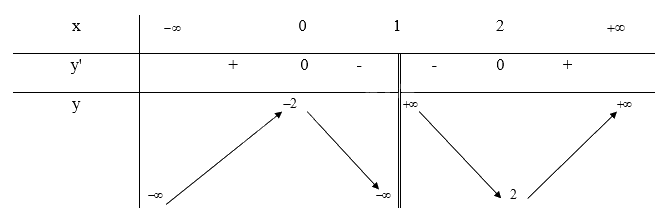
Khi x = 0 thì y = -2 nên (0;-2) là giao điểm của y với trục Oy
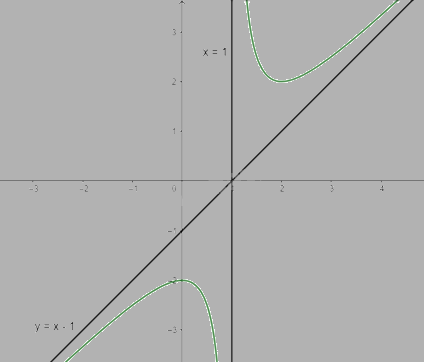
b) \(y = 2x - \frac{1}{{1 - 2x}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ \frac{1}{2}\} \)
\(y' = 2 - \frac{2}{{{{(1 - 2x)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)
Trên các khoảng (\( - \infty \); 0), (1; \( + \infty \)) thì y' > 0 nên hàm số nghịch biến trên mỗi khoảng đó. Trên khoảng (0; \(\frac{1}{2}\)) và (\(\frac{1}{2}\); 1) thì y' < 0 nên hàm số đồng biến trên khoảng đó.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } (2x - \frac{1}{{1 - 2x}}) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } (2x - \frac{1}{{1 - 2x}}) = - \infty \)
\(a = \mathop {\lim }\limits_{x \to + \infty } (2 - \frac{1}{{x - 2{x^2}}}) = 2;b = \mathop {\lim }\limits_{x \to + \infty } (2x - \frac{1}{{1 - 2x}} - 2x) = 0\) nên y = 2x là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} y = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} (2x - \frac{1}{{1 - 2x}}) = + \infty ;\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} y = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} (2x - \frac{1}{{1 - 2x}}) = - \infty \) nên x = \(\frac{1}{2}\) là tiệm cận đứng của đồ thị hàm số
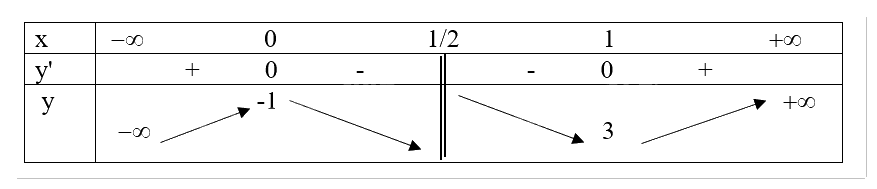
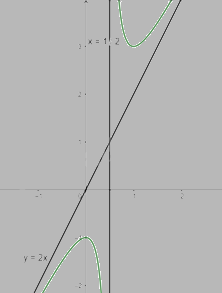
Khi x = 0 thì y = -1 nên (0;-1) là giao điểm của y với trục Oy
