Giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo

Bài tập 9 trang 37 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Chân trời sáng tạo. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

Tìm hai số không âm a và b có tổng bằng 10 sao cho: a) Biểu thức ab đạt giá trị lớn nhất; b) Tổng bình phương của chúng đạt giá trị nhỏ nhất; c) Biểu thức (a{b^2}) đạt giá trị lớn nhất

Đề bài

Tìm hai số không âm a và b có tổng bằng 10 sao cho:

a) Biểu thức ab đạt giá trị lớn nhất;

b) Tổng bình phương của chúng đạt giá trị nhỏ nhất;

c) Biểu thức \(a{b^2}\) đạt giá trị lớn nhất

Phương pháp giải - Xem chi tiết Giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo 1

Tìm biểu thức liên hệ của a theo b hoặc ngược lại. Sau đó lập hàm số theo a hoặc b, lập bảng biến thiên và quan sát

Lời giải chi tiết

Ta có: a, b > 0 và a + b = 10

a) Đặt: \(f(a) = ab = a(10 - a) = - {a^2} + 10a\)

\(f'(a) = - 2a + 10 = 0 \Leftrightarrow a = 5\)

Bảng biến thiên:

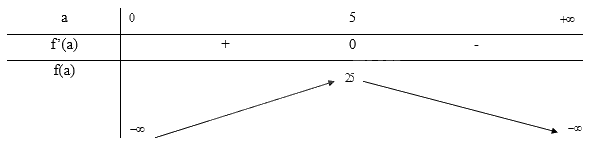
Giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo 2

Từ bảng biến thiên ta thấy, \(\mathop {\max }\limits_{(0; + \infty )} f(a) = f(5) = 25\)

Vậy để biểu thức ab đạt giá trị lớn nhất là 25 thì a = 5 và b = 5

b) Đặt: \(f(a) = {a^2} + {b^2} = {a^2} + {(10 - a)^2} = 2{a^2} - 20a + 100\)

\(f'(a) = 4a - 20 = 0 \Leftrightarrow a = 5\)

Bảng biến thiên:

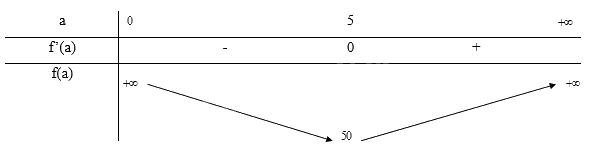
Giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo 3

Từ bảng biến thiên ta thấy, \(\mathop {\min }\limits_{(0; + \infty )} f(a) = f(5) = 50\)

Vậy để biểu thức \({a^2} + {b^2}\) đạt giá trị nhỏ nhất là 50 thì a = 5 và b = 5

c) Đặt: \(f(a) = a{b^2} = a{(10 - a)^2} = {a^3} - 20{a^2} + 100a\)

\(f'(a) = 3{a^2} - 40a + 100 = 0 \Leftrightarrow \left[ \begin{array}{l}a = \frac{{10}}{3}\\a = 10\end{array} \right.\)

Bảng biến thiên:

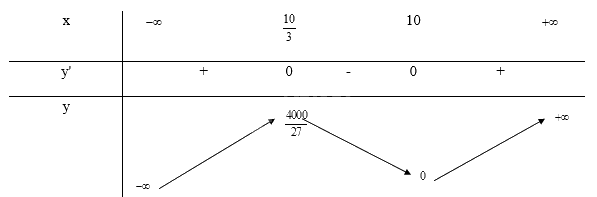
Giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo 4

Từ bảng biến thiên ta thấy, \(\mathop {\max }\limits_{(0; + \infty )} f(a) = f(\frac{{10}}{3}) = \frac{{4000}}{{27}}\)

Vậy để biểu thức \(a{b^2}\) đạt giá trị lớn nhất là \(\frac{{4000}}{{27}}\) thì a = \(\frac{{10}}{3}\) và b = \(\frac{{20}}{3}\)

Giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu

Bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 12, tập trung vào việc rèn luyện kỹ năng tính giới hạn của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các định lý liên quan và các phương pháp tính giới hạn thường gặp.

Nội dung bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo

Bài tập 9 thường có dạng yêu cầu tính giới hạn của một hàm số khi x tiến tới một giá trị cụ thể. Hàm số có thể là hàm đa thức, hàm hữu tỉ, hoặc hàm lượng giác. Việc xác định đúng dạng hàm số và áp dụng phương pháp tính giới hạn phù hợp là chìa khóa để giải quyết bài tập này.

Phương pháp giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo

Có nhiều phương pháp để tính giới hạn của hàm số, tùy thuộc vào dạng hàm số cụ thể. Dưới đây là một số phương pháp thường được sử dụng:

Phương pháp trực tiếp: Thay trực tiếp giá trị của x vào hàm số để tính giới hạn. Phương pháp này chỉ áp dụng được khi hàm số liên tục tại điểm x.
Phương pháp phân tích thành nhân tử: Phân tích tử số và mẫu số thành nhân tử để rút gọn biểu thức và loại bỏ các yếu tố gây ra vô định thức.
Phương pháp nhân liên hợp: Nhân cả tử số và mẫu số với liên hợp của biểu thức chứa căn thức để loại bỏ căn thức và đơn giản hóa biểu thức.
Phương pháp sử dụng định lý giới hạn: Áp dụng các định lý giới hạn đã học để tính giới hạn của hàm số.

Lời giải chi tiết bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo

(Ở đây sẽ là lời giải chi tiết của bài tập 9, bao gồm các bước giải, giải thích rõ ràng và kết quả cuối cùng. Ví dụ:)

Bài tập: Tính lim_x→2 (x² - 4) / (x - 2)

Lời giải:

Phân tích tử số thành nhân tử: x² - 4 = (x - 2)(x + 2)
Rút gọn biểu thức: (x² - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2
Tính giới hạn: lim_x→2 (x + 2) = 2 + 2 = 4

Kết luận:lim_x→2 (x² - 4) / (x - 2) = 4

Lưu ý khi giải bài tập về giới hạn

Luôn kiểm tra xem hàm số có liên tục tại điểm x hay không trước khi áp dụng phương pháp trực tiếp.
Khi phân tích thành nhân tử, hãy tìm các nhân tử chung để rút gọn biểu thức.
Sử dụng phương pháp nhân liên hợp một cách cẩn thận để tránh sai sót.
Nắm vững các định lý giới hạn và áp dụng chúng một cách linh hoạt.

Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín

Tusach.vn là một website cung cấp đầy đủ các tài liệu học tập Toán 12, bao gồm sách giáo khoa, sách bài tập, đề thi và lời giải chi tiết. Chúng tôi cam kết cung cấp cho bạn những thông tin chính xác, hữu ích và dễ hiểu nhất. Hãy truy cập Tusach.vn để học tập và ôn luyện Toán 12 hiệu quả!

Hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo và đạt kết quả tốt trong môn Toán.

Giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo

Giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo

Giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu

Nội dung bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo

Phương pháp giải bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo

Lời giải chi tiết bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo

Lưu ý khi giải bài tập về giới hạn

Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN