Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Tusach.vn xin giới thiệu lời giải chi tiết bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo. Bài tập này thuộc chương trình học Toán 12, tập trung vào các kiến thức về giới hạn của hàm số.

Chúng tôi cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu sắc kiến thức và tự tin làm bài tập.

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: a) (y = {x^3} - 12x + 1) trên đoạn [-1;3] b) (y = - {x^3} + 24{x^2} - 180x + 400) trên đoạn [3;11] c) (y = frac{{2x + 1}}{{x - 2}}) trên đoạn [3;7] d) (y = sin 2x) trên đoạn ([0;frac{{7pi }}{{12}}])

Đề bài

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) \(y = {x^3} - 12x + 1\) trên đoạn [-1;3] b) \(y = - {x^3} + 24{x^2} - 180x + 400\) trên đoạn [3;11]c) \(y = \frac{{2x + 1}}{{x - 2}}\) trên đoạn [3;7] d) \(y = \sin 2x\) trên đoạn \([0;\frac{{7\pi }}{{12}}]\)

Phương pháp giải - Xem chi tiết Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo 1

Tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số

Lời giải chi tiết

a) Xét \(y = {x^3} - 12x + 1\) trên đoạn [-1;3]

\(y' = 3{x^2} - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2(loai)\end{array} \right.\)

Bảng biến thiên:

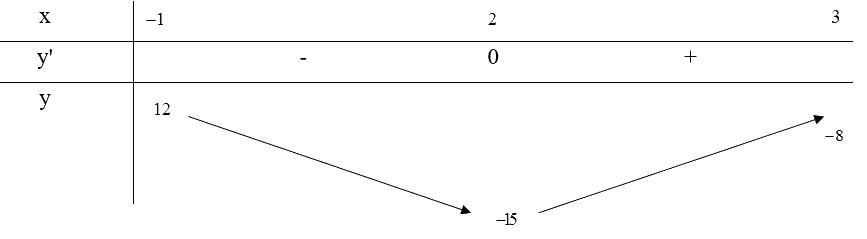
Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo 2

Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[ - 1;3]} y = y( - 1) = 12\) và \(\mathop {\min }\limits_{[ - 1;3]} y = y(2) = - 15\)

b) Xét \(y = - {x^3} + 24{x^2} - 180x + 400\) trên đoạn [3;11]

\(y' = - 3{x^2} + 48x - 180 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 10\\x = 6\end{array} \right.\)

Bảng biến thiên:

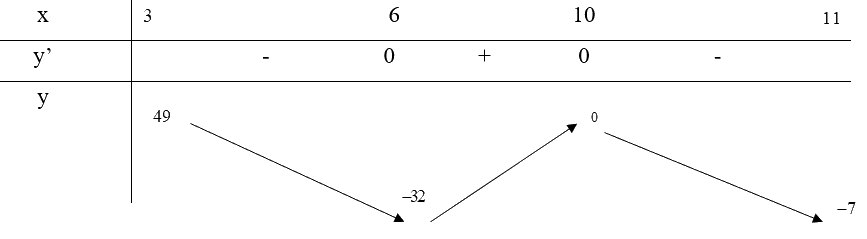
Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo 3

Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[3;11]} y = y(3) = 49\) và \(\mathop {\min }\limits_{[3;11]} y = y(6) = - 32\)

c) Xét \(y = \frac{{2x + 1}}{{x - 2}}\) trên đoạn [3;7]

\(y' = \frac{{ - 5}}{{{{(x - 2)}^2}}} < 0\forall x \in [3;7]\)

Bảng biến thiên:

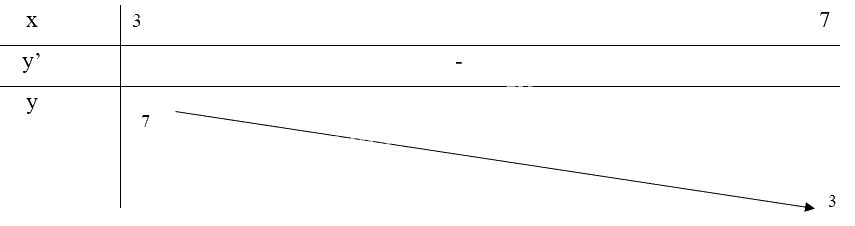
Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo 4

Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[3;7]} y = y(3) = 7\) và \(\mathop {\min }\limits_{[3;7]} y = y(7) = 3\)

d) Xét \(y = \sin 2x\) trên đoạn \([0;\frac{{7\pi }}{{12}}]\)

\(y' = 2\cos 2x = 0 \Leftrightarrow 2x = \frac{\pi }{2} + k\pi \Leftrightarrow x = \frac{\pi }{4} + \frac{{k\pi }}{2}(k \in \mathbb{Z})\)

Ta có: \(x \in [0;\frac{{7\pi }}{{12}}] \Rightarrow k = 0 \Rightarrow x = \frac{\pi }{4}\)

Bảng biến thiên:

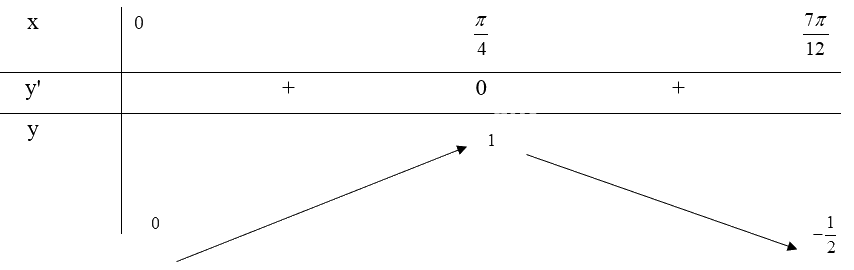
Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo 5

Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[0;\frac{{7\pi }}{{12}}]} y = y(\frac{\pi }{4}) = 1\) và \(\mathop {\min }\limits_{[0;\frac{{7\pi }}{{12}}]} y = y(\frac{{7\pi }}{{12}}) = - \frac{1}{2}\)

Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu

Bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 12, giúp học sinh củng cố kiến thức về giới hạn của hàm số. Dưới đây là hướng dẫn giải chi tiết bài tập này, giúp bạn hiểu rõ phương pháp và tự tin làm bài tập.

Nội dung bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Bài tập yêu cầu tính giới hạn của hàm số tại một điểm cho trước. Để giải bài tập này, bạn cần nắm vững các kiến thức về:

Khái niệm giới hạn của hàm số
Các định lý về giới hạn
Các phương pháp tính giới hạn (ví dụ: phương pháp chia, phương pháp nhân liên hợp)

Lời giải chi tiết bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Để giải bài tập này, chúng ta sẽ sử dụng các kiến thức và phương pháp đã nêu ở trên. Dưới đây là các bước giải cụ thể:

Xác định hàm số và điểm cần tính giới hạn.
Kiểm tra xem có thể áp dụng trực tiếp các định lý về giới hạn hay không.
Nếu không, sử dụng các phương pháp tính giới hạn phù hợp.
Thực hiện các phép tính và rút gọn biểu thức.
Kết luận giá trị của giới hạn.

Ví dụ, giả sử bài tập yêu cầu tính lim_x→2 (x² - 4) / (x - 2). Chúng ta có thể giải bài tập này như sau:

Hàm số là (x² - 4) / (x - 2) và điểm cần tính giới hạn là x = 2.
Nếu thay x = 2 trực tiếp vào hàm số, ta được 0/0, là một dạng vô định.
Chúng ta có thể phân tích tử số thành nhân tử: x² - 4 = (x - 2)(x + 2).
Khi đó, hàm số trở thành (x - 2)(x + 2) / (x - 2).
Rút gọn biểu thức, ta được x + 2.
Tính giới hạn: lim_x→2 (x + 2) = 4.
Vậy, giới hạn của hàm số tại x = 2 là 4.

Mẹo giải bài tập về giới hạn

Để giải các bài tập về giới hạn một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:

Nắm vững các định lý về giới hạn.
Luyện tập thường xuyên để làm quen với các phương pháp tính giới hạn.
Sử dụng máy tính bỏ túi để kiểm tra kết quả.
Tham khảo các tài liệu tham khảo và bài giải trên mạng.

Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín

Tusach.vn là một website cung cấp tài liệu học tập Toán 12 uy tín, với đầy đủ các bài giải, đáp án, và hướng dẫn chi tiết. Chúng tôi luôn cập nhật những thông tin mới nhất và cung cấp cho bạn những tài liệu chất lượng nhất. Hãy truy cập Tusach.vn để học tập và ôn luyện Toán 12 hiệu quả!

Hy vọng với hướng dẫn chi tiết này, bạn đã hiểu rõ cách giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo. Chúc bạn học tập tốt!

Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu

Nội dung bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Lời giải chi tiết bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Mẹo giải bài tập về giới hạn

Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN