Giải bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Xét một chất điểm chuyển động dọc theo trục (Ox). Toạ độ của chất điểm tại thời điểm (t) được xác định bởi hàm số (x(t) = {t^3} - 6{t^2} + 9t) với (t ge 0). Khi đó (x'(t)) là vận tốc của chất điểm tại thời điểm (t), kí hiệu (v(t)); (v'(t)) là gia tốc chuyển động của chất điểm tại thời điểm (t), kí hiệu (a(t)). a) Tìm các hàm (v(t))và (a(t)) b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
Đề bài
Xét một chất điểm chuyển động dọc theo trục \(Ox\). Toạ độ của chất điểm tại thời điểm \(t\) được xác định bởi hàm số \(x(t) = {t^3} - 6{t^2} + 9t\) với \(t \ge 0\). Khi đó \(x'(t)\) là vận tốc của chất điểm tại thời điểm \(t\), kí hiệu \(v(t)\); \(v'(t)\) là gia tốc chuyển động của chất điểm tại thời điểm \(t\), kí hiệu \(a(t)\). a) Tìm các hàm \(v(t)\)và \(a(t)\)b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính đạo hàm, xét dấu đạo hàm
Lời giải chi tiết
a) \(v(t) = x'(t) = 3{t^2} - 12t + 9\)
\(a(t) = v'(t) = 6t - 12\)
b) Tập xác định: \(D = [0; + \infty ]\)
\(a(t) = 0 \Leftrightarrow t = 2\)
Bảng biến thiên:
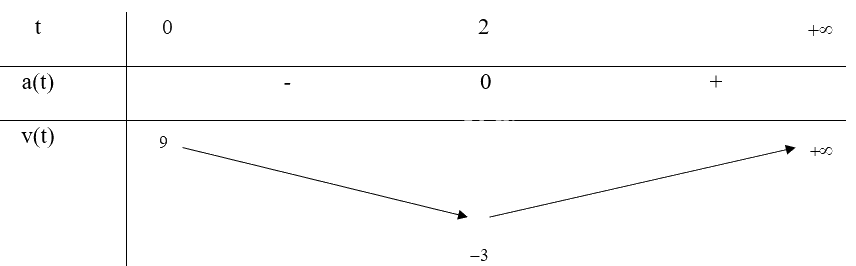
Vậy trong khoảng từ t = 0 đến t = 2 thì vận tốc của chất điểm giảm, từ t = 2 trở đi thì vận tốc của chất điểm tăng
Giải bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Đây là một phần kiến thức nền tảng quan trọng, giúp học sinh hiểu rõ hơn về sự biến đổi của hàm số khi x tiến tới một giá trị nhất định. Việc nắm vững kiến thức này không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là bước đệm quan trọng cho các kiến thức nâng cao hơn trong chương trình Toán 12.
Nội dung bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập 6 yêu cầu học sinh tính giới hạn của hàm số tại một điểm cho trước. Để giải bài tập này, học sinh cần nắm vững các quy tắc tính giới hạn, bao gồm:
- Quy tắc giới hạn của một tổng: lim (f(x) + g(x)) = lim f(x) + lim g(x)
- Quy tắc giới hạn của một tích: lim (f(x) * g(x)) = lim f(x) * lim g(x)
- Quy tắc giới hạn của một thương: lim (f(x) / g(x)) = lim f(x) / lim g(x) (với lim g(x) ≠ 0)
- Các giới hạn đặc biệt: lim (sin x / x) = 1 (khi x → 0), lim (1 - cos x) / x = 0 (khi x → 0)
Lời giải chi tiết bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, Tusach.vn xin trình bày lời giải chi tiết như sau:
Đề bài: Tính các giới hạn sau:
- lim (2x + 1) khi x → 2
- lim (x2 - 4) / (x - 2) khi x → 2
- lim (√(x + 3) - 2) / (x - 1) khi x → 1
Giải:
- lim (2x + 1) khi x → 2 = 2 * 2 + 1 = 5
- lim (x2 - 4) / (x - 2) khi x → 2 = lim (x - 2)(x + 2) / (x - 2) = lim (x + 2) = 2 + 2 = 4
- lim (√(x + 3) - 2) / (x - 1) khi x → 1 = lim (√(x + 3) - 2) / (x - 1) * (√(x + 3) + 2) / (√(x + 3) + 2) = lim (x + 3 - 4) / ((x - 1)(√(x + 3) + 2)) = lim (x - 1) / ((x - 1)(√(x + 3) + 2)) = lim 1 / (√(x + 3) + 2) = 1 / (√(1 + 3) + 2) = 1 / 4
Mẹo giải bài tập về giới hạn
Để giải các bài tập về giới hạn một cách hiệu quả, các em học sinh có thể tham khảo một số mẹo sau:
- Phân tích hàm số: Xác định dạng của hàm số và các điểm gián đoạn.
- Sử dụng các quy tắc tính giới hạn: Áp dụng các quy tắc tính giới hạn một cách linh hoạt.
- Biến đổi đại số: Sử dụng các phép biến đổi đại số để đơn giản hóa biểu thức.
- Sử dụng định lý giới hạn: Áp dụng định lý giới hạn để tính giới hạn của các hàm số phức tạp.
Tusach.vn – Đồng hành cùng học sinh trên con đường chinh phục Toán học
Tusach.vn luôn đồng hành cùng các em học sinh trong quá trình học tập và rèn luyện môn Toán. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!