Lý thuyết Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm Toán 12 Chân trời sáng tạo
Tổng quan nội dung
Lý thuyết Khoảng biến thiên và khoảng tứ phân vị Toán 12
Trong chương trình Toán 12 Chân trời sáng tạo, việc nắm vững lý thuyết về khoảng biến thiên và khoảng tứ phân vị là vô cùng quan trọng để hiểu rõ hơn về sự phân tán của dữ liệu trong thống kê. Bài viết này sẽ cung cấp một cách đầy đủ và dễ hiểu về các khái niệm này.
Chúng ta sẽ cùng nhau khám phá định nghĩa, công thức tính toán và các ví dụ minh họa cụ thể để bạn có thể áp dụng vào giải các bài tập một cách hiệu quả.
Bài 1. Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm 1. Khoảng biến thiên
1. Khoảng biến thiên
a) Định nghĩa
Khoảng biến thiên, kí hiệu R, của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu. \(R = {u_{k + 1}} - {u_1}\) |
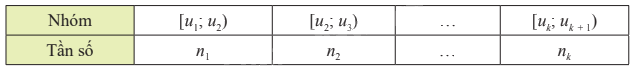
b) Ý nghĩa
- Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc và có thể dùng để đo mức độ phân tán của mẫu số liệu
- Khoảng biến thiên chưa phản ánh đầy đủ mức độ phân tán của phần lớn các số liệu. Hơn nữa giá trị của R thường tăng vọt khi xuất hiện giá trị ngoại lệ trong mẫu số liệu. Do đó, để phản ánh mức độ phân tán của số liệu, người ta còn dùng các số đặc trưng khác
2. Khoảng tứ phân vị
a) Định nghĩa
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là: \({\Delta _Q} = {Q_3} - {Q_1}\) |
b) Ý nghĩa
b) Ý nghĩa
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ phân tán của nửa giữa mẫu số liệu.
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm càng nhỏ thì dữ liệu càng tập trung xung quanh trung vị.
- Khoảng tứ phân vị được dùng để xác định giá trị ngoại lệ trong mẫu số liệu. Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu \(x > {Q_3} + 1,5\Delta Q\) hoặc \(x < {Q_1} - 1,5\Delta Q\).
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm không bị ảnh hưởng nhiều bởi các giá trị ngoại lệ trong mẫu số liệu.
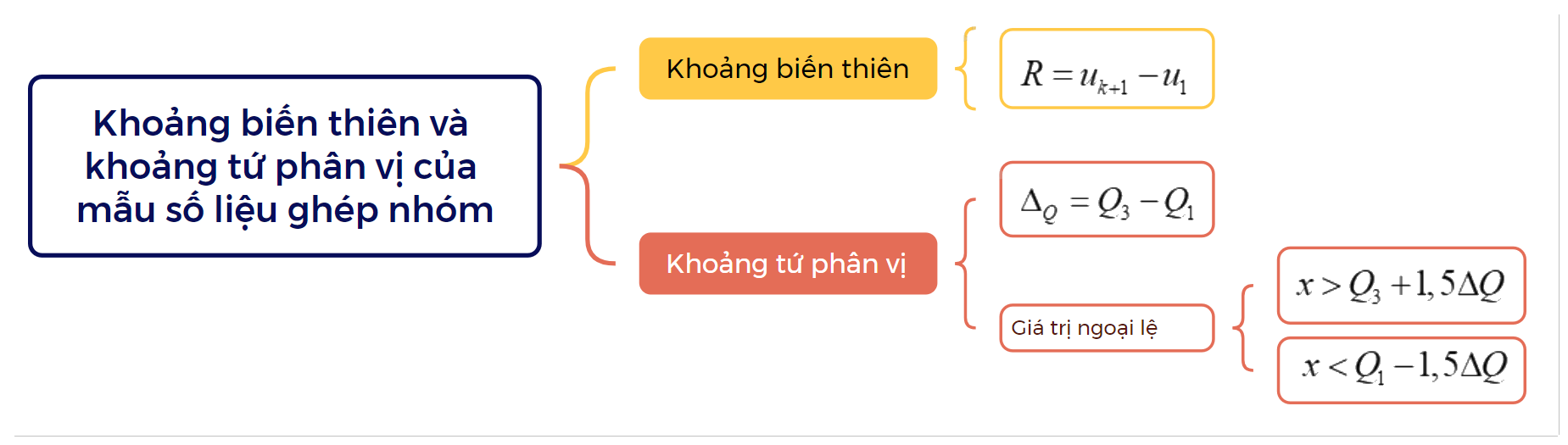
Lý Thuyết Khoảng Biến Thiên và Khoảng Tứ Phân Vị Toán 12 Chân Trời Sáng Tạo
Trong thống kê, việc đo lường mức độ phân tán của một tập dữ liệu là một yếu tố quan trọng. Khoảng biến thiên (Range) và khoảng tứ phân vị (Interquartile Range - IQR) là hai đại lượng thống kê được sử dụng phổ biến để đánh giá sự biến thiên của dữ liệu. Bài viết này sẽ trình bày chi tiết về lý thuyết và cách tính toán hai đại lượng này trong chương trình Toán 12 Chân trời sáng tạo.
1. Khoảng Biến Thiên (Range)
Khoảng biến thiên là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất trong một tập dữ liệu. Nó cho biết phạm vi mà các giá trị dữ liệu trải rộng.
Công thức:
Range = Xmax - Xmin
Trong đó:
- Xmax: Giá trị lớn nhất trong tập dữ liệu
- Xmin: Giá trị nhỏ nhất trong tập dữ liệu
Ví dụ: Cho tập dữ liệu: 2, 5, 8, 11, 15. Khoảng biến thiên là 15 - 2 = 13.
2. Khoảng Tứ Phân Vị (Interquartile Range - IQR)
Khoảng tứ phân vị là hiệu giữa tứ phân vị thứ ba (Q3) và tứ phân vị thứ nhất (Q1). Nó đo lường sự phân tán của 50% dữ liệu trung tâm trong tập dữ liệu.
Các bước tính khoảng tứ phân vị:
- Sắp xếp dữ liệu theo thứ tự tăng dần.
- Tìm tứ phân vị thứ nhất (Q1): Giá trị phân chia 25% dữ liệu nhỏ nhất.
- Tìm tứ phân vị thứ ba (Q3): Giá trị phân chia 75% dữ liệu nhỏ nhất.
- Tính IQR: IQR = Q3 - Q1
Ví dụ: Cho tập dữ liệu: 3, 7, 8, 10, 12, 15, 18.
- Sắp xếp: 3, 7, 8, 10, 12, 15, 18
- Q1 = 7
- Q3 = 15
- IQR = 15 - 7 = 8
3. Khoảng Biến Thiên và Khoảng Tứ Phân Vị của Mẫu Số Liệu Ghép Nhóm
Khi dữ liệu được biểu diễn dưới dạng bảng tần số (mẫu số liệu ghép nhóm), việc tính khoảng biến thiên và khoảng tứ phân vị sẽ phức tạp hơn.
a. Khoảng biến thiên:
Range = (Xmax + h/2) - (Xmin - h/2)
Trong đó:
- Xmax: Giới hạn trên của nhóm chứa giá trị lớn nhất
- Xmin: Giới hạn dưới của nhóm chứa giá trị nhỏ nhất
- h: Khoảng lớp
b. Khoảng tứ phân vị:
Việc tính Q1 và Q3 trong mẫu số liệu ghép nhóm đòi hỏi phải sử dụng công thức nội suy.
Q1 = L1 + ( (N/4) - cf1 ) / f1 * h
Q3 = L3 + ( (3N/4) - cf3 ) / f3 * h
Trong đó:
- L1: Giới hạn dưới của nhóm chứa Q1
- L3: Giới hạn dưới của nhóm chứa Q3
- N: Tổng tần số
- cf1: Tần số tích lũy của nhóm trước nhóm chứa Q1
- cf3: Tần số tích lũy của nhóm trước nhóm chứa Q3
- f1: Tần số của nhóm chứa Q1
- f3: Tần số của nhóm chứa Q3
- h: Khoảng lớp
4. Ứng Dụng của Khoảng Biến Thiên và Khoảng Tứ Phân Vị
Khoảng biến thiên và khoảng tứ phân vị được sử dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
- Thống kê mô tả: Tóm tắt và mô tả các đặc điểm chính của một tập dữ liệu.
- Phân tích dữ liệu: Xác định các giá trị ngoại lệ và đánh giá sự phân tán của dữ liệu.
- Kiểm soát chất lượng: Theo dõi và kiểm soát sự biến thiên trong quá trình sản xuất.
Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và đầy đủ về lý thuyết Khoảng biến thiên và khoảng tứ phân vị trong chương trình Toán 12 Chân trời sáng tạo. Hãy luyện tập thêm với các bài tập để nắm vững kiến thức này nhé!