Giải mục 4 trang 30,31,32 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 4 trang 30, 31, 32 SGK Toán 12 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 4 trang 30, 31, 32 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài học, tự tin giải quyết các bài tập và đạt kết quả cao trong môn Toán.
Khảo sát hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}(a \ne 0,m \ne 0\), đa thức tử không chia hết cho đa thức mẫu)
- TH3
Trả lời câu hỏi Thực hành 3 trang 32 SGK Toán 12 Chân trời sáng tạo
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = x - \frac{1}{x}\)
b) \(y = - x + 2 - \frac{1}{{x + 1}}\)
c) \(y = \frac{{ - {x^2} - x + 2}}{{x + 1}}\)
Phương pháp giải:
Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu, cực trị (nếu có) của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và các đường tiệm cận của đồ thị hàm số (nếu có).
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
Lời giải chi tiết:
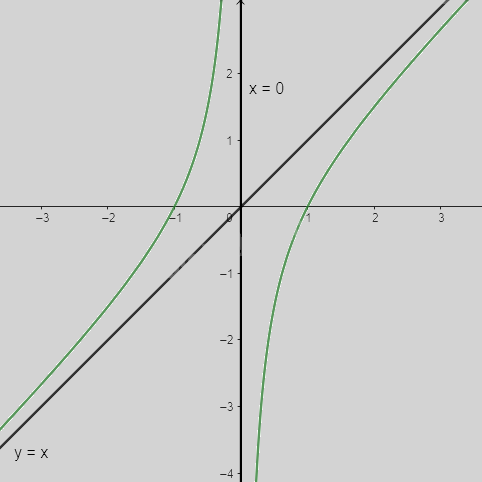
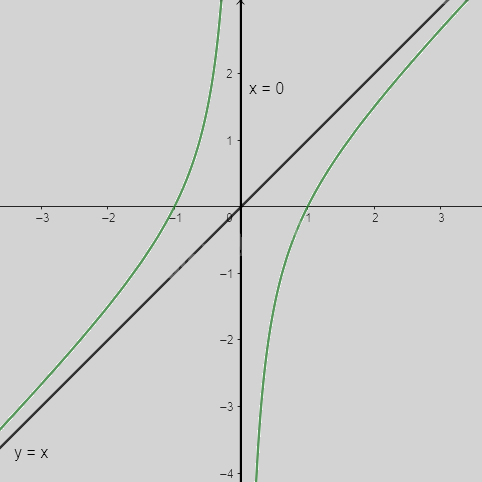
a) \(y = x - \frac{1}{x}\)
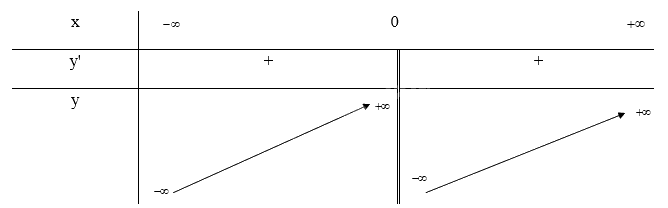
Tập xác định: \(D = \mathbb{R}\backslash \{ 0\} \)
- Chiều biến thiên:
\(y' = 1 + \frac{1}{{{x^2}}} \ge 0\forall x \in D\) nên hàm số đồng biến trên D
- Giới hạn và tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } (x - \frac{1}{x}) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } (x - \frac{1}{x}) = - \infty \)
\(a = \mathop {\lim }\limits_{x \to + \infty } (1 - \frac{1}{{{x^2}}}) = 1;b = \mathop {\lim }\limits_{x \to + \infty } (x - \frac{1}{x} - x) = 0\) nên y = x là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} (x - \frac{1}{x}) = - \infty ;\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} (x - \frac{1}{x}) = + \infty \) nên x = 0 là tiệm cận đứng của đồ thị hàm số
- Bảng biến thiên:
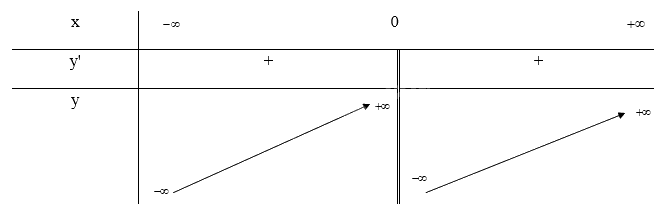 Ta có: \(y = 0 \Leftrightarrow x - \frac{1}{x} = 0 \Leftrightarrow x = 1\)
Ta có: \(y = 0 \Leftrightarrow x - \frac{1}{x} = 0 \Leftrightarrow x = 1\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (1; 0)
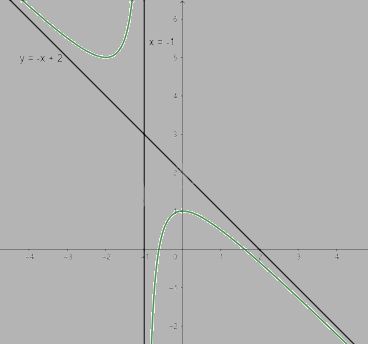
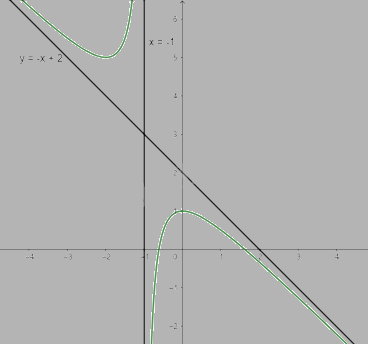
b) \(y = - x + 2 - \frac{1}{{x + 1}}\)
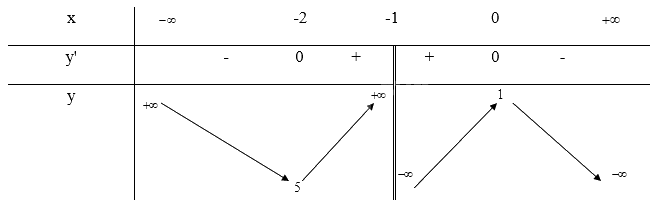
Tập xác định: \(D = \mathbb{R}\backslash \{ - 1\} \)
- Chiều biến thiên:
\(y' = - 1 + \frac{1}{{{{(x + 1)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 0\end{array} \right.\)
Trên các khoảng (\( - \infty \); -2), (0; \( + \infty \)) thì y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó. Trên khoảng (-2; -1) và (-1; 0) thì y' > 0 nên hàm số đồng biến trên khoảng đó.
- Giới hạn và tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } ( - x + 2 - \frac{1}{{x + 1}}) = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } ( - x + 2 - \frac{1}{{x + 1}}) = + \infty \)
\(a = \mathop {\lim }\limits_{x \to + \infty } ( - 1 + \frac{2}{x} - \frac{1}{{{x^2} + x}}) = - 1;b = \mathop {\lim }\limits_{x \to + \infty } ( - x + 2 - \frac{1}{{x + 1}} + x) = 2\) nên y = -x + 2 là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} ( - x + 2 - \frac{1}{{x + 1}}) = - \infty ;\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} ( - x + 2 - \frac{1}{{x + 1}}) = + \infty \) nên x = -1 là tiệm cận đứng của đồ thị hàm số
- Bảng biến thiên:
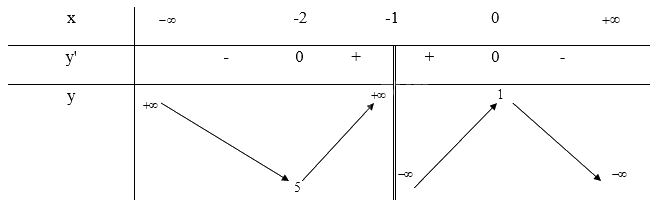
Khi x = 0 thì y = 1 nên (0;1) là giao điểm của y với trục Oy
Ta có: \(y = 0 \Leftrightarrow - x + 2 - \frac{1}{{x + 1}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{1 - \sqrt 5 }}{2}\\x = \frac{{1 + \sqrt 5 }}{2}\end{array} \right.\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (\(\frac{{1 - \sqrt 5 }}{2}\); 0) và (\(\frac{{1 + \sqrt 5 }}{2}\);0)
TH3
Trả lời câu hỏi Thực hành 3 trang 32 SGK Toán 12 Chân trời sáng tạo
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = x - \frac{1}{x}\)
b) \(y = - x + 2 - \frac{1}{{x + 1}}\)
c) \(y = \frac{{ - {x^2} - x + 2}}{{x + 1}}\)
Phương pháp giải:
Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu, cực trị (nếu có) của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và các đường tiệm cận của đồ thị hàm số (nếu có).
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
Lời giải chi tiết:
a) \(y = x - \frac{1}{x}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 0\} \)
- Chiều biến thiên:
\(y' = 1 + \frac{1}{{{x^2}}} \ge 0\forall x \in D\) nên hàm số đồng biến trên D
- Giới hạn và tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } (x - \frac{1}{x}) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } (x - \frac{1}{x}) = - \infty \)
\(a = \mathop {\lim }\limits_{x \to + \infty } (1 - \frac{1}{{{x^2}}}) = 1;b = \mathop {\lim }\limits_{x \to + \infty } (x - \frac{1}{x} - x) = 0\) nên y = x là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} (x - \frac{1}{x}) = - \infty ;\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} (x - \frac{1}{x}) = + \infty \) nên x = 0 là tiệm cận đứng của đồ thị hàm số
- Bảng biến thiên:
 Ta có: \(y = 0 \Leftrightarrow x - \frac{1}{x} = 0 \Leftrightarrow x = 1\)
Ta có: \(y = 0 \Leftrightarrow x - \frac{1}{x} = 0 \Leftrightarrow x = 1\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (1; 0)
b) \(y = - x + 2 - \frac{1}{{x + 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ - 1\} \)
- Chiều biến thiên:
\(y' = - 1 + \frac{1}{{{{(x + 1)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 0\end{array} \right.\)
Trên các khoảng (\( - \infty \); -2), (0; \( + \infty \)) thì y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó. Trên khoảng (-2; -1) và (-1; 0) thì y' > 0 nên hàm số đồng biến trên khoảng đó.
- Giới hạn và tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } ( - x + 2 - \frac{1}{{x + 1}}) = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } ( - x + 2 - \frac{1}{{x + 1}}) = + \infty \)
\(a = \mathop {\lim }\limits_{x \to + \infty } ( - 1 + \frac{2}{x} - \frac{1}{{{x^2} + x}}) = - 1;b = \mathop {\lim }\limits_{x \to + \infty } ( - x + 2 - \frac{1}{{x + 1}} + x) = 2\) nên y = -x + 2 là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} ( - x + 2 - \frac{1}{{x + 1}}) = - \infty ;\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} ( - x + 2 - \frac{1}{{x + 1}}) = + \infty \) nên x = -1 là tiệm cận đứng của đồ thị hàm số
- Bảng biến thiên:
Khi x = 0 thì y = 1 nên (0;1) là giao điểm của y với trục Oy
Ta có: \(y = 0 \Leftrightarrow - x + 2 - \frac{1}{{x + 1}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{1 - \sqrt 5 }}{2}\\x = \frac{{1 + \sqrt 5 }}{2}\end{array} \right.\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (\(\frac{{1 - \sqrt 5 }}{2}\); 0) và (\(\frac{{1 + \sqrt 5 }}{2}\);0)
Giải mục 4 trang 30, 31, 32 SGK Toán 12 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 4 của SGK Toán 12 tập 1 chương trình Chân trời sáng tạo tập trung vào việc nghiên cứu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng trong giải tích, mở đầu cho việc học về đạo hàm và tích phân. Việc nắm vững kiến thức về giới hạn hàm số sẽ giúp học sinh hiểu rõ hơn về sự biến đổi của hàm số khi biến số tiến tới một giá trị nhất định.
Nội dung chính của Mục 4
- Khái niệm giới hạn của hàm số tại một điểm: Học sinh sẽ được làm quen với định nghĩa giới hạn của hàm số khi x tiến tới một giá trị cụ thể.
- Tính chất của giới hạn hàm số: Tìm hiểu các tính chất cơ bản của giới hạn, như giới hạn của tổng, hiệu, tích, thương và lũy thừa.
- Các dạng giới hạn thường gặp: Luyện tập giải các bài toán giới hạn với các dạng khác nhau, bao gồm giới hạn vô cùng, giới hạn tại vô cùng.
- Ứng dụng của giới hạn hàm số: Khám phá các ứng dụng thực tế của giới hạn hàm số trong việc giải quyết các bài toán liên quan đến sự biến đổi của hàm số.
Giải chi tiết các bài tập trang 30, 31, 32
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 4 trang 30, 31, 32 SGK Toán 12 tập 1 Chân trời sáng tạo:
Bài 1: (Trang 30)
Đề bài: Tính giới hạn sau: lim (x→2) (x^2 - 4) / (x - 2)
Lời giải:
- Ta có: (x^2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2)
- Khi x ≠ 2, ta có thể rút gọn biểu thức thành: x + 2
- Vậy, lim (x→2) (x^2 - 4) / (x - 2) = lim (x→2) (x + 2) = 2 + 2 = 4
Bài 2: (Trang 31)
Đề bài: Tính giới hạn sau: lim (x→∞) (2x + 1) / (x - 3)
Lời giải:
Chia cả tử và mẫu cho x, ta được:
lim (x→∞) (2 + 1/x) / (1 - 3/x) = (2 + 0) / (1 - 0) = 2
Bài 3: (Trang 32)
Đề bài: ... (Tiếp tục giải các bài tập còn lại tương tự)
Mẹo giải bài tập về giới hạn hàm số
- Phân tích và đơn giản hóa biểu thức: Sử dụng các phép biến đổi đại số để đơn giản hóa biểu thức, loại bỏ các yếu tố gây khó khăn trong việc tính giới hạn.
- Sử dụng các định lý về giới hạn: Áp dụng các định lý về giới hạn của tổng, hiệu, tích, thương và lũy thừa để tính giới hạn của các biểu thức phức tạp.
- Sử dụng các dạng giới hạn đặc biệt: Nhận biết và sử dụng các dạng giới hạn đặc biệt, như giới hạn của (sin x) / x khi x → 0.
- Kiểm tra lại kết quả: Sau khi tính giới hạn, hãy kiểm tra lại kết quả bằng cách thay các giá trị gần với giá trị giới hạn vào biểu thức để đảm bảo tính chính xác.
Tusach.vn – Đồng hành cùng bạn học Toán 12
Tusach.vn tự hào là một nguồn tài liệu học tập Toán 12 uy tín và chất lượng. Chúng tôi cung cấp đầy đủ lời giải chi tiết, bài tập trắc nghiệm và các tài liệu hỗ trợ học tập khác để giúp các em học sinh đạt kết quả tốt nhất trong môn Toán. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!