Giải mục 1 trang 41,42,43 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 41,42,43 SGK Toán 12 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 41, 42, 43 sách giáo khoa Toán 12 tập 1 chương trình Chân trời sáng tạo. tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, từ đó áp dụng kiến thức vào các bài tập khác một cách hiệu quả.
Vectơ trong không gian
KP1
Trả lời câu hỏi Khám phá 1 trang 41 SGK Toán 12 Chân trời sáng tạo
Nhắc lại định nghĩa vectơ trong mặt phẳng. Có thể định nghĩa vectơ trong không gian như đã định nghĩa vectơ trong mặt phẳng không?
Phương pháp giải:
Nhớ lại định nghĩa
Lời giải chi tiết:
- Vecto trong mặt phẳng tọa độ là một đoạn thẳng có hướng, có điểm đầu và cuối, nằm trong hệ trục tọa độ Oxy với tọa độ là , trong đó là hoành độ và là tung độ
- Vecto trong không gian có thể được định nghĩa tương tự như vecto trong mặt phẳng
TH1
Trả lời câu hỏi Thực hành 1 trang 42 SGK Toán 12 Chân trời sáng tạo
Trong Khởi động, tìm vectơ biểu diễn độ dịch chuyển tín hiệu vô tuyến từ vị trí A của máy bay đến vị trí S của trạm kiểm soát
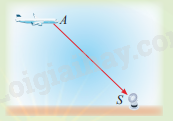
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Vectơ biểu diễn độ dịch chuyển tín hiệu vô tuyến từ vị trí A của máy bay đến vị trí S của trạm kiểm soát là \(\overrightarrow {AS} \)
TH2
Trả lời câu hỏi Thực hành 2 trang 42 SGK Toán 12 Chân trời sáng tạo
Cho hình chóp tứ giác đều S.ABCD.
a) Chỉ ra các vectơ có điểm đầu là S và điểm cuối là các đỉnh của đa giác đáy
b) Tìm các vectơ có độ dài bằng độ dài của vectơ \(\overrightarrow {SA} \)
c) Tìm các vectơ đối của vectơ \(\overrightarrow {CB} \)
Phương pháp giải:
Vẽ hình rồi quan sát
Lời giải chi tiết:
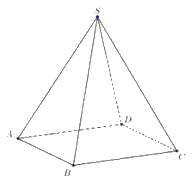
a) Các vecto: \(\overrightarrow {SA} ;\overrightarrow {SB} \overrightarrow {;SC} \overrightarrow {;SD} \)
b) Các vectơ có độ dài bằng độ dài của vectơ \(\overrightarrow {SA} \): \(\overrightarrow {SB} \overrightarrow {;SC} \overrightarrow {;SD} \)
c) Các vectơ đối của vectơ \(\overrightarrow {CB} \): \(\overrightarrow {AD} \)
VD1
Trả lời câu hỏi Vận dụng 1 trang 43 SGK Toán 12 Chân trời sáng tạo
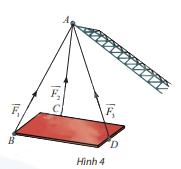
Trong Hình 4, cho biết ba vectơ \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} \) biểu diễn lực căng của các sợi dây cáp AB, AC, AD tác dụng lên vật nặng. Giá của ba vectơ này có cùng nằm trên một mặt phẳng không?
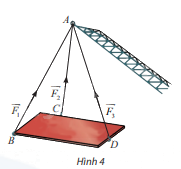
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Giá của 3 vecto \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} \) không cùng nằm trên một mặt phẳng
- KP1
- TH1
- TH2
- VD1
Trả lời câu hỏi Khám phá 1 trang 41 SGK Toán 12 Chân trời sáng tạo
Nhắc lại định nghĩa vectơ trong mặt phẳng. Có thể định nghĩa vectơ trong không gian như đã định nghĩa vectơ trong mặt phẳng không?
Phương pháp giải:
Nhớ lại định nghĩa
Lời giải chi tiết:
- Vecto trong mặt phẳng tọa độ là một đoạn thẳng có hướng, có điểm đầu và cuối, nằm trong hệ trục tọa độ Oxy với tọa độ là , trong đó là hoành độ và là tung độ
- Vecto trong không gian có thể được định nghĩa tương tự như vecto trong mặt phẳng
Trả lời câu hỏi Thực hành 1 trang 42 SGK Toán 12 Chân trời sáng tạo
Trong Khởi động, tìm vectơ biểu diễn độ dịch chuyển tín hiệu vô tuyến từ vị trí A của máy bay đến vị trí S của trạm kiểm soát
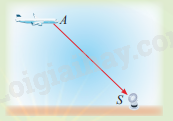
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Vectơ biểu diễn độ dịch chuyển tín hiệu vô tuyến từ vị trí A của máy bay đến vị trí S của trạm kiểm soát là \(\overrightarrow {AS} \)
Trả lời câu hỏi Thực hành 2 trang 42 SGK Toán 12 Chân trời sáng tạo
Cho hình chóp tứ giác đều S.ABCD.
a) Chỉ ra các vectơ có điểm đầu là S và điểm cuối là các đỉnh của đa giác đáy
b) Tìm các vectơ có độ dài bằng độ dài của vectơ \(\overrightarrow {SA} \)
c) Tìm các vectơ đối của vectơ \(\overrightarrow {CB} \)
Phương pháp giải:
Vẽ hình rồi quan sát
Lời giải chi tiết:
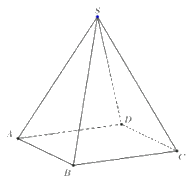
a) Các vecto: \(\overrightarrow {SA} ;\overrightarrow {SB} \overrightarrow {;SC} \overrightarrow {;SD} \)
b) Các vectơ có độ dài bằng độ dài của vectơ \(\overrightarrow {SA} \): \(\overrightarrow {SB} \overrightarrow {;SC} \overrightarrow {;SD} \)
c) Các vectơ đối của vectơ \(\overrightarrow {CB} \): \(\overrightarrow {AD} \)
Trả lời câu hỏi Vận dụng 1 trang 43 SGK Toán 12 Chân trời sáng tạo
Trong Hình 4, cho biết ba vectơ \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} \) biểu diễn lực căng của các sợi dây cáp AB, AC, AD tác dụng lên vật nặng. Giá của ba vectơ này có cùng nằm trên một mặt phẳng không?
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Giá của 3 vecto \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} \) không cùng nằm trên một mặt phẳng
Giải mục 1 trang 41,42,43 SGK Toán 12 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 1 trang 41, 42, 43 SGK Toán 12 tập 1 Chân trời sáng tạo tập trung vào việc ôn tập về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Đây là một phần kiến thức nền tảng quan trọng, đóng vai trò then chốt trong việc giải quyết các bài toán phức tạp hơn ở các chương sau. Bài viết này sẽ cung cấp lời giải chi tiết từng bài tập, kèm theo các lưu ý quan trọng để giúp các em hiểu sâu sắc hơn về nội dung bài học.
Nội dung chính của Mục 1
- Ôn tập về đạo hàm: Định nghĩa đạo hàm, các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
- Ứng dụng của đạo hàm: Khảo sát hàm số (xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn), giải phương trình, bất phương trình.
- Bài tập áp dụng: Các bài tập vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giải chi tiết các bài tập
Bài 1: Tính đạo hàm của các hàm số sau
(Ví dụ: f(x) = x3 - 2x2 + 5x - 1)
Lời giải: f'(x) = 3x2 - 4x + 5
Bài 2: Tìm cực trị của hàm số sau
(Ví dụ: y = x3 - 3x2 + 2)
Lời giải:
- Tính đạo hàm y' = 3x2 - 6x
- Giải phương trình y' = 0 để tìm các điểm cực trị: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Lập bảng biến thiên để xác định cực đại, cực tiểu.
Bài 3: Khảo sát hàm số sau
(Ví dụ: y = (x-1)/(x+1)
Lời giải:
- Xác định tập xác định: x ≠ -1
- Tính đạo hàm y' = -2/(x+1)2
- Nhận xét: y' < 0 với mọi x ≠ -1, do đó hàm số nghịch biến trên các khoảng (-∞, -1) và (-1, +∞).
- Không có cực trị.
- Tiệm cận đứng: x = -1
- Tiệm cận ngang: y = 1
Lưu ý quan trọng khi giải bài tập
Để giải quyết hiệu quả các bài tập về đạo hàm và ứng dụng của đạo hàm, các em cần:
- Nắm vững định nghĩa và các quy tắc tính đạo hàm.
- Hiểu rõ các bước khảo sát hàm số.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra kết quả.
Tusach.vn – Đồng hành cùng bạn học Toán 12
tusach.vn cam kết cung cấp lời giải chính xác, dễ hiểu và đầy đủ cho tất cả các bài tập trong SGK Toán 12 tập 1 Chân trời sáng tạo. Ngoài ra, chúng tôi còn cung cấp nhiều tài liệu học tập hữu ích khác như bài giảng, đề thi thử, và các bài viết hướng dẫn giải bài tập. Hãy truy cập tusach.vn ngay hôm nay để khám phá và nâng cao kiến thức Toán 12 của bạn!
| Chương | Bài | Link |
|---|---|---|
| 1 | Mục 1 | tusach.vn/giai-toan-12-chan-troi-sang-tao-muc-1 |