Đề bài
Cho biết bốn đoạn thẳng nối từ một đỉnh của tứ diện đến trọng tâm mặt đối diện luôn cắt nhau tại một điểm gọi là trọng tâm của tứ diện đó.
Một phân tử metan CH4 được cấu tạo bởi bốn nguyên tử hydrogen ở các đỉnh của một tứ diện đều và một nguyên tử carbon ở trọng tâm của tứ diện.
Góc liên kết là góc tạo bởi liên kết H–C–H là góc giữa các đường nối nguyên tử carbon với hai trong số các nguyên tử hydrogen. Chứng minh rằng góc liên kết này gần bằng \(109,5^\circ \)
Phương pháp giải - Xem chi tiết
Dựng một hệ trục tọa độ theo đề và dùng công thức tích vô hướng giữa 2 vecto để tìm góc liên kết
Lời giải chi tiết
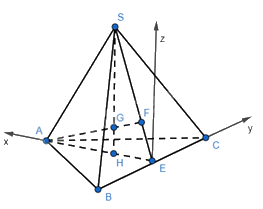
Từ hình vẽ ta thấy góc liên kết là góc \((\overrightarrow {GA} ,\overrightarrow {GS} )\)
Ta có: \(AE \bot BC\), \(SH \bot (ABC) \Rightarrow \left\{ \begin{array}{l}SH \bot AE\\SH \bot BC\end{array} \right.\) nên ta có hệ trục tọa độ như hình với với E trùng với gốc tọa độ O
Giả sử các cạnh của tứ diện có độ dài là a
Ta có: \(SE = AE = \sqrt {A{B^2} - B{E^2}} = \sqrt {{a^2} - {{(\frac{a}{2})}^2}} = \frac{{a\sqrt 3 }}{2} \Rightarrow A(\frac{{a\sqrt 3 }}{2};0;0)\)
\(HE = \frac{{AE}}{3} = \frac{{a\sqrt 3 }}{6} \Rightarrow H(\frac{{a\sqrt 3 }}{6};0;0)\)
\(SH = \sqrt {S{E^2} - H{E^2}} = \sqrt {{{(\frac{{a\sqrt 3 }}{2})}^2} - {{(\frac{{a\sqrt 3 }}{6})}^2}} = \frac{{a\sqrt 6 }}{3} \Rightarrow S(\frac{{a\sqrt 3 }}{6};0;\frac{{a\sqrt 6 }}{3})\)
Lại có: \(\frac{{FE}}{{SE}} = \frac{{HE}}{{AE}} = \frac{1}{3} \Rightarrow FH//SA\) và AF cắt SH tại G nên \(\frac{{GH}}{{GS}} = \frac{{GF}}{{GE}} = \frac{{FH}}{{SA}} = \frac{{HE}}{{AE}} = \frac{1}{3}\)
\( \Rightarrow GH = \frac{1}{4}SH = \frac{1}{4}.\frac{{a\sqrt 6 }}{3} = \frac{{a\sqrt 6 }}{{12}} \Rightarrow G(\frac{{a\sqrt 3 }}{6};0;\frac{{a\sqrt 6 }}{{12}})\)
Do đó: \(\overrightarrow {GA} = (\frac{{a\sqrt 3 }}{3};0; - \frac{{a\sqrt 6 }}{{12}}) \Rightarrow GA = \frac{{a\sqrt 6 }}{4}\)
\(\overrightarrow {GS} = (0;0;\frac{{a\sqrt 6 }}{4}) \Rightarrow GS = \frac{{a\sqrt 6 }}{4}\)
Ta có: \(\cos (\overrightarrow {GA} ,\overrightarrow {GS} ) = \frac{{ - \frac{{a\sqrt 6 }}{{12}}.\frac{{a\sqrt 6 }}{4}}}{{\frac{{a\sqrt 6 }}{4}.\frac{{a\sqrt 6 }}{4}}} = - \frac{1}{3} \Rightarrow (\overrightarrow {GA} ,\overrightarrow {GS} ) \approx 109,5^\circ \)
