Giải mục 1 trang 32, 33 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 32, 33 SGK Toán 12 tập 2 - Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết mục 1 trang 32, 33 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo. Tại tusach.vn, chúng tôi luôn cố gắng cung cấp những giải pháp học tập hiệu quả nhất cho các em học sinh.
Bài viết này sẽ giúp bạn hiểu rõ các khái niệm, công thức và phương pháp giải bài tập trong mục này.
a) Cho vectơ (vec n) khác (vec 0). Qua một điểm ({M_0}) cố định trong không gian, có bao nhiêu mặt phẳng (left( alpha right)) vuông góc với giá của vectơ (vec n)?
VD1
Trả lời câu hỏi Vận dụng 1 trang 33 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {3;0;0} \right)\), \(B\left( {0;4;0} \right)\), \(C\left( {0;0;5} \right)\).
a) Tìm toạ độ của một cặp vectơ chỉ phương của mặt phẳng \(\left( {ABC} \right)\).
b) Tìm toạ độ của một vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
Phương pháp giải:
a) Chỉ ra 2 vectơ không cùng phương và có giá song song hoặc nằm trên mặt phẳng \(\left( {ABC} \right)\).
b) Chỉ ra 1 đường thẳng vuông góc với mặt phẳng \(\left( {OAB} \right)\), sau đó chọn 1 vectơ nằm trên mặt phẳng đó làm vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
Lời giải chi tiết:
a) Ta có \(\overrightarrow {AB} \left( { - 3;4;0} \right)\) và \(\overrightarrow {AC} \left( { - 3;0;5} \right)\) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {ABC} \right)\). Vậy \(\overrightarrow {AB} \left( { - 3;4;0} \right)\) và \(\overrightarrow {AC} \left( { - 3;0;5} \right)\) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {ABC} \right)\).
b) Ta thấy rằng \(A\left( {3;0;0} \right) \in Ox\), \(B\left( {0;4;0} \right) \in Oy\), \(C\left( {0;0;5} \right) \in Oz\).
Dễ dàng suy ra rằng \(OC \bot OA\) và \(OC \bot OB\), từ đó \(OC \bot \left( {OAB} \right)\).
Hơn nữa, vectơ \(\overrightarrow {OC} \left( {0;0;5} \right)\) có giá là đường thẳng \(OC\). Do đó \(\overrightarrow {OC} \left( {0;0;5} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 32 SGK Toán 12 Chân trời sáng tạo
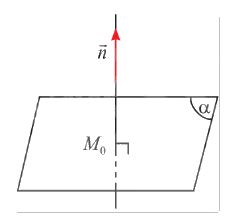
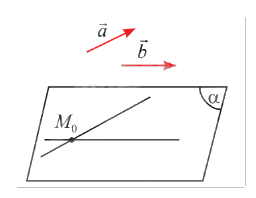
a) Cho vectơ \(\vec n\) khác \(\vec 0\). Qua một điểm \({M_0}\) cố định trong không gian, có bao nhiêu mặt phẳng \(\left( \alpha \right)\) vuông góc với giá của vectơ \(\vec n\)?
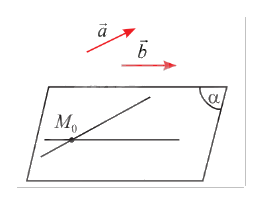
b) Cho hai vectơ \(\vec a\) và \(\vec b\) không cùng phương. Qua một điểm \({M_0}\) cố định trong không gian, có bao nhiêu mặt phẳng \(\left( \alpha \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\)?
Phương pháp giải:
Sử dụng các kiến thức về đường thẳng vuông góc mặt phẳng, đường thẳng song song với mặt phẳng đã được học ở các lớp dưới.
Lời giải chi tiết:
a) Với một điểm và một đường thẳng trong không gian, có duy nhất một mặt phẳng đi qua điểm và vuông góc với đường thẳng đó. Vậy có duy nhất một mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\) và vuông góc với giá của vectơ \(\vec n\).
b) Do hai vectơ \(\vec a\) và \(\vec b\) không cùng phương, giá của hai vectơ (lần lượt là \(a\) và \(b\)) không song song hay trùng nhau. Chọn đường thẳng \(a'\) sao cho \(a'\) song song hoặc trùng với \(a\) và \(a'\) cắt \(b\). Khi đó, có duy nhất một mặt phẳng \(\left( \beta \right)\) chứa \(a'\) và \(b\).
Nếu \({M_0} \in \left( \beta \right)\) thì mặt phẳng \(\left( \beta \right)\) là mặt phẳng duy nhất đi qua \({M_0}\) và song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).
Nếu \({M_0} \notin \left( \beta \right)\), thì trong không gian, tồn tại duy nhất mặt phẳng \(\left( \alpha \right)\) đi qua \({M_0}\) và song song với \(\left( \beta \right)\). Khi đó, \(\left( \alpha \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).
TH1
Trả lời câu hỏi Thực hành 1 trang 33 SGK Toán 12 Chân trời sáng tạo
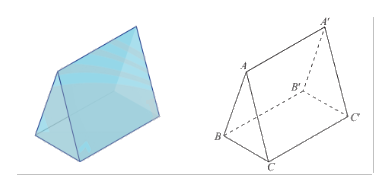
Một lăng kính có dạng hình trụ đứng có đáy là tam giác đều ở hình a được vẽ lại như hình b. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).
Phương pháp giải:
Để xác định một cặp vectơ chỉ phương của mặt phẳng \(\left( {A'B'C'} \right)\), chỉ ra hai vectơ không cùng phương và có giá song song hoặc nằm trong mặt phẳng \(\left( {A'B'C'} \right)\).
Để xác định một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\), chỉ ra một đường thẳng vuông góc với \(\left( {A'B'C'} \right)\), sau đó chọn một vectơ có giá song song hoặc trùng với đường thẳng đó.
Lời giải chi tiết:
Ta thấy rằng \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {A'B'C'} \right)\). Suy ra \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {A'B'C'} \right)\).
Do \(ABC.A'B'C'\) là lăng trụ đứng, nên ta có \(BB' \bot \left( {A'B'C'} \right)\).
Mặt khác, vectơ \(\overrightarrow {BB'} \) có giá là đường thẳng \(BB'\), do đó \(\overrightarrow {BB'} \) là một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).
- HĐ1
- VD1
- TH1
Trả lời câu hỏi Hoạt động 1 trang 32 SGK Toán 12 Chân trời sáng tạo
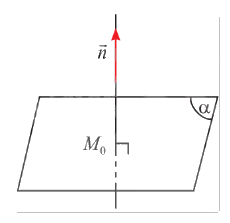
a) Cho vectơ \(\vec n\) khác \(\vec 0\). Qua một điểm \({M_0}\) cố định trong không gian, có bao nhiêu mặt phẳng \(\left( \alpha \right)\) vuông góc với giá của vectơ \(\vec n\)?
b) Cho hai vectơ \(\vec a\) và \(\vec b\) không cùng phương. Qua một điểm \({M_0}\) cố định trong không gian, có bao nhiêu mặt phẳng \(\left( \alpha \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\)?
Phương pháp giải:
Sử dụng các kiến thức về đường thẳng vuông góc mặt phẳng, đường thẳng song song với mặt phẳng đã được học ở các lớp dưới.
Lời giải chi tiết:
a) Với một điểm và một đường thẳng trong không gian, có duy nhất một mặt phẳng đi qua điểm và vuông góc với đường thẳng đó. Vậy có duy nhất một mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\) và vuông góc với giá của vectơ \(\vec n\).
b) Do hai vectơ \(\vec a\) và \(\vec b\) không cùng phương, giá của hai vectơ (lần lượt là \(a\) và \(b\)) không song song hay trùng nhau. Chọn đường thẳng \(a'\) sao cho \(a'\) song song hoặc trùng với \(a\) và \(a'\) cắt \(b\). Khi đó, có duy nhất một mặt phẳng \(\left( \beta \right)\) chứa \(a'\) và \(b\).
Nếu \({M_0} \in \left( \beta \right)\) thì mặt phẳng \(\left( \beta \right)\) là mặt phẳng duy nhất đi qua \({M_0}\) và song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).
Nếu \({M_0} \notin \left( \beta \right)\), thì trong không gian, tồn tại duy nhất mặt phẳng \(\left( \alpha \right)\) đi qua \({M_0}\) và song song với \(\left( \beta \right)\). Khi đó, \(\left( \alpha \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).
Trả lời câu hỏi Vận dụng 1 trang 33 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {3;0;0} \right)\), \(B\left( {0;4;0} \right)\), \(C\left( {0;0;5} \right)\).
a) Tìm toạ độ của một cặp vectơ chỉ phương của mặt phẳng \(\left( {ABC} \right)\).
b) Tìm toạ độ của một vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
Phương pháp giải:
a) Chỉ ra 2 vectơ không cùng phương và có giá song song hoặc nằm trên mặt phẳng \(\left( {ABC} \right)\).
b) Chỉ ra 1 đường thẳng vuông góc với mặt phẳng \(\left( {OAB} \right)\), sau đó chọn 1 vectơ nằm trên mặt phẳng đó làm vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
Lời giải chi tiết:
a) Ta có \(\overrightarrow {AB} \left( { - 3;4;0} \right)\) và \(\overrightarrow {AC} \left( { - 3;0;5} \right)\) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {ABC} \right)\). Vậy \(\overrightarrow {AB} \left( { - 3;4;0} \right)\) và \(\overrightarrow {AC} \left( { - 3;0;5} \right)\) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {ABC} \right)\).
b) Ta thấy rằng \(A\left( {3;0;0} \right) \in Ox\), \(B\left( {0;4;0} \right) \in Oy\), \(C\left( {0;0;5} \right) \in Oz\).
Dễ dàng suy ra rằng \(OC \bot OA\) và \(OC \bot OB\), từ đó \(OC \bot \left( {OAB} \right)\).
Hơn nữa, vectơ \(\overrightarrow {OC} \left( {0;0;5} \right)\) có giá là đường thẳng \(OC\). Do đó \(\overrightarrow {OC} \left( {0;0;5} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
Trả lời câu hỏi Thực hành 1 trang 33 SGK Toán 12 Chân trời sáng tạo
Một lăng kính có dạng hình trụ đứng có đáy là tam giác đều ở hình a được vẽ lại như hình b. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).
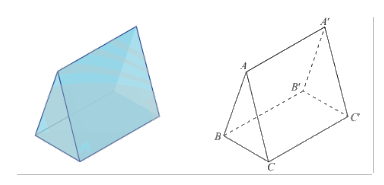
Phương pháp giải:
Để xác định một cặp vectơ chỉ phương của mặt phẳng \(\left( {A'B'C'} \right)\), chỉ ra hai vectơ không cùng phương và có giá song song hoặc nằm trong mặt phẳng \(\left( {A'B'C'} \right)\).
Để xác định một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\), chỉ ra một đường thẳng vuông góc với \(\left( {A'B'C'} \right)\), sau đó chọn một vectơ có giá song song hoặc trùng với đường thẳng đó.
Lời giải chi tiết:
Ta thấy rằng \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {A'B'C'} \right)\). Suy ra \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {A'B'C'} \right)\).
Do \(ABC.A'B'C'\) là lăng trụ đứng, nên ta có \(BB' \bot \left( {A'B'C'} \right)\).
Mặt khác, vectơ \(\overrightarrow {BB'} \) có giá là đường thẳng \(BB'\), do đó \(\overrightarrow {BB'} \) là một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).
Giải mục 1 trang 32, 33 SGK Toán 12 tập 2 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 1 trang 32, 33 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo tập trung vào việc ôn tập chương 3: Đạo hàm. Đây là một phần quan trọng trong chương trình Toán 12, nền tảng cho việc giải quyết các bài toán phức tạp hơn trong các chương tiếp theo và chuẩn bị cho kỳ thi THPT Quốc gia.
Nội dung chính của Mục 1
Mục 1 yêu cầu học sinh ôn tập lại các kiến thức cơ bản về đạo hàm, bao gồm:
- Định nghĩa đạo hàm: Hiểu rõ khái niệm đạo hàm của hàm số tại một điểm và trên một khoảng.
- Các quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Đạo hàm của các hàm số thường gặp: Biết cách tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit.
- Ứng dụng của đạo hàm: Ôn tập về việc sử dụng đạo hàm để xét tính đơn điệu, cực trị của hàm số.
Giải chi tiết các bài tập trong Mục 1
Dưới đây là giải chi tiết các bài tập trong Mục 1 trang 32, 33 SGK Toán 12 tập 2 - Chân trời sáng tạo:
Bài 1: Tính đạo hàm của các hàm số sau
a) y = x3 - 2x2 + 5x - 1
Giải: y' = 3x2 - 4x + 5
b) y = sin(2x) + cos(x)
Giải: y' = 2cos(2x) - sin(x)
Bài 2: Tìm đạo hàm của hàm số y = (x2 + 1) / (x - 1)
Giải: Sử dụng quy tắc đạo hàm của thương:
y' = [(2x)(x-1) - (x2 + 1)(1)] / (x-1)2 = (x2 - 2x - 1) / (x-1)2
Bài 3: Cho hàm số f(x) = x4 - 4x2 + 1. Tìm f'(x) và các điểm cực trị của hàm số.
Giải:
f'(x) = 4x3 - 8x = 4x(x2 - 2)
f'(x) = 0 khi x = 0, x = √2, x = -√2
Lập bảng xét dấu f'(x) để xác định các điểm cực trị.
Kết luận: Hàm số có cực đại tại x = -√2 và x = √2, cực tiểu tại x = 0.
Mẹo học tập hiệu quả
Để học tốt phần đạo hàm, bạn nên:
- Nắm vững định nghĩa và các quy tắc tính đạo hàm.
- Luyện tập thường xuyên các bài tập từ cơ bản đến nâng cao.
- Sử dụng các công cụ hỗ trợ học tập như máy tính bỏ túi, phần mềm giải toán.
- Tìm hiểu các ứng dụng thực tế của đạo hàm trong các lĩnh vực khác nhau.
Tusach.vn - Đồng hành cùng bạn trên con đường học tập
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác nhất cho các bài tập trong SGK Toán 12 tập 2 Chân trời sáng tạo. Hãy truy cập tusach.vn để tìm kiếm lời giải cho các bài tập khác và nâng cao kiến thức của bạn!
| Chương | Bài | Link |
|---|---|---|
| 1 | 1 | Giải bài 1 trang 10 |
| 2 | 2 | Giải bài 2 trang 20 |