Giải bài tập 3 trang 80 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài tập 3 trang 80 SGK Toán 12 tập 2 - Chân trời sáng tạo
Bài tập 3 trang 80 SGK Toán 12 tập 2 - Chân trời sáng tạo là một phần quan trọng trong chương trình học Toán 12. Bài tập này thường tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 3 trang 80, giúp các em học sinh hiểu rõ phương pháp và tự tin làm bài.
Cho sơ đồ hình cây dưới đây.
Đề bài
Cho sơ đồ hình cây dưới đây.
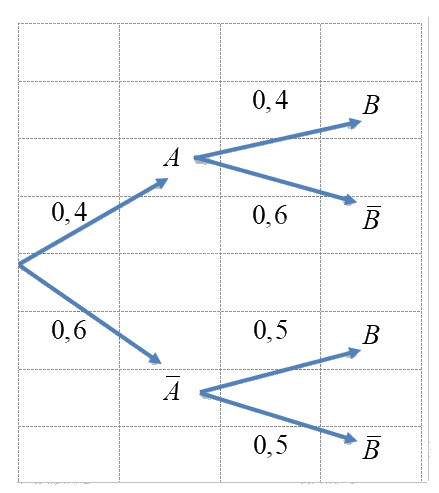
a) Xác suất của biến cố cả \(A\) và \(B\) đều không xảy ra là
A. \(0,32\)
B. \(0,4\)
C. \(0,8\)
D. \(0,92\)
b) Xác suất của biến cố \(B\) là
A. \(0,42\)
B. \(0,62\)
C. \(0,28\)
D. \(0,48\)
c) Xác suất điều kiện \(P\left( {A|B} \right)\) là
A. \(\frac{7}{{31}}\)
B. \(0,7\)
C. \(\frac{7}{{50}}\)
D. \(0,48\)
d) Giá trị của biểu thức \(\frac{{P\left( B \right)P\left( {\bar A|B} \right)}}{{P\left( {\bar A} \right)}}\) là
A. \(0,48\)
B. \(0,3\)
C. \(0,5\)
D. \(0,6\)
Phương pháp giải - Xem chi tiết
a) Xác suất cần tính là \(P\left( {\bar A\bar B} \right)\). Sử dụng sơ đồ hình cây để tính xác suất đó.
b) Xác suất cần tính là \(P\left( B \right)\). Sử dụng công thức xác suất toàn phần và sơ đồ hình cây để tính \(P\left( B \right)\).
c) Sử dụng công thức Bayes và sơ đồ hình cây để tính \(P\left( {A|B} \right)\).
d) Sử dụng sơ đồ hình cây và các câu trước để xác định giá trị của biểu thức \(\frac{{P\left( B \right)P\left( {\bar A|B} \right)}}{{P\left( {\bar A} \right)}}\).
Lời giải chi tiết
a) Dựa vào sơ đồ hình cây, xác suất của biến cố cả \(A\) và \(B\) đều không xảy ra là
\(P\left( {\bar A\bar B} \right) = 0,8.0,4 = 0,32\).
Vậy đáp án đúng là A.
b) Với công thức xác suất toàn phần, ta có
\(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\bar A} \right).P\left( {B|\bar A} \right)\).
Dựa vào sơ đồ hình cây, ta có \(P\left( A \right) = 0,2\); \(P\left( {B|A} \right) = 0,7\); \(P\left( {\bar A} \right) = 0,8\); \(P\left( {B|\bar A} \right) = 0,6\).
Do đó \(P\left( B \right) = 0,2.0,7 + 0,8.0,6 = 0,62\).
Vậy đáp án đúng là B.
c) Sử dụng công thức Bayes, ta có \(P\left( {A|B} \right) = \frac{{P\left( A \right).P\left( {B|A} \right)}}{{P\left( B \right)}}\).
Ta có \(P\left( A \right) = 0,2\); \(P\left( {B|A} \right) = 0,7\); \(P\left( B \right) = 0,62\).
Suy ra \(P\left( {A|B} \right) = \frac{{0,2.0,7}}{{0,62}} = \frac{7}{{31}}\).
Vậy đáp án đúng là A.
d) Ta có \(P\left( {A|B} \right) = \frac{7}{{31}}\), suy ra \(P\left( {\bar A|B} \right) = 1 - \frac{7}{{31}} = \frac{{24}}{{31}}\).
Ta có \(P\left( {\bar A} \right) = 0,8\). Như vậy \(\frac{{P\left( B \right)P\left( {\bar A|B} \right)}}{{P\left( {\bar A} \right)}} = \frac{{0,62.\frac{{24}}{{31}}}}{{0,8}} = 0,6\).
Vậy đáp án đúng là D.
Giải bài tập 3 trang 80 SGK Toán 12 tập 2 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài tập 3 trang 80 SGK Toán 12 tập 2 - Chân trời sáng tạo thuộc chương trình học về đạo hàm của hàm số. Đây là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Đề bài:
Cho hàm số f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
Lời giải:
- Bước 1: Tìm tập xác định của hàm số.
- Bước 2: Tính đạo hàm cấp một f'(x).
- Bước 3: Tìm các điểm làm đạo hàm bằng 0.
- Bước 4: Lập bảng biến thiên.
- Bước 5: Kết luận.
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Hàm số f(x) = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.
f'(x) = 3x2 - 6x
Giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Suy ra x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Dựa vào bảng biến thiên, ta thấy:
Lưu ý khi giải bài tập về đạo hàm:
- Luôn kiểm tra tập xác định của hàm số trước khi tính đạo hàm.
- Tính đạo hàm chính xác và cẩn thận.
- Lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến và các điểm cực trị.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể tự tin giải bài tập 3 trang 80 SGK Toán 12 tập 2 - Chân trời sáng tạo. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.
Các bài tập tương tự:
- Giải bài tập 1 trang 78 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 2 trang 79 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Các bài tập về đạo hàm khác
tusach.vn luôn đồng hành cùng các em trên con đường chinh phục kiến thức Toán học. Chúc các em học tập tốt!