Lý thuyết Tính đơn điệu và cực trị của hàm số Toán 12 Chân trời sáng tạo
Chương trình Toán 12 Chân trời sáng tạo tập trung vào việc giúp học sinh nắm vững kiến thức về hàm số, đặc biệt là các khái niệm về tính đơn điệu và cực trị. Đây là nền tảng quan trọng để giải quyết các bài toán thực tế và chuẩn bị cho kỳ thi THPT Quốc gia.
Tusach.vn cung cấp tài liệu học tập đầy đủ và chi tiết, giúp bạn hiểu rõ các định nghĩa, định lý và phương pháp giải bài tập liên quan đến chủ đề này.
Bài 1. Tính đơn điệu và cực trị của hàm số
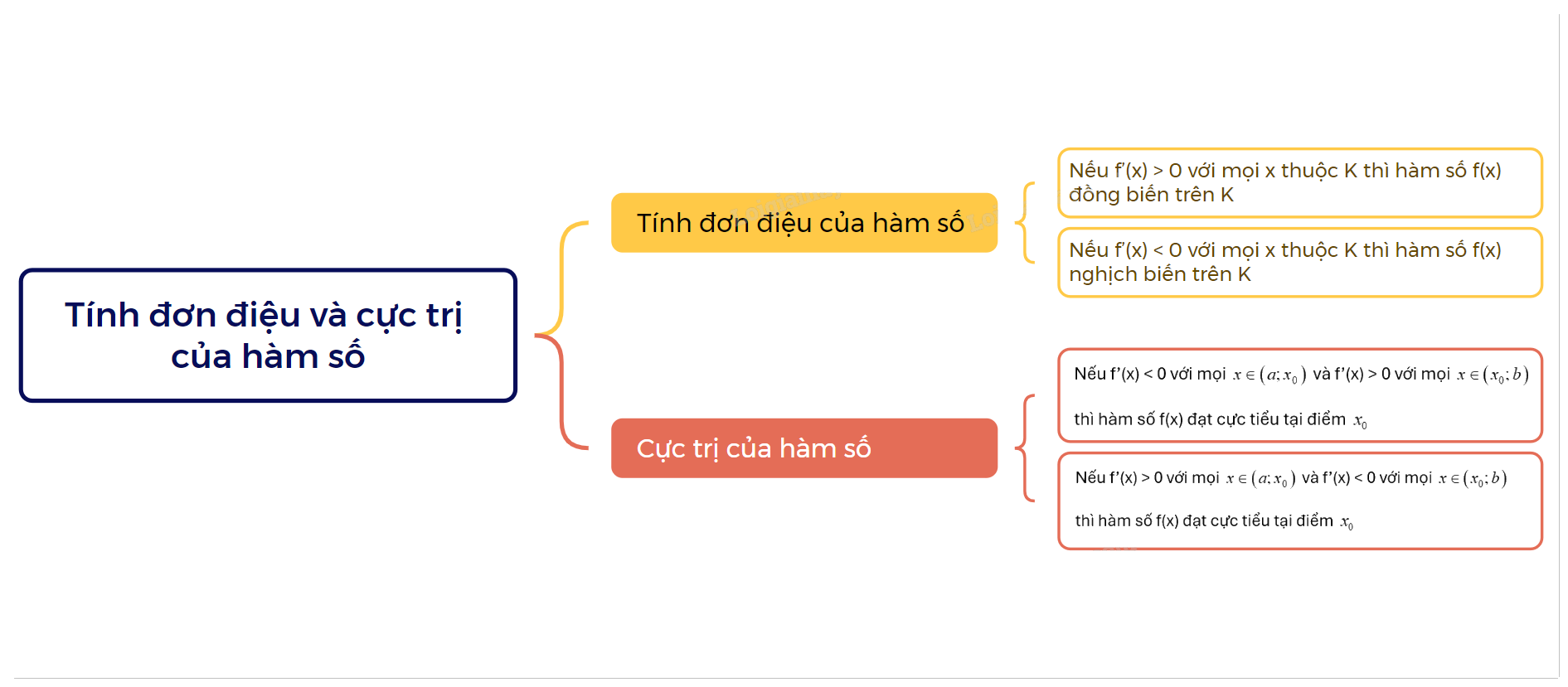
1. Tính đơn điệu của hàm số
Lý Thuyết Tính Đơn Điệu và Cực Trị của Hàm Số Toán 12 Chân Trời Sáng Tạo: Tổng Quan
Chương trình Toán 12 Chân trời sáng tạo đi sâu vào việc nghiên cứu hàm số, và một trong những phần quan trọng nhất là lý thuyết về tính đơn điệu và cực trị. Việc nắm vững kiến thức này không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng vững chắc cho các bài toán nâng cao và ứng dụng thực tế.
1. Khái Niệm Cơ Bản
- Hàm số đơn điệu: Một hàm số được gọi là đơn điệu trên một khoảng nếu nó luôn tăng hoặc luôn giảm trên khoảng đó.
- Hàm số đồng biến: Hàm số f(x) được gọi là đồng biến trên khoảng (a, b) nếu với mọi x1, x2 thuộc (a, b) và x1 < x2 thì f(x1) ≤ f(x2).
- Hàm số nghịch biến: Hàm số f(x) được gọi là nghịch biến trên khoảng (a, b) nếu với mọi x1, x2 thuộc (a, b) và x1 < x2 thì f(x1) ≥ f(x2).
- Điểm cực đại: Điểm x0 được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng mở (a, b) chứa x0 sao cho f(x0) là giá trị lớn nhất của hàm số trên khoảng đó.
- Điểm cực tiểu: Điểm x0 được gọi là điểm cực tiểu của hàm số f(x) nếu tồn tại một khoảng mở (a, b) chứa x0 sao cho f(x0) là giá trị nhỏ nhất của hàm số trên khoảng đó.
2. Điều Kiện Để Hàm Số Đơn Điệu
Để xét tính đơn điệu của hàm số, chúng ta thường sử dụng đạo hàm. Cụ thể:
- Nếu f'(x) > 0 trên một khoảng (a, b) thì hàm số f(x) đồng biến trên khoảng đó.
- Nếu f'(x) < 0 trên một khoảng (a, b) thì hàm số f(x) nghịch biến trên khoảng đó.
3. Điều Kiện Cực Trị
Để tìm điểm cực đại và cực tiểu của hàm số, ta thực hiện các bước sau:
- Tính đạo hàm cấp một f'(x).
- Giải phương trình f'(x) = 0 để tìm các điểm nghiệm.
- Xét dấu của f'(x) trong các khoảng xác định bởi các điểm nghiệm.
- Nếu f'(x) đổi dấu từ dương sang âm tại x0 thì x0 là điểm cực đại.
- Nếu f'(x) đổi dấu từ âm sang dương tại x0 thì x0 là điểm cực tiểu.
4. Ứng Dụng của Lý Thuyết
Lý thuyết về tính đơn điệu và cực trị có nhiều ứng dụng trong thực tế, ví dụ như:
- Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên một khoảng.
- Giải các bài toán tối ưu hóa.
- Nghiên cứu sự biến thiên của hàm số.
5. Bài Tập Ví Dụ
Ví dụ: Xét hàm số f(x) = x3 - 3x2 + 2. Tìm các điểm cực đại và cực tiểu của hàm số.
Giải:
- Tính đạo hàm: f'(x) = 3x2 - 6x.
- Giải phương trình f'(x) = 0: 3x2 - 6x = 0 => x = 0 hoặc x = 2.
- Xét dấu của f'(x):
| Khoảng | f'(x) | Kết luận |
|---|
| (-∞, 0) | + | Hàm số đồng biến |
| (0, 2) | - | Hàm số nghịch biến |
| (2, +∞) | + | Hàm số đồng biến |
- Kết luận: Hàm số có điểm cực đại tại x = 0 và điểm cực tiểu tại x = 2.
Kết Luận
Lý thuyết về tính đơn điệu và cực trị của hàm số là một phần quan trọng trong chương trình Toán 12 Chân trời sáng tạo. Việc nắm vững kiến thức này sẽ giúp bạn tự tin giải quyết các bài toán và ứng dụng vào thực tế. Hãy luyện tập thường xuyên và tham khảo thêm các tài liệu học tập khác để hiểu sâu hơn về chủ đề này.