Giải Bài Tập 14 Trang 67 Toán 12 Tập 2 - Chân Trời Sáng Tạo
Chào mừng bạn đến với lời giải chi tiết bài tập 14 trang 67 SGK Toán 12 tập 2, thuộc chương trình Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp bạn hiểu sâu sắc kiến thức và tự tin làm bài tập.
tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
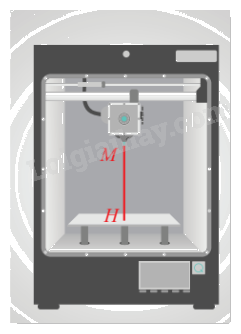
Phần mềm điều khiển máy in 3D cho biết đầu in phun của máy đang đặt tại điểm \(M\left( {3;4;24} \right)\) (đơn vị: cm). Tính khoảng cách từ đầu in đến khay đặt vật in có phương trình \(z - 4 = 0\).
Giải Bài Tập 14 Trang 67 Toán 12 Tập 2 - Chân Trời Sáng Tạo: Hướng Dẫn Chi Tiết
Bài tập 14 trang 67 SGK Toán 12 tập 2 Chân trời sáng tạo là một bài tập quan trọng, thường xuất hiện trong các đề thi. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Nội dung Bài Tập 14 Trang 67
Bài tập 14 thường xoay quanh việc tìm đạo hàm của hàm số, xét tính đơn điệu của hàm số, hoặc tìm cực trị của hàm số. Cụ thể, bài tập có thể yêu cầu:
- Tính đạo hàm f'(x) của hàm số f(x).
- Xác định khoảng đơn điệu của hàm số dựa vào dấu của f'(x).
- Tìm cực đại, cực tiểu của hàm số bằng cách giải phương trình f'(x) = 0 và xét dấu đạo hàm cấp hai f''(x).
Phương Pháp Giải Bài Tập 14 Trang 67
- Bước 1: Xác định hàm số f(x) và tập xác định của hàm số.
- Bước 2: Tính đạo hàm f'(x) của hàm số. Sử dụng các quy tắc tính đạo hàm đã học (quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp...).
- Bước 3: Tìm các điểm mà f'(x) = 0 hoặc f'(x) không xác định. Đây là các điểm nghi ngờ là cực trị của hàm số.
- Bước 4: Lập bảng biến thiên của hàm số. Xét dấu của f'(x) trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến của hàm số.
- Bước 5: Kết luận về cực đại, cực tiểu của hàm số. Dựa vào bảng biến thiên, xác định các điểm cực đại, cực tiểu và giá trị tương ứng.
Ví dụ Minh Họa Giải Bài Tập 14 Trang 67
Giả sử bài tập 14 yêu cầu tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.
Giải:
- Bước 1: Hàm số f(x) = x3 - 3x2 + 2 có tập xác định là R.
- Bước 2: f'(x) = 3x2 - 6x.
- Bước 3: f'(x) = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2.
- Bước 4: Lập bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|
| f'(x) | + | - | + |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
- Bước 5: Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Lưu Ý Khi Giải Bài Tập 14 Trang 67
- Luôn kiểm tra tập xác định của hàm số trước khi tính đạo hàm.
- Sử dụng đúng các quy tắc tính đạo hàm.
- Lập bảng biến thiên một cách cẩn thận để tránh sai sót.
- Kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số.
Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết bài tập 14 trang 67 SGK Toán 12 tập 2 Chân trời sáng tạo một cách hiệu quả. Chúc bạn học tốt!
Truy cập tusach.vn để xem thêm nhiều bài giải Toán 12 và các tài liệu học tập hữu ích khác.
