Giải bài tập 3 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài tập 3 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập 3 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo là một phần quan trọng trong chương trình học Toán 12. Bài tập này thường tập trung vào các khái niệm cơ bản về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 3 trang 18, giúp các em học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
Tìm giá trị nhỏ nhất của các hàm số sau: a) (y = {x^3} - 3x - 4) trên nửa khoảng [-3;2) b) (y = frac{{3{x^2} - 4x}}{{{x^2} - 1}}) trên khoảng (( - 1; + infty ))
Đề bài
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) \(y = {x^3} - 3x - 4\) trên nửa khoảng [-3;2) b) \(y = \frac{{3{x^2} - 4x}}{{{x^2} - 1}}\) trên khoảng \(( - 1; + \infty )\)
Phương pháp giải - Xem chi tiết
Tìm đạo hàm, lập bảng biến thiên và xác định giá trị nhỏ nhất
Lời giải chi tiết
a) Xét \(y = {x^3} - 3x - 4\) trên nửa khoảng [-3;2)
\(y' = 3{x^2} - 3 = 0 \Rightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Bảng biến thiên:
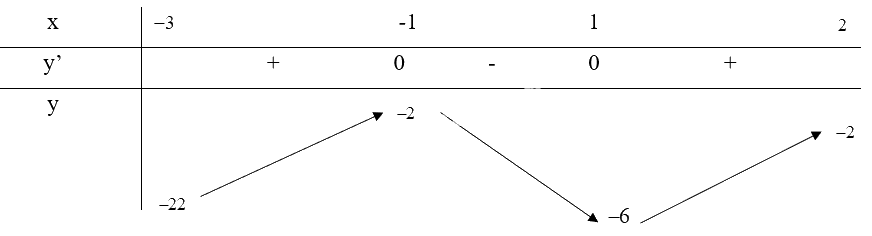
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[ - 3;2)} y = y( - 3) = - 22\), \(\mathop {\max }\limits_{[ - 3;2)} y = y( - 1) = - 2\).
b) Xét \(y = \frac{{3{x^2} - 4x}}{{{x^2} - 1}}\) trên khoảng \(( - 1; + \infty )\)
Tập xác định: \(D = ( - 1; + \infty )\)
\(y' = \frac{{4{x^2} - 6x + 4}}{{{{({x^2} - 1)}^2}}} > 0, \forall x \in D\)
Bảng biến thiên:
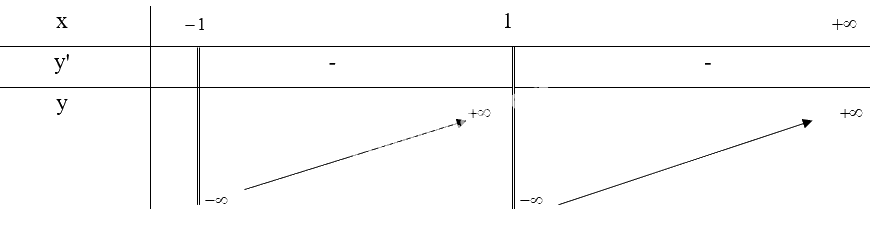
Từ bảng biến thiên, ta thấy hàm số không tồn tại giá trị nhỏ nhất trên khoảng \(( - 1; + \infty )\)
Giải bài tập 3 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài tập 3 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về đạo hàm, một trong những chủ đề quan trọng và nền tảng của Toán học lớp 12. Việc nắm vững kiến thức về đạo hàm không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là bước chuẩn bị quan trọng cho kỳ thi THPT Quốc gia.
Nội dung bài tập 3 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập 3 thường yêu cầu học sinh:
- Tính đạo hàm của hàm số tại một điểm.
- Tìm đạo hàm của hàm số.
- Áp dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số, cực trị của hàm số, và các bài toán tối ưu.
Lời giải chi tiết bài tập 3 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, Tusach.vn xin trình bày lời giải chi tiết như sau:
(Giả sử bài tập 3 là: Cho hàm số y = x3 - 3x2 + 2. Tính đạo hàm y' và tìm các điểm cực trị của hàm số.)
- Tính đạo hàm y':
- Tìm các điểm cực trị:
- Xác định loại cực trị:
- Khi x < 0: y' > 0 (hàm số đồng biến)
- Khi 0 < x < 2: y' < 0 (hàm số nghịch biến)
- Khi x > 2: y' > 0 (hàm số đồng biến)
- Tính giá trị cực đại và cực tiểu:
y' = 3x2 - 6x
Để tìm các điểm cực trị, ta giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Ta xét dấu của y' trên các khoảng:
Vậy, hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
y(0) = 2 (cực đại)
y(2) = -2 (cực tiểu)
Mẹo giải bài tập về đạo hàm
Để giải tốt các bài tập về đạo hàm, các em học sinh cần:
- Nắm vững các công thức tính đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm giải toán để kiểm tra kết quả.
- Hiểu rõ bản chất của đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
Tusach.vn – Đồng hành cùng học sinh trên con đường chinh phục Toán học
Tusach.vn luôn đồng hành cùng các em học sinh trong quá trình học tập và rèn luyện môn Toán. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết, giúp các em học sinh nắm vững kiến thức và đạt kết quả tốt nhất.
Hãy truy cập Tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu hữu ích khác!